Навигация
Сущность средней в статистике, виды и формы средних
3. Сущность средней в статистике, виды и формы средних
Средняя в статистике - обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку, определяющая уровень признака в расчете на единицу совокупности.
Виды средних
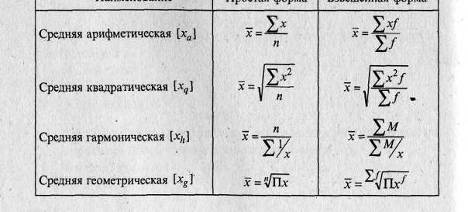
В представленных формулах применены следующие обозначения:
x - значения признака;
![]() - среднее значение признака;
- среднее значение признака;
Σ - знак суммирования;
П - знак перемножения;
f (частота) и М (произведение частоты на значения признака) - веса для расчета взвешенной средней:
N и f - численность единиц совокупности;
М - общий объем варьирующего признака.
Если средние вычислить по одним и тем же данным, то приведенные виды средних по своим численным значения встают в следующий ряд:
xh < xg < ха < хq,
иллюстрируя так называемое правило мажорантности средних.
Одна из задач определения средней состоит в правильности выбора вида средней величины.
При выборе вида средней необходимо учитывать экономическое содержание индивидуальных признаков, которое должно быть сохранено и в итоговой средней величине. При этом любые промежуточные действия, включая конечный результат, должны быть экономически значимы.
4. Средняя арифметическая и условия ее применения
Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака всей совокупности образуется как сумма значений этого признака у ее отдельных единиц.
Формулы и техника расчетов следующие:
простой средней арифметической (невзвешенной)
![]()
взвешенной средней арифметической
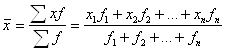
Пример 1.3.8. По данным табл. 1.6.2, повторно приведенной далее, осуществим расчет среднего производственного стажа работников, используя формулу арифметической простой (невзвешенной)
Таблица 1.6.2
Производственный стаж работников и их среднемесячная выработка изделий
| Номер работника по списку | Производственный стаж, лет | Среднемесячная выработка изделий, шт. |
| 1 | 8 | 10 |
| 2 | 2 | 6 |
| 3 | 6 | 7 |
| 4 | 1 | 6 |
| 5 | 4 | 9 |
| 6 | 2 | 8 |
| 7 | 10 | 12 |
| 8 | 5 | 10 |
| 9 | 4 | 8 |
| 10 | 3 | 7 |
| 11 | 6 | 9 |
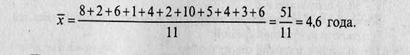
Применение арифметической средней объясняется тем, что объем варьирующего признака для всей совокупности - общее число проработанных лет работниками (51 год), образуется как сумма стажа каждого работника.
Расчет средней арифметической по данным ряда распределения имеет свои особенности. Проиллюстрируем эти особенности по данным группировки в табл. 1.3.5.
средний арифметический вариация
Таблица 1.3.5
Расчет среднего производственного стажа работников на основе ряда распределения
| Стаж, лет | Число работников, f | Середина интервала х | xf |
| 1 – 4 | 4 | 2,5 | 10,0 |
| 4 – 7 | 5 | 5,5 | 27,5 |
| 7 – 10 | 2 | 8,5 | 17,0 |
| Итого | 11 | - | 54,5 |
В данном случае следует воспользоваться формулой средней арифметической взвешенной, поскольку интервальные значения признака встречаются не один раз, и эти числа повторений (частоты) не одинаковы.
Конкретными значениями признака, которые должны непосредственно участвовать в расчетах, служат середины (центры) интервалов (но не средние в интервалах значения!), а весами - частоты:
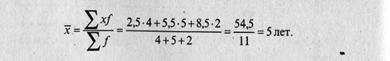
Данный результат отличается от полученного на основе средней арифметической простой. Это объясняется тем, что в расчете на основе ряда распределения мы располагаем не исходными индивидуальными данными, а лишь сведениями о величине середины (центра) интервала.
Похожие работы
... цену приобретения акций: Решение Воспользуемся для определения средней цены формулой (7): руб. В практике реальных расчетов взвешенные средние гармонические используются чаще. 4. Понятие, виды и показатели вариации Рассматривая зарегистрированные при статистическом наблюдении величины того или иного признака у отдельных единиц совокупности, обнаруживаем, что они различаются между ...
... 21 2,0 2,8 3,8 22 2,0 2,8 3,7 23 2,0 2,8 3,7 24 2,0 2,7 3,7 25 2,0 2,7 3,7 26 2,0 2,7 3,7 27 2,0 2,7 3,6 28 2,0 2,7 3,6 29 2,0 2,7 3,6 30 2,0 2,7 3,6 ¥ 1,9 2,5 3,3 ТЕСТЫ к практическому занятию по теме «Средние величины, оценка разнообразия признака в вариационном ряду. Оценка достоверности» 1. Средние величины применяются для характеристики ...
... . Величины динамического ряда принято называть уровнем ряда. Уровни динамического ряда могут быть представлены абсолютными величинами, относительными величинами (интенсивными, экстенсивными показателями), средними величинами. Динамические ряды могут быть двух видов: - моментный динамический ряд (характеризует явление на какой-то момент времени, например, число родившихся на 1.01.04) - ...
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
0 комментариев