Навигация
Виды показателей вариации
24025
знаков
12
таблиц
2
изображения
7. Виды показателей вариации
Показатели вариации являются числовой мерой уровня колеблемости признака. Одновременно по размеру показателя вариации делают вывод о типичности, надежности средней величины, найденной для данной совокупности, и об однородности самой совокупности.
Важнейшие виды показателей вариации:
1) размах вариации [R]
R = xmax - xmin
2) среднее линейное отклонение [
]
3) дисперсия [σ2]
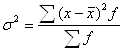
4) среднее квадратическое отклонение [σ]
5) коэффициент вариации [v]
Размах вариации учитывает только крайние значения признака и не учитывает все промежуточные.
Дисперсия не имеет единиц измерения.
Равные значения средних квадратических отклонений, рассчитанных для разных совокупностей, не позволяют делать вывод об одинаковой степени вариации.
Коэффициенты вариации позволяют сравнить степени вариации признака различных совокупностей.
Сам по себе коэффициент вариации, если его величина не превышает 33-35%, позволяет сделать вывод об относительно невысокой колеблемости признака, о типичности, надежности средней величины, об однородности совокупности. Если он более 33-35%, то все приведенные выводы следует изменить на противоположные.
Проиллюстрируем расчет показателей вариации.
Пример 1.3.12. Имеется ряд распределения (табл. 1.3.8).
Таблица 1.3.8
Распределение по стажу
| Стаж, лет | Число работников, чел. |
| 1-7 4-7 7-10 | 4 5 2 |
| Итого | 11 |
Определите:
1)размах вариации;
2)дисперсию;
3)среднее квадратическое отклонение;
4)коэффициент вариации.
Решение
1) Размах вариации - разница между максимальным и минимальным значениями признака: R= 10-1 =9 лет. Заметим, что R лучше находить по исходным несгруппированным данным, что уже сделано нами при расчете величины интервала.
Остальные показатели потребуют более трудоемких расчетов. Определим показатели вариации производственного стажа работников (табл. 1.3.9).
Таблица 1.3.9
Расчет показателей вариации производственного стажа работников
| Стаж, лет | Число работников | x | xf |
| ( | ( |
| 1-4 4-7 7-10 | 4 5 2 | 2,5 5,5 8,5 | 10,0 27,5 17,0 | -2,5 0,5 3,5 | 6,25 0,25 12,25 | 25,00 1,25 24,20 |
| Итого | 11 | - | 54,5 | - | - | 50,75 |
=54,5 / 11 = 5,0 лет
xf= 54,5 найден ранее (см. пример 1.3.8).
2) Дисперсия равна:
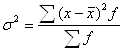=50,75 / 11 = 4,6
3) Среднее квадратическое отклонение равно:
2,1 года
4) Коэффициент вариации равен:
= (2,1 / 5,0) ´100 = 42,0%.
Анализ полученных данных говорит о том, что стаж работников предприятия отличается от среднего стажа ( = 5,0) в среднем на 2,1 года, или на 42,0%. Значение коэффициента вариации превышает 33%, следовательно, вариация производственного стажа велика, найденный средний производственный стаж плохо представляет всю совокупность работников, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по производственному стажу.
Похожие работы
... цену приобретения акций: Решение Воспользуемся для определения средней цены формулой (7): руб. В практике реальных расчетов взвешенные средние гармонические используются чаще. 4. Понятие, виды и показатели вариации Рассматривая зарегистрированные при статистическом наблюдении величины того или иного признака у отдельных единиц совокупности, обнаруживаем, что они различаются между ...
... 21 2,0 2,8 3,8 22 2,0 2,8 3,7 23 2,0 2,8 3,7 24 2,0 2,7 3,7 25 2,0 2,7 3,7 26 2,0 2,7 3,7 27 2,0 2,7 3,6 28 2,0 2,7 3,6 29 2,0 2,7 3,6 30 2,0 2,7 3,6 ¥ 1,9 2,5 3,3 ТЕСТЫ к практическому занятию по теме «Средние величины, оценка разнообразия признака в вариационном ряду. Оценка достоверности» 1. Средние величины применяются для характеристики ...
... . Величины динамического ряда принято называть уровнем ряда. Уровни динамического ряда могут быть представлены абсолютными величинами, относительными величинами (интенсивными, экстенсивными показателями), средними величинами. Динамические ряды могут быть двух видов: - моментный динамический ряд (характеризует явление на какой-то момент времени, например, число родившихся на 1.01.04) - ...
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
0 комментариев