Навигация
Оцінки істинного значення величини, що вимірюється, і точності вимірів. Ця задача подає великий практичний інтерес для метрології
16782
знака
0
таблиц
3
изображения
4 Оцінки істинного значення величини, що вимірюється, і точності вимірів. Ця задача подає великий практичний інтерес для метрології.
Нехай проведено 
незалежних однаково точних вимірів деякої фізичної величини, істинне значення 
якої невідомо. До того ж невідомо також і середнє квадратичне відхилення 
випадкових похибок вимірювання. Результати окремих вимірів 
, 
, ... , 
можна розглядати, як випадкові величини 
, 
, ... , 
, що є незалежні (виміри незалежні), мають те ж саме математичне сподівання (істинне значення величини, що вимірюється), однакові дисперсії 
(виміри однаково точні) і нормально розподілені (таке допущення підтверджується досвідом).
Отже, усі припущення, що було зроблено під час отримання довірчих інтервалів у пунктах 1 і 2, виконуються. Тому можна безпосередньо використати отримані в них формули. Іншими словами, істинне значення величини, що вимірюється, можна оцінювати по середньому арифметичному результатів окремих вимірів за допомогою довірчих інтервалів.
Середнє квадратичне відхилення випадкових похибок вимірів у теорії помилок характеризує точність вимірів (точність приладу).
Для оцінки використовують "виправлене" середнє квадратичне відхилення 
. Оскільки звичайно результати вимірів взаємно незалежні, мають одне й теж саме математичне сподівання (істинне значення величини, що вимірюється) і однакову дисперсію (у випадку однаково точних вимірів), то теорію, викладену в пункті 3, можна застосувати і для оцінки точності вимірів.
5 Інтервальна оцінка ймовірності біноміального розподілу. У підрозділі 2 у якості приклада 1 було вирішено задачу точкової оцінки ймовірності біноміального розподілу. Як точкову оцінку невідомої ймовірності 
було узято відносну частоту 
появи події (
– число появ події, – число випробувань). Було отримано математичне сподівання і дисперсію оцінки.
Тепер буде знайдено довірчий інтервал для оцінки ймовірності за відносною частотою.
Для спрощення припустимо, що кількість іспитів досить велика, а ймовірність не є близькою ні до одиниці, ні до нуля (досить, щоб обидві величини 
і 
були більше чотирьох). Тоді можна вважати, що частота події 
є випадковою величиною 
, розподіл якої є наближеним до нормального закону (у сенсі функції розподілу). Параметрами цього закону будуть 
і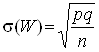 
.
Тому до випадкової величини можна застосувати відому формулу про ймовірність відхилення нормально розподіленої випадкової величини 
зі середньо квадратичним відхиленням від її математичного сподівання не більше ніж на 
, (29)
де 
– табульована функція Лапласа.
Зажадавши, щоб умова для ймовірності у формулі (29) виконувалося з надійністю 
, і, замінивши в ній на , на , на 
, а також увівши позначення 
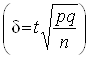, одержимо
або інакше
.
При практичному застосуванні цієї формули випадкову величину необхідно замінити невипадковою відносною частотою , що спостерігається, і підставити 
:
.
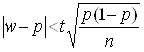Під час розв’язання цієї нерівності щодо невідомої ймовірності у припущенні 
підвищимо до квадрата обидві її частини. При цьому одержимо еквівалентну квадратну нерівність відносно :
.
Її коефіцієнт при старшому члені та дискримінант позитивні, тому її корені 
і 
дійсні, причому не дорівнюють один одному. Отже ця нерівність має розв’язання:
,
дисперсія крива розподіл сподівання
що і визначає довірчий інтервал, який слід знайти.
Аналогічний розв’язок нерівності отримуємо і у разі 
.
Похожие работы
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...
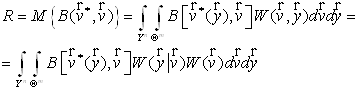
... (особливо в задачах оцінювання параметрів) за критерій якості приймають саму функцію правдоподібності. Розглянуті показники якості рішення використовують для формулювання критеріїв оптимальності рішень при розв’язанні задач обробки сигналів. 3. Критерії оптимальності рішень у задачі перевірки гіпотез Розглянемо критерії оптимальності рішень при вирішенні задач перевірки гіпотез. Байєсі ...
... інтервалу [1,36; 2,64], то можна говорити про відсутність автокореляції. Подальше проведення розрахунків за критерієм фон-Неймана та застосування методу Ейткена є недоцільним. ЗАДАЧА 4 ОЦІНКА ПАРАМЕТРІВ СИСТЕМИ ЕКОНОМЕТРИЧНИХ РІВНЯНЬ Оцінити параметри економетричної моделі, що складається з двох рівнянь: (4.1) Перше рівняння відображає залежність грошового обігу від оборотності грошей ...
... необхідності допускається застосування байєсівських процедур. Байєсівський підхід стає все більш популярним в області фармакокінетики. Можна сказати, що клінічні дослідження мають ще тривалішу історію, ніж математична статистика. Клінічні дослідження в тому розумінні, що ми звикли вкладати в це поняття, в основному одержали розвиток після другої світової війни, хоча відомі і більш ранні приклади. ...
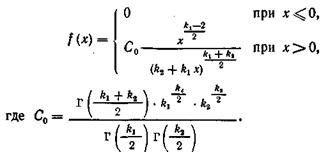
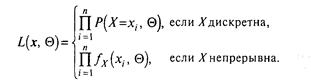
0 комментариев