Навигация
АЛГОРИТМ РАБОТЫ ПРОГРАММЫ
2. АЛГОРИТМ РАБОТЫ ПРОГРАММЫ
2.1 Структура алгоритма и данных
Задача вычисления определителя матрицы разбивается на несколько подзадач:
1) Заполнение массива начальными данными;
2) Изменение порядка матрицы по желанию пользователя и заполнение нового массива;
3) Ввод и фильтрация вводимых пользователем данных в массив;
4) Вычисление детерминанта;
4.1) Ввод исходных данных в массив
4.2) Выбор главного элемента;
4.3) Замена строк местами;
4.4) Заполнение нового массива;
4.5) Приведение матрицы к верхнему треугольному виду;
4.6) Вычисление определителя матрицы.
Согласно вышеприведенной структуре, программа будет состоять из четырех подпрограмм:
1) Подпрограмма создания формы и ввода начальных данных в массив.
В данной подпрограмме задается начальное число столбцов и строк матрицы (ее порядок), вводятся заголовки матрицы, строк и столбцов в соответствии с заданным размером.
2) Подпрограмма изменения порядка матрицы;
В данной подпрограмме формируется новая матрица, исходя из данных, введенных пользователем, вводятся новые заголовки матрицы, строк и столбцов в соответствии с заданным размером.
3) Подпрограмма фильтрации вводимых пользователем данных, при нажатии на кнопки клавиатуры;
Данная подпрограмма разрешает пользователю вводить в матрицу только цифры, разделитель дробной и целой части и знак «-». Ввод других символов запрещается. Также в этой подпрограмме производится замена неверного разделителя на верный.
4) Подпрограмма вычисления определителя.
В данной подпрограмме происходит заполнение массива данных, поочередно для каждого столбца производится выбор главного элемента (наибольшего по модулю), затем строки меняются местами и производится приведение матрицы к верхней треугольной форме, т.е. когда ниже главной диагонали содержатся только нулевые элементы. Согласно вышеприведенным формулам производится вычисление значения детерминанта и полученный результат выводится на экран.
2.2 Схема алгоритма
На рисунке 1 представлен алгоритм работы программы при возникновении события OnCreate. Процедура TForm1.FormCreate(Sender: TObject).
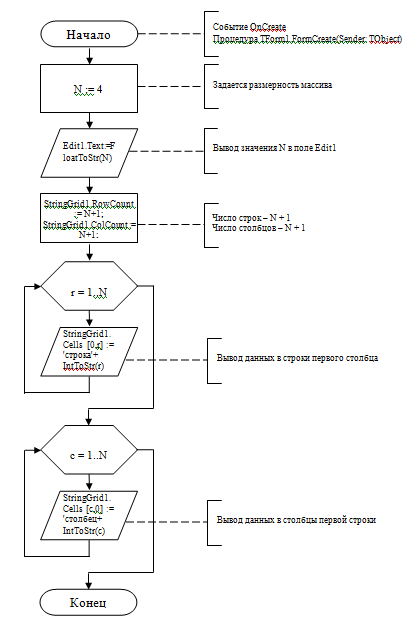
Рис. 1. Алгоритм работы программы при возникновении события OnCreate
На рисунке 2 представлен алгоритм работы программы при нажатии на кнопку «Изменить размерность массива». Процедура TForm1.Button2Click(Sender: TObject).
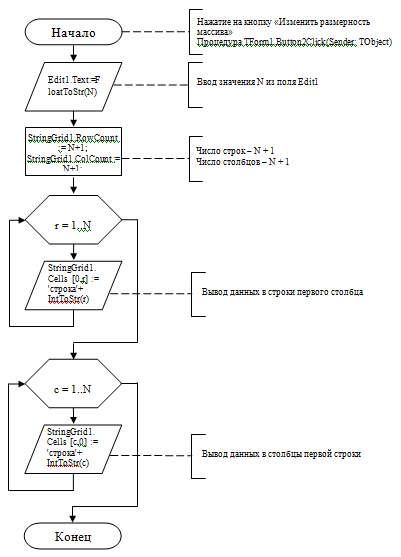
Рис. 2. Алгоритм работы программы при нажатии на кнопку «Изменить размерность массива»
На рисунке 3 представлен алгоритм работы программы при вводе данных с клавиатуры (событие OnKeyPress). Процедура TForm1.StringGrid1KeyPress(Sender: TObject; var Key: Char).
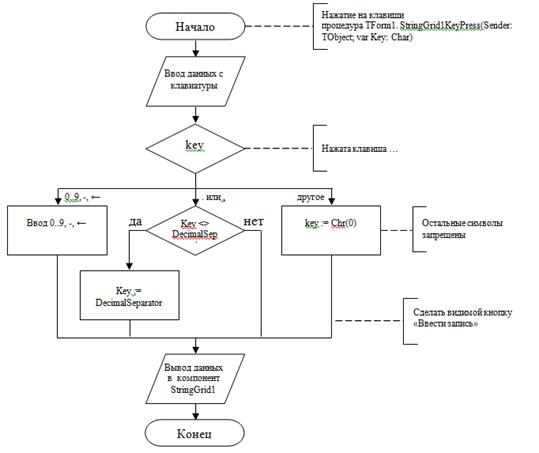
Рис. 3. Алгоритм работы программы при при вводе данных с клавиатуры (событие OnKeyPress). Процедура TForm1.StringGrid1KeyPress(Sender: TObject; var Key: Char)
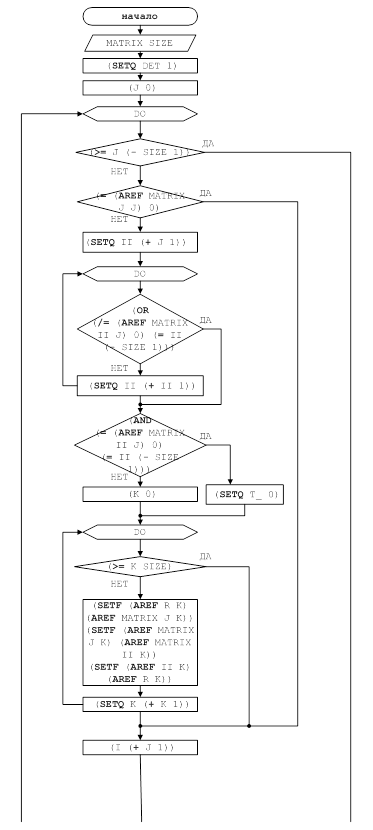
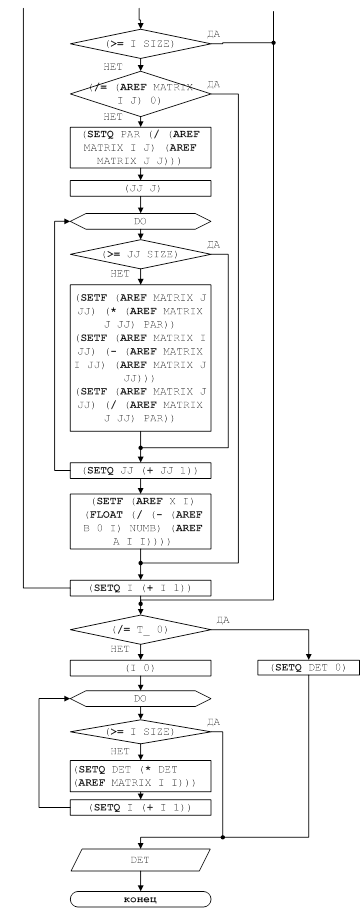
На рисунке 4 представлен алгоритм работы программы при нажатии на кнопку «Расчет». Процедура TForm1.Button1Click(Sender: TObject).
алгоритм программа pascal матрица определитель

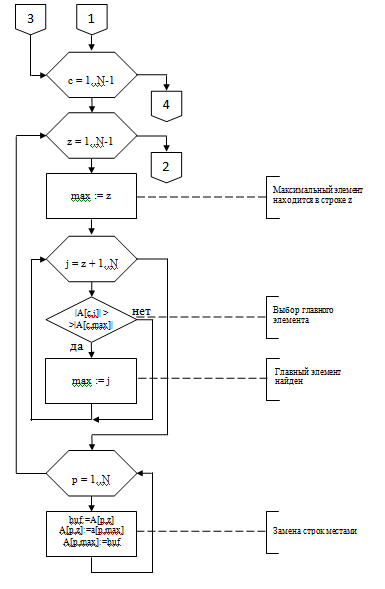

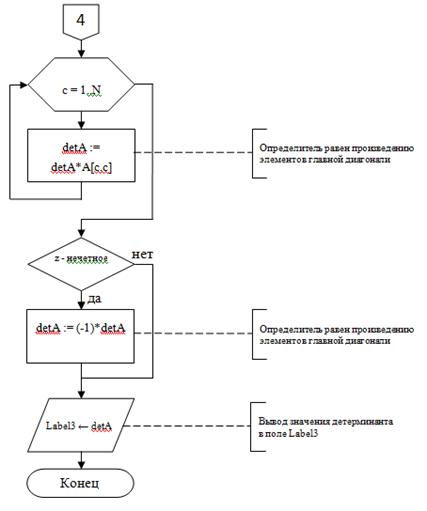
Рис. 4. Алгоритм работы программы при нажатии на кнопку «Расчет»
3. ТЕКСТ ПРОГРАММЫ
3.1 Описание переменных и структур данных
При выполнении программы используются следующие переменные: N – максимальное число строк (столбцов) массива; r, c, max, j, z, p, s, zam – номера строк и столбцов и количество производимых замен строк – все они являются переменными типа integer (целое), переменные detA, k, buf – детерминант, коэффициент и буфер, используемый при замене строк – переменные типа extended (действительное число), а также переменная А – массив, тип массива – двумерный (Massiv = array[1..Nmax,1..Nmax] of extended).
При запуске программы возникает событие «создание формы» (OnCreate), процедура TForm1.FormCreate(Sender: TObject). При этом задается количество строк и столбцов двумерного массива (по умолчанию 4 и 4) StringGrid1.RowCount := N+1; StringGrid1.ColCount := N+1; но ячейки первой строки и первого столбца не редактируемые, они используются для вывода надписей над строками и столбцами, для чего используются функции StringGrid1.Cells [0,r] := ' r = ' + IntToStr(r) и StringGrid1.Cells [c,0] := ' c = ' + IntToStr(c). Вывод данных поочередно в каждую из этих ячеек производится посредством стандартной инструкции for … to … do begin … end.
Нажатие на кнопку ![]() влечет за собой возникновение события OnClick процедура TForm1.Button2Click(Sender: TObject). Данные о количестве строк и столбцов массива считываются из поля Edit1. Так как численное значение переменной N имеет целочисленный тип для преобразования строковой записи числа, находящегося в переменной Edit1.Text в целое, используется стандартная функция N:=StrToInt(Edit1.Text).
влечет за собой возникновение события OnClick процедура TForm1.Button2Click(Sender: TObject). Данные о количестве строк и столбцов массива считываются из поля Edit1. Так как численное значение переменной N имеет целочисленный тип для преобразования строковой записи числа, находящегося в переменной Edit1.Text в целое, используется стандартная функция N:=StrToInt(Edit1.Text).
|
При нажатии на кнопку ![]() возникает событие (OnClick), процедура TForm1.Button1Click(Sender: TObject). Задаются начальные значения переменных max:= 1, detA := 1, zam:=0. Производится заполнение массива (A[c,r]:=StrToFloat(StringGrid1.Cells[c,r])), свойство StringGrid1.Cells[c,r] определяет содержимое ячейки с табличными координатами (c,r), строковые значения переменных, находящихся в ячейках (c,r) преобразуются в вещественный тип посредством стандартной инструкции StrToFloat. Стандартная инструкция for … to … do begin … end позволяет выполнять несколько раз действия, заключенные в этой инструкции. Функция abs(A[c,j]) возвращает модуль аргумента.
возникает событие (OnClick), процедура TForm1.Button1Click(Sender: TObject). Задаются начальные значения переменных max:= 1, detA := 1, zam:=0. Производится заполнение массива (A[c,r]:=StrToFloat(StringGrid1.Cells[c,r])), свойство StringGrid1.Cells[c,r] определяет содержимое ячейки с табличными координатами (c,r), строковые значения переменных, находящихся в ячейках (c,r) преобразуются в вещественный тип посредством стандартной инструкции StrToFloat. Стандартная инструкция for … to … do begin … end позволяет выполнять несколько раз действия, заключенные в этой инструкции. Функция abs(A[c,j]) возвращает модуль аргумента.
Инструкция if (stringgrid1.cells [c,r] > stringgrid1.cells [c-1,r]) and (stringgrid1.cells [c,r] < stringgrid1.cells [c+1,r]) then begin k := k+1; end; используется для выбора одного из вариантов развития программы, т.е. в случае выполнения данного условия число «особых» элементов увеличивается на 1 (k := k+1), если нет, то цикл повторяется до предпоследнего элемента матрицы. Реализует этот выбор стандартная инструкция for … to … do begin … end. Так как переменная detA действительное число, то для ее преобразования в строковый вид используется инструкция FloatToStrF(detA,fffixed,6,3). Функция zam mod 2 – проверка на четность количества замен строк, если число нечетное, то определитель умножается на -1.
Выход из программы осуществляется нажатием кнопки ![]() .
.
Похожие работы
... курсовой работы является реализация вычисления определителя методом исключения Гаусса. 1. Постановка задачи Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель. Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную ...
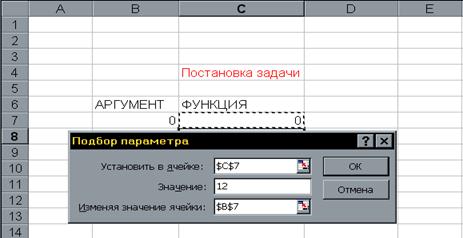
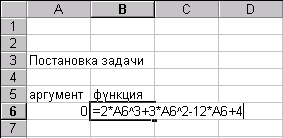
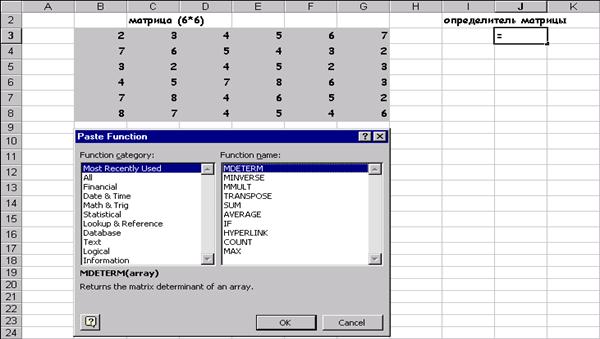
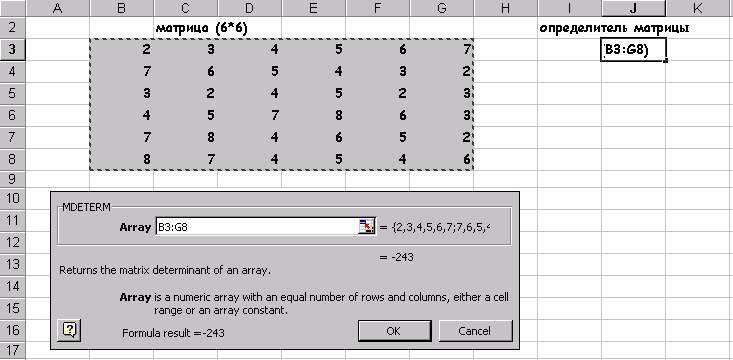
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... целевую функцию. Если до недавнего времени все четыре перечисленные выше элемента ложились на лицо принимающее решение, то теперь умение пользоваться встроенными функциями EXCEL снимает наиболее утомительный пункт, а именно, применения численных методов, и делает исследование задач принятия решения более эффективными, так как теперь для решения одной и той же более эффективными, так как теперь ...
... собственных значений сводится к проблеме раскрытия определителя по степеням и последующему решению алгебраического уравнения m- й степени. Определитель называется характеристическим (или вековым ) определителем, а уравнение (2) называется характеристическим (или вековым ) уравнением. Различают полную проблему собственных значений, когда необходимо отыскать все собственные значения ...





0 комментариев