Навигация
Численные методы и их реализация в Excel
| ||||
 | ||||

по предмету: ‘’Моделирование ’’
на тему: ‘’Численные методы и их реализация в Excel’’
Выполнила: студентка 3-курса
Камчыбекова Б.
гр. КИС-5-97
Проверил: к.т.н. профессор. Бабак В. Ф.
Бишкек – 2000
Глава 1. Подбор параметра…... 3
1.1. Нелинейные алгебраические уравнения. 3
1.2 Системы двух линейныхалгебраических уравнений. 5
Задание1. 5
Задание 2. 5
Глава 2. Матричная алгебра. 6
2.1 Определитель матрицы.. 6
2.2 Умножение матриц. 7
Задание 3. 7
Умножение на число 14. 9
Задание 4. 10
2.6 Система линейных алгебраических уравнений. 14
Задание 5. 14
Глава3. Поиск решения…... 17
1.2Оптимизация. 17
3.2Безусловный экстремум.. 17
Задание6. 18
3.4 Математическое программирование. 22
3.4.1. Линейное программирование. 23
Задание 7. 23
Задание 8. 25
Задание 9. 25
Задание 12. 27
Глава 1. Подбор параметра… 1.1. Нелинейные алгебраические уравненияПри моделировании экономических ситуаций часто приходится решать уравнение вида:
f (x, p1, p2 ,…, pn)=0 (1)
где f-заданная функция, х-неизвестная переменная.
p1, p2,…, pn – параметры модели.
Решение таких уравнений может быть как самостоятельной, так и частью более сложных задач. Как правило, исследователя интересует поведение решения в зависимости от параметров pk, k=`1,n
Решениями или корнями уравнения (1) называют такие значения переменной х, которые при подстановке в уравнение обращают его в тождество.
Только для линейных или простейших нелинейных уравнений удается найти решение в аналитической форме, т.е. записать формулу, выражающую искомую величину х в явном виде через параметры pk(например формула корней квадратного уравнения).
В большинстве же случаев приходится решать уравнение (1) численными методами, в которых процедура решения задается в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближенным, хотя может быть сколь угодно близко к точному.
Рассмотрим последовательность действий для получения решения нелинейного уравнения в среде электронной таблицы.
Пусть надо решить уравнение вида:
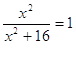 (2)
(2)
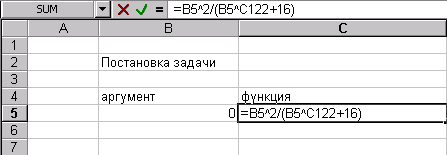
Cформируем лист электронной таблицы, как показано на рис.1. Уравнение (2) запишем в клетку С5, начиная со знака равенства, а вместо переменной x укажем адрес клктки В5, которая содержит значение начального приближения решения.
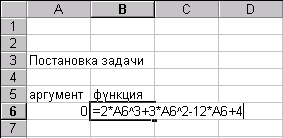
вместо переменной x укажем адрес клетки В5. которая содержит значение начального приближения решения
Метод, применяемый в EXCEL для решения таких уравнений -модифицированный конечными разностями метод Ньютона, который позволяет не сильно заботится о начальном приближении, как этого требуют другие численные методы решения уравнений (метод хорд, дихотомии и др.) Единственно, что следует учесть - это то, что будет' найдено решение ближайшее к выбранному начальному приближению.
Для получения решения уравнения (2) надо выполнить следующую последовательность действий:
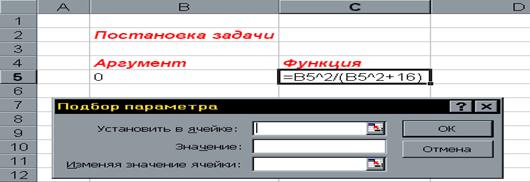
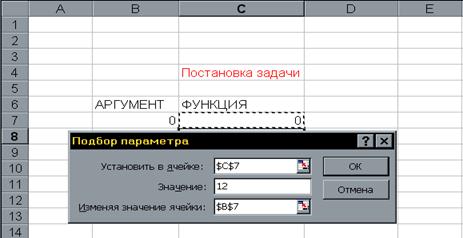
1. Выполнить команду Сервис/Подбор параметра... (получим лист электронной таблицы, как показано на Рис. 2);
2. Заполнить диалоговое окно Подбор параметра...:
2,1 Щелкнуть левой клавишей мыши в поле Установить в ячейке, после появления в нем курсора, переместить указатель мыши и щелкнуть на клетке с формулой, в нашем случае это клетка С5, абсолютный адрес которой $С$5 появится в поле рис.1
![]()
Этот адрес можно было бы набрать на клавиатуре, после появления курсора в поле. Установить в ячейке
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 7”. Режим значений — “Приложение 8”. 1.2). Проверка — сравнение результатов, полученных разными способами. Для наглядности создадим сравнительную таблицу: Математический расчет методом обратной матрицы Обращение матрицы в EXCEL x1 0,521737 0,521737318 x2 0,391105 0,391104998 x3 1,019069 1,019069651 1.3). Вывод. Сначала ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... на объем выручки оказывает также и используемые методы её определения и учета. 1.2Методы определения и учета выручки Выручка от реализации продукции (работ, услуг) может рассчитываться либо по мере отгрузки и предъявления заказчику расчетных документов либо по поступлению денежных средств на счета в коммерческих банках, а при расчетах наличными деньгами – по поступлению денежных средств в ...

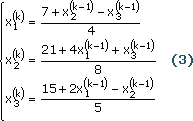
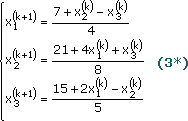



0 комментариев