Навигация
Текст программы на языке Pascal
3.2 Текст программы на языке Pascal
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids, Menus, Buttons;
type
TForm1 = class(TForm)
StringGrid1: TStringGrid;
Button1: TButton;
Edit1: TEdit;
Label1: TLabel;
Label3: TLabel;
Button2: TButton;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure StringGrid1KeyPress(Sender: TObject; var Key: Char);
private
{ Private declarations }
public
{ Public declarations }
end;
const
Nmax=10;
Type
Massiv1 = array[1..Nmax,1..Nmax] of extended;
var
Form1: TForm1;
A : Massiv1;
N, r, c: integer;
implementation
{$R *.dfm}
procedure TForm1.FormCreate(Sender: TObject);
begin
N := 4;
Edit1.Text := FloatToStr(N);
StringGrid1.RowCount := N+1;
StringGrid1.ColCount := N+1;
Label3.Caption := ' для вычисления определителя матрицы нажмите расчет';
StringGrid1.Cells [0,0] := 'Матрица А';
for r := 1 to N do begin
StringGrid1.Cells [0,r] := ' строка ' + IntToStr(r);
end;
for c := 1 to N do begin
StringGrid1.Cells [c,0] := ' столбец ' + IntToStr(c);
end;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
N:=StrToInt(Edit1.Text);
StringGrid1.RowCount:=N+1;
StringGrid1.ColCount:=N+1;
for r := 1 to N do begin
StringGrid1.Cells [0,r] := ' строка ' + IntToStr(r);
end;
for c := 1 to N do begin
StringGrid1.Cells [c,0] := ' столбец ' + IntToStr(c);
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
detA, k, buf: extended;
max, j, z, p, s, zam:integer;
begin
max:= 1;
detA := 1;
zam:=0;
for c := 1 to N do
for r := 1 to N do
A[c,r]:=StrToFloat(StringGrid1.Cells[c,r]);
for c := 1 to N-1 do begin
for z := c to N-1 do begin
max:=z;
for j := z+1 to N do begin
if abs(A[c,j]) > abs(A[c,max]) then
max:=j;
end;
for p := 1 to N do begin
buf:=A[p,z]; A[p,z]:=a[p,max]; A[p,max]:=buf;
end;
end;
for r := c+1 to N do begin
k := A[c,r]/A[c,c];
for s := 1 to N do begin
A[s,r]:= A[s,r]-A[s,c]*k;
end;
end;
if c<>max then begin
zam := zam+1;
end;
end;
for c := 1 to N do
detA := detA*A[c,c];
if zam mod 2 <> 0 then
detA := (-1)*detA;
label3.Caption := 'Детерминант матрицы равен: ' + FloatToStrF(detA,fffixed,6,3);
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
MessageDlg(Программа вычисляет детерминант (определитель) матрицы методом Гаусса с выбором главного элемента. Внимание!!! Матрица должна быть квадратной!',mtInformation,[mbOK],0);
end;
procedure TForm1.StringGrid1KeyPress(Sender: TObject; var Key: Char);
begin
case Key of
#8,'0'..'9', '-' : ;
'.',',':
begin
if Key <> DecimalSeparator then
Key := DecimalSeparator;
end;
else
key := Chr(0)
end;
end;
end.
4. ТЕСТОВАЯ ЗАДАЧА
4.1 Математическое решение задачи
В матрице вида
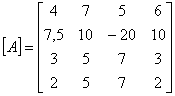
Определить детерминант.
Решение:
Вычисление определителя данной матрицы вручную целесообразно производить с помощью разложения элементов по 1-й строке по формуле (1). В итоге получится:
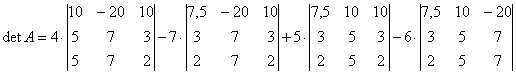 (7)
(7)
Воспользовавшись правилом Саррюса (правилом треугольников), вычисляются определители третьего порядка входящие в состав выражения (7):
detA = 4(10∙7∙2+(-20) ∙3∙5+5∙7∙10-5∙7∙10-10∙7∙3-5∙(-20) ∙2)-7∙(7,5∙7∙2+(-20) ∙3∙2+7∙3∙10-10∙7∙2-(-20)∙3∙2-7,5∙7∙3)+5∙(7,5∙5∙2+10∙3∙2+3∙5∙10-10∙5∙2-10∙3∙2-3∙5∙7,5)-6∙(7,5∙5∙7+3∙5∙(-20)+10∙7∙2-(-20) ∙5∙2-10∙3∙7-7,5∙7∙5)
detA = 4∙(140-300+350-350-210+200)-7∙(105-120+210-140+120-157,5)+5∙(75+60+150-100-60-112,5)-6∙(262,5-300+140+200-210-262,5)
detA = 4∙(-170)-7∙17,5+5∙12,5-6∙(-170)
detA = 280
Ответ: определитель матрицы равен 280
4.2 Решение, полученное с использованием разработанного программного обеспечения
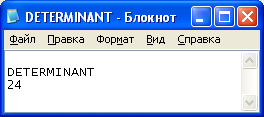
Введя исходные данные в программу получим следующий результат: «Определитель матрицы равен: 280». Результат, полученный с использованием разработанной программы соответствует результату, вычисленному математически.
Вывод: разработанное программное обеспечение верно вычисляет определитель произвольной матрицы.
5. ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЮ
Для запуска программы необходимо запустить файл Determinant.exe, дважды щелкнув по нему мышью. В появившемся окне при необходимости изменить порядок матрицы, введя значение в поле напротив надписи «Порядок матрицы» и нажав на кнопку «Изменить порядок матрицы». В ячейках таблицы ввести значения элементов матрицы. Вводимые данные должны являться действительными числами, содержать только цифры, знак « - » и разделитель целой и дробной части. После заполнения ВСЕХ элементов матрицы нажать кнопку «Расчет». Ответ будет написан под таблицей в формате: «Детерминант матрицы равен: -280,000»
Выход из программы осуществляется с помощью кнопки ![]() .
.
Внешний вид окна программы представлен на рисунке 5.
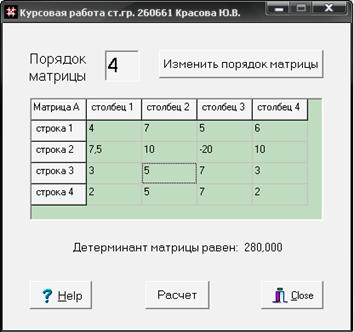
Рис. 5. Внешний вид окна программы
ЗАКЛЮЧЕНИЕ
В данной работе были изучены численные методы нахождения определителя матрицы и выбран наиболее оптимальный, с точки зрения реализации его на компьютере – метод исключения с выбором главного элемента. Написана программа с использованием массивов. Данная программа позволяет определить детерминант матрицы размером N×N, размер матрицы задается пользователем, вводимые данные – действительные числа. Вычисление определителя матрицы является второй главной задачей линейной алгебры, и применяется при решении сложных систем линейных уравнений с несколькими неизвестными.
|
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Методические указания по выполнению курсовых работ по дисциплине «программирование» для студентов дневной формы обучения, обучающихся по программе направлений подготовки бакалавров 550200, 553000, 552800. Разработал О.С. Середин, к.ф.-м.н., доцент каф. АТМ. Тула 2003 г.
2. Бахвалов Н.С., Жидков Н.П. Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2000, – 624с.
3. Волосевич А.А. Язык Object Pascal и система программирования Delphi. Учебное пособие. Минск: Белорусский государственный университет информатики и радиоэлектроники, 2003, - 61с.
4.
|
|
Похожие работы
... курсовой работы является реализация вычисления определителя методом исключения Гаусса. 1. Постановка задачи Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель. Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... целевую функцию. Если до недавнего времени все четыре перечисленные выше элемента ложились на лицо принимающее решение, то теперь умение пользоваться встроенными функциями EXCEL снимает наиболее утомительный пункт, а именно, применения численных методов, и делает исследование задач принятия решения более эффективными, так как теперь для решения одной и той же более эффективными, так как теперь ...
... собственных значений сводится к проблеме раскрытия определителя по степеням и последующему решению алгебраического уравнения m- й степени. Определитель называется характеристическим (или вековым ) определителем, а уравнение (2) называется характеристическим (или вековым ) уравнением. Различают полную проблему собственных значений, когда необходимо отыскать все собственные значения ...




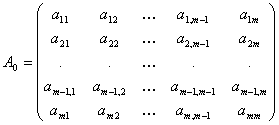
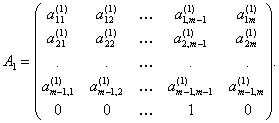

0 комментариев