Навигация
Теорема единственности для поверхностей второго порядка
4 Теорема единственности для поверхностей второго порядка
Теорема 3. Два многочлена второй степени F1(x, у, z) и F2(х, y, z) тогда и только тогда имеют одно и то же нулевое многообразие, когда они пропорциональны между собою, т. е. когда один из них получается из другого умножением на некоторое число λ≠0 .
Как н в случае многочленов от двух переменных, только одна половина этой теоремы нуждается в доказательстве: надо доказать, что два многочлена второй степени F1(x, у, z) и F2(х, y, z), имеющие одно и то же нулевое многообразие CF1 = CF2 =C, пропорциональны между собою.
Рассмотрим поверхности
F1(x, у, z)=0 (14)
и
F2(х, y, z)=0 (15)
Берем какое-нибудь направление {α: β: γ}, неасимптотическое для поверхности (14); оно будет неасимптотическим и для поверхности (15).
Диаметральная плоскость π поверхности (14), сопряженная направлению {α: β: γ}, будет и диаметральной плоскостью поверхности (15), сопряженной тому же направлению.
Возьмем теперь систему координат O'x'y'z', ось z' которой имеет направление {α: β: γ}, а две другие оси лежат в плоскости π. В этой системе координат уравнения (14) и (15) примут соответственно вид
F′1(x′, у′, z′)=a′33 z′ 2+f′1(x′, y′) = 0 (16)
F′2(x′, у′, z′)=a′33 z′ 2+f′2(x′, y′) = 0 (17)
где
f′1(x′, y′)=a′11x′ 2+ 2a′12x′y′ + a′22y′ 2+2a′1x′ + 2a′2y′ +a′0
f′2(x′, y′)=b′11x′ 2+ 2b′12x′y′ + b′22y′ 2+2b′1x′ + 2b′2y′ +b′0
Здесь a′33 ≠ 0 (и b′33 ≠ 0), в противном случае единичный вектор {0, 0, 1} оси z', удовлетворяя уравнению
φ′1(x′, у′, z′)= a′11x′ 2+ 2a′12x′y′ + a′22y′ 2+ a′33z′ 2 = 0 ,
был бы вектором асимптотического направления для поверхности (14) (соответственно для (15)) — вопреки нашим предположениям.
Нам надо доказать пропорциональность многочленов F1(x, у, z) и F2(х, y, z) т. е. пропорциональность тождественно равных им многочленов F′1(x′, у′, z′) и F′2(x′, у′, z′). Для этого обозначим через С0 пересечение множества С с плоскостью z' = 0. Множество С0 есть множество всех точек плоскости О'х'у', в которых обращается в нуль один какой-нибудь (и, следовательно, любой) из многочленов f′1(x′, y′), f′2(x′, y′). Другими словами, это есть (лежащее в плоскости О'х'у') нулевое многообразие каждого из этих многочленов.
Возможны следующие случаи:
1° Множество С0 пусто. Этот случай осуществляется тогда и только тогда, когда какое-нибудь (н тогда каждое) из равенств f′1(x′, y′)=0, f′2(x′, y′)=0 противоречиво, т. е. когда одни какой-нибудь (и тогда каждый) из многочленов f′1(x′, y′), f′2(x′, y′) тождественно равен отличной от нуля постоянной а'0, соответственно b0'„.
2° Множество совпадает со всей плоскостью О'х'у'. Это происходит тогда и только тогда, когда один какой-нибудь (и тогда каждый) из многочленов f′1(x′, y′), f′2(x′, y′) тождественно равен нулю.
3° Ни один из случаев 1°, 2° не имеет места. Тогда множество С0 есть множество всех точек кривой второго порядка, определяемой в плоскости О'х'у' каждым из уравнений
f′1(x′, y′)=0, f′2(x′, y′)=0 . (18)
В этом случае в силу теоремы единственности для многочленов второй степени от двух переменных имеем f′2(x′, y′) = μ f′1(x′, y′) при некотором μ≠0. Полагая λ=z′33: a′33 (что возможно, так как a′33≠0 ), можем написать
F′1(x′, у′, z′) = a′33z′ 2+ f′1(x′, y′),
F′2(x′, у′, z′) =λ a′33z′ 2+μ f′2(x′, y′),
Для того чтобы доказать в случае 3° пропорциональность многочленов F′1(x′, у′, z′) и F′2(x′, у′, z′), надо только показать, что μ = λ.. Так как многочлен f′1(x′, y′), не равен тождественно постоянной, то существуют значения x′=x′1, у' = у'1, для которых f′1(x′1, у'1). Найдя такие значения, решаем относительно z' уравнение
F′1(x′1, у′1, z′1) = a′33z′ 2+ 1 = 0
Получаем z′1 = (1 : a′33 )0,5. Итак, точка M1 = (x′1, у′1, z′1) принадлежит множеству С. Следовательно,
F′2(x′1, у′1, z′1) = λa′33(1 : a′33) + μ 1 = 0 , т. е. μ = λ.
Итак, в случае 3° утверждение теоремы 3 доказано. В случае 2° имеем
F′1(x′, у′, z′)= a′33 z′ 2 , a′33 ≠0,
F′2(x′, у′, z′)= b′33 z′ 2 , b′33 ≠0
и, следовательно, полагая λ=(b′33 : a′33) , имеем F′2(x′, у′, z′)=λ F′1(x′, у′, z′) — утверждение теоремы 2 верно и в этом случае.
Наконец, в случае 1° уравнения (16′), (17') принимают вид
F′1(x′, у′, z′)= a′33 z′ 2+a′0 , a′0 ≠0
F′2(x′, у′, z′)= b′33 z′ 2+b′0 , b′0 ≠0
Для того чтобы эти уравнения были эквивалентны, очевидно, необходимо и достаточно, чтобы было b′33 = λa′33 , b′0 = λa′0 при λ= (b′33 : a′33 )
Теорема 3 доказана во всех случаях.
Список литературы
1. Александров П.С. Лекции по аналитической геометрии. Наука, 1968
2. Анастасян Л.С. Геометрия. Просвещение, 1973. ч 1
3. Анастасян Л.С. Геометрия. Просвещение, 1987. ч 2
4. Базылев В.Т. Геометрия. М. , 1974. ч 1
5. Ефимов Н.В. Квадратичные формы и матрицы. Наука, 1967
6. Парнасский И.В. Многомерные пространства. Квадратичные формы и квадратики. Просвещение, 1978.
7. Погорелов А.В. Аналитическая геометрия. Наука, 1968
Похожие работы
... и увеличить объемы потребления до максимально возможных значений и платить при этом все возрастающую с ростом дохода цену. Равновесные кривые для товаров, не являющихся предметами повседневного спроса Случаи равновесных кривых для товара повседневного спроса определяются месторасположением линии максимальных объемов поверхности спроса и поверхности предложения. Для товаров, которые не являются ...
... . С расширением замкнутого объема электрические массы вещества расходятся относительно друг друга, образуется свободное пространство. Становится возможным взаимное перемещение масс, перераспределение их плотности. 4. Единая теория поля 4.1. Электромагнитные колебания В пространстве-времени, образованном гравитационными массами одного знака, электрическое поле равно нулю, вещество электрически ...
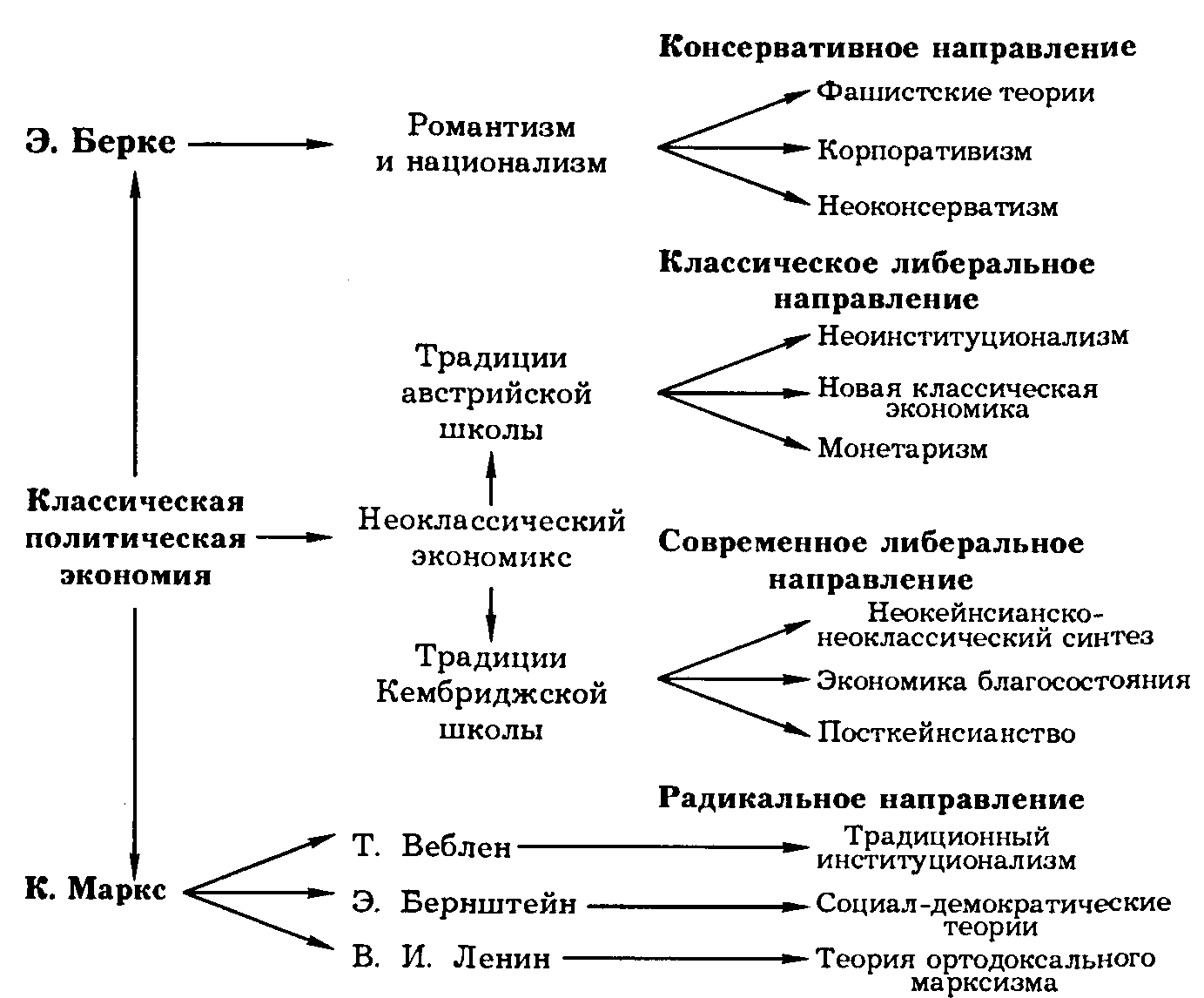
... М. В. Неоклассическая модель чистой монополии. М.: ИМЭМО, АН СССР, 1990. 3. Лейбенстайн X. Аллокативная эффективность в сравнении с "Х-эффективностью" // Теория фирмы. С. 477—506. 4. Маленво Э. Лекции... Гл. III. § 9. С. 80—85. 5. Робинсон Дж. Экономическая теория... Гл. 3—5. С. 88—130. 6. Стиглер Дж. Совершенная конкуренция: исторический ракурс // Теория фирмы. С. 299—328. 7. Самуэльсон П. ...
... производства необходимо остановиться на понятиях технического и технологического прогресса. Мы будем предполагать технологию неизменной, и пока технология неизменна, мы находимся в рамках микроэкономики K/L – капиталовооруженность. В рамках заданной технологии она может быть повышена (А ––> В). Мы как бы заменяем капиталом труд (механизация). Такие перемещения по изокванте ...
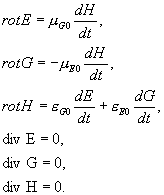
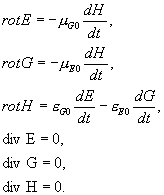



0 комментариев