Розвязування раціональних нерівностей вищих степенів методом інтервалів

2.1 Розвязування раціональних нерівностей вищих степенів методом інтервалів

Будемо розглядати розв’язання раціональних нерівностей методом інтервалів. Існують різні схеми реалізації цього методу. Розглянемо одну з цих схем, допускаючи, що розв’язується нерівність . У випадку нерівності  ця схема аналогічна.

1.Перенести всі члени нерівності вліво:

.

2.Ліву частину отриманої нерівності привести до спільного знаменника:

.

3.Багаточлени  і  розкласти на множники. Якщо при цьому з’являються однакові множники, то треба замінити їх відповідним степенем. Наприклад,

.

При скороченні треба мати на увазі, що:

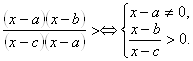
4. Виключити з розкладення нелінійні множники. Це виключення виконується таким чином.

Якщо в розкладенні є множник, , де , то його виключення залежить від знака старшого коефіцієнта і виконується за правилом:

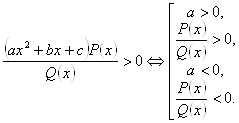
Якщо в розкладенні є множник , то його виключення здійснюється за правилами

 

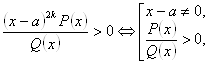
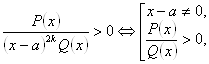
Нелінійний множник  виключається за правилом:

.

5. На числовій осі відмітимо точки, в яких обертаються в нуль всі множники, що стоять в чисельнику і знаменнику лівої частини нерівності, отриманої в результаті виконання пунктів «1» - «4». При цьому, якщо нерівність нестрога, точки, які відповідають множникам чисельника будемо визначати зафарбованими кружками, а точки, що відповідають множникам знаменника світлими. Якщо нерівність строга, всі точки відмічаються світлими кружками.

6. Поставити знаки в кожному проміжку, на якій числова вісь розбивається відміченими точками.

Спочатку поставити знак у самому правому проміжку на числовій осі за правилом: знак «+» ставиться, якщо число множників виду  парне, і знак «-», якщо це число непарне. Знаки в інших проміжках ставляться з урахуванням того, що вони чергуються в сусідніх проміжках.

7. Вибираються проміжки, в яких стоїть знак «+», якщо нерівність, отримана в пункті 4 має вигляд: , або «-», якщо ця нерівність має вигляд . Ці проміжки містять у собі крайні точки, відмічені на числовій осі зафарбованими кружками, і не містять точок, відмічених світлими кружками,. Об’єднання цих проміжків і є множиною розв’язків даної нерівності.[4:124]

Приклад 1. Розв’язати методом інтервалів нерівність

. (1)

Розв’язування:З нерівності  знаходимо ОДЗ:

 

Далі замість нерівності (1) розв’язуємо рівняння

 або  звідки

Наносимо відповідні точки на числову вісь (див. рисунок).

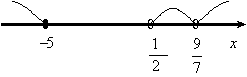
Розглядаємо кожний з утворених інтервалів окремо.

1. Підставляємо значення  з інтервалу  у нерівність (1). Дістаємо нерівність , яка не виконується. Тому нерівність (1) не виконується в усіх точках інтервалу .

2. Підставляючи в нерівність (1) значення  з інтервалу , дістаємо правильну нерівність . Отже, нерівність (1) виконується на інтервалі .

3. Підставляючи в (3) значення  з інтервалу  дістаємо неправильну нерівність . Це означає, що нерівність (1) не виконується ні в одній точці інтервалу .

Остаточно маємо розв’язок нерівності (1)

Відповідь.[1:161]

Приклад 2. Розв’язати нерівність

Розв’язування: Для знаходження коренів рівняння  необхідно розкласти його на множники. Отже

Отже числа,, є коренями даного рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

 на одному з інтервалів. Зокрема, взявши точку  з інтервалу , дістаємо . Провівши «криву знаків», визначаємо знак  в кожному з інтервалів.

 +  +

1 2 3 x

Відповідь:

 

2.2 Розв’язування раціональних нерівностей вищих степенів узагальненним методом інтервалів

Нехай потрібно розв'язати нерівність

,

де  цілі додатні числа;

— дійсні числа, серед яких немає рівних і такі, що . Нерівності подібного типу розв'язують із застосуванням узагальненого метода інтервалів. В основі цього метода лежить така властивість двочлена  точка  ділить числову вісь на дві частини, причому якщо  (- парне), то вираз  праворуч і ліворуч від точки  зберігає додатний знак; якщо  (- непарне число), то вираз  праворуч від точки  додатний, а ліворуч від точки  від'ємний.

Для розв'язання нерівності

узагальненим методом інтервалів на числову вісь наносимо числа ; в проміжку праворуч від найбільшого з них ставимо знак «плюс», а потім, рухаючись справа наліво, при переході через чергове число  змінюємо знак, якщо  — непарне число, і зберігаємо знак, якщо.  — парне число.

Зауваження 1. Якщо зустрічаються вирази , то праворуч від найбільшого з  не обов'язково буде знак « + ». У цьому випадку найкраще визначити знак лівої частини нерівності в якомусь з інтервалів, а потім поставити знаки в кожному з інтервалів з урахуванням викладених вище міркувань.

Зауваження 2. Наведені вище міркування справедливі і для нерівностей виду

, , , де

.

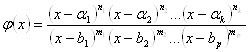Приклад 1. Розв’язати нерівність

Перепишемо нерівність у рівносильному вигляді

Числа , , ,  є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

 

на одному з інтервалів. Зокрема, взявши точку  з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» з урахуванням того, що ліворуч і праворуч точки  буде той самий знак «+», тому що у виразі  показник степеня (число 4) є числом парним.

 

 +  + +

-7 - 6 x

Відповідь:.

 

Приклад 2. Розв’язати нерівність

Числа ,, є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції  на одному з інтервалів. Зокрема, взявши точку  з інтервалу , дістаємо . Провівши «криву знаків» з урахуванням того, що ліворуч і праворуч точки  і  буде той самий знак «-», тому що у виразах і (х + 3)⁶  показник степеня (число 4 і 6 відповідно) є парні числа, визначаємо знак f(x) в кожному з інтервалів.

 

  +

-3 1 5 x

Відповідь: .

Приклад 3. Розв’язати нерівність

Числа, ,  є коренями рівняння Наносимо дані точки на числову вісь. Оскільки дискримінант квадратного тричлена х², то для всіх  і, значить, парабола  не перетинає вісь Ох. За допомогою «кривої знаків» дістаємо розв’язання.

 +  +

-1 1 2 x

Відповідь: .

 

Приклад 4. Розв’язати нерівність

Числа , ,  є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції  на одному з інтервалів. Зокрема, взявши точку  з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.

 +  +

-3 -1 0 x

Відповідь:..

Приклад 5. Розв’язати нерівність

.

Перепишемо нерівність

.

Числа, ,  є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції

 

на одному з інтервалів. Зокрема, взявши точку  з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.

 +  + +

- 6 x

 

Відповідь:.