Розв’язування дробово-раціональних нерівностей

2.3 Розв’язування дробово-раціональних нерівностей

 

Приклад 1. Розв’язати нерівність

.

Розв’язання: розкладемо чисельник і знаменник дробу, що стоїть в лівій частині нерівності, на множники:

.

Отриманий дріб містить два нелінійні множники:  і . Перший з них додатний і його можна опустити, другий множник виключимо у відповідності з пунктом 4:

Далі, на числовій осі відмітимо точки ,  та інтервали, що утворюються при цьому, знаками:

 + +

-2 2 x

Виберемо інтервал  відмічений знаком «-» (так як ), і нанесемо на числову вісь точку . Ця точка попадає у вибраний інтервал. «Виколюючи» точку , отримуємо інтервали  і , об’єднання яких утворює множину розв’язків даної нерівності:

Відповідь: .

Приклад 2. Розв’язати нерівність

.

Розв’язання: розкладемо багаточлен, що стоїть в чисельнику лівої частини нерівності, на множники. Розглянемо рівняння . Серед дільників 8 підберемо корінь рівняння . Розділимо ліву частину рівняння на двочлен :

 

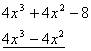
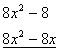
Тепер розглянемо рівняння . Серед дільників 8 підберемо рівняння  і розділимо ліву частину на двочлен :

 

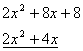
Так як квадратний тричлен  не має дійсних коренів, отримаємо розкладення

.

Таким чином, дана нерівність перетворюється до вигляду:

.

Дріб в лівій частині цієї нерівності містить два нелінійних множники: квадратний тричлен , що більший нуля, і . Виключимо ці множники:

На числовій осі відмітимо точки ,  і інтервали, що утворюються знаками:

Виберемо інтервал  зі знаком «-» і потім відмітимо на осі точку . Ця точка належить вибраному інтервалу, і тому, виключаючи цю точку, отримуємо, що  - множина розв’язків даної нерівності.

Відповідь: .

Приклад 3. Розв’язати нерівність

.

Розв’язання: у відповідності з описаною схемою методу інтервалів

Будемо відмічати на числовій осі точки , ,  зафарбованими кружками (нерівність нестрога!), а точку  - світлим кружком:

Розв’язок даної даної нерівності складаються з об’єднанням проміжків .

Відповідь: .

 

Приклад 4. Розв’язати нерівність

.

Розв’язування: Нанасимо на числову пряму точки , , , , . Точки , ,  відзначаємо темними кружками, а точки ,  світлими.

Провівши «кривину знаків» з урахуванням того, що в околі точок  і  ліва частина нерівності зберігає знак (тому що у виразах ),  показники степенів є парними числами), дістанемо розв’язання Ця множина на рисунку заштрихована.

Відповідь:

Приклад 5. Розв’язати нерівність

.

Наносимо точки  числову вісь. За допомогою «кривої знаків» дістанемо розв’язки, заштриховані на рисунку.

Зазначимо, що точка  входить у множину розв’язків, тому що при  дістанемо .

Відповідь: .