Основи методу квадратур

3.5.2 Основи методу квадратур

Передавальну функцію еквівалентного об'єкта керування  ідентифікуємо до рівняння другого порядку.

Уведемо заміну , де  - частота і запишемо передавальну функцію  таким чином:

,

де  - поліноми ДЧХ;  - поліноми УЧХ.

Вираз для дійсної частотної характеристики запишемо у вигляді

,

де  - доповнюючий поліном.

Відношення поліномів в останньому рівнянні можна привести до такої форми , де  - відношення поліномів ДЧХ. Тоді ДЧХ приймає вигляд

.

Уявна частотна характеристика , де  - відношення поліномів УЧХ.

З врахуванням вищевикладеного передавальна функція  приводиться до вигляду . Тепер задача полягає в тому, щоби знайти значення множників  і . Множник  знаходиться при . Тоді . Множник  знаходиться при . Тоді , де  - частота переходу ДЧХ через частотну вісь. При таких умовах еквівалентна передавальна функція об'єкта керування приймає вигляд

або ,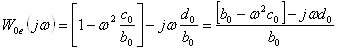

де  - визначаються з функції , а  - з функції .

Якщо позначити , то приходимо до наступного рівняння

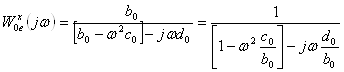
або .

Таким чином, передавальну функцію  можна отримати з наступного диференціального рівняння відносно вхідної величини

.

Для лінійної системи виконується принцип суперпозиції, тобто . Тоді отримуємо аналогічне диференціальне рівняння для вихідної величини:

.

Характер перехідного процесу залежатиме від відношення постійних часу .

При  перехідний процес буде аперіодичним, який розраховується за формулою

,

де  - корені характеристичного рівняння:

.

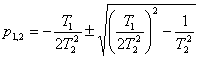При  перехідний процес буде коливальним, який розраховується за формулою

,

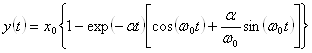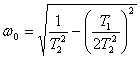де  - ступінь загасання;  - власна частота коливань.

Рівняння для передавальної функції еквівалентного об'єкта керування запишемо в такій формі

;

змішувальний установка система керування

Або

,

де ; .

Розрахуємо перехідний процес методом квадратур.

Знайдемо доповнюючий поліном для ДЧХ

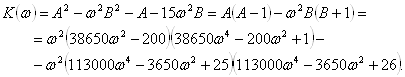
Знайдемо відношення

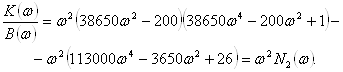
Знаходимо рівняння для дійсної частотної характеристики

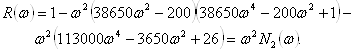
За останнім рівнянням розраховуємо ДЧХ і знаходимо частоту переходу . Графік ДЧХ показаний на рис. 6. З графіка видно, що частота переходу .

Підставивши частоту  в рівняння

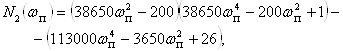
знаходимо постійну часу .

Уявна частотна характеристика має вигляд

,

звідки  

або

.

З останнього рівняння при  отримуємо: .

Рис. 6. ДЧХ еквівалентного об'єкта керування.

Таким чином, ідентифіковане характеристичне рівняння еквівалентного об'єкта керування має вигляд: , а диференціальне рівняння -  Знайдемо відношення постійних часу еквівалентного об'єкта керування: . Так як відношення постійних часу менше 2, то робимо висновок, що перехідний процес еквівалентного об'єкта керування матиме коливальний характер. Тому розрахунок перехідного процесу виконаємо за формулою

.

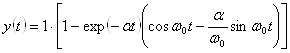Знайдемо ступінь загасання перехідного процесу об'єкта: , а власну частоту коливань за формулою

.

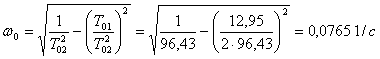Рис. 7. Графік перехідного процесу еквівалентного об'єкта керування

Тоді рівняння перехідного процесу приймає вигляд

.

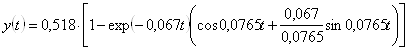Графік перехідного процесу еквівалентного об'єкта керування показаний на рис. 7.