Навигация
Явление переноса. Общее уравнение переноса
1.3 Явление переноса. Общее уравнение переноса
Группа явлений, обусловленных хаотическим движением молекул и приводящих при этом к передаче массы, кинетической энергии и импульса, называется явлением переноса.
К ним относят диффузию – перенос вещества, теплопроводимость – перенос кинетической энергии и внутреннее трение – перенос импульса.
Общее уравнение переноса, описывающее эти явления, можно получить на основе молекулярно-кинетической теории.
Пусть через площадку площадью «S» (рисунок) переносится некоторая физическая величина в результате хаотического движения молекул.
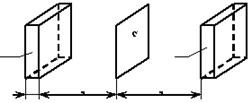
На расстояниях, равных средней длине свободного пробега ![]() , вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины «l» (l <<
, вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины «l» (l << ![]() ). Объем каждого параллелепипеда равен
). Объем каждого параллелепипеда равен
V = S l.
Если концентрация молекул равна «п», то внутри выделенного параллелепипеда имеется «S l п» молекул.
Все молекулы из-за их хаотического движения можно условно представить шестью группами, каждая из которых перемещается вдоль или против направления одной из осей координат. То есть в направлении, перпендикулярном площадке «S», перемещается ![]() молекул. Так как объем «1» находится на расстоянии
молекул. Так как объем «1» находится на расстоянии ![]() от площадки «S», то эти молекулы достигнут ее без соударения. Такое же число
от площадки «S», то эти молекулы достигнут ее без соударения. Такое же число ![]() молекул достигнет площадки «S» слева.
молекул достигнет площадки «S» слева.
Каждая молекула способна перенести некоторую величину «Z» (масса, импульс, кинетическая энергия), а все молекулы - ![]() или
или ![]() , где H = n Z – физическая величина, переносимая молекулами, заключенными в единичном объеме. В результате сквозь площадку «S» из объемов 1 и 2 за промежуток времени «Dt» переносится величина
, где H = n Z – физическая величина, переносимая молекулами, заключенными в единичном объеме. В результате сквозь площадку «S» из объемов 1 и 2 за промежуток времени «Dt» переносится величина
![]() . (1)
. (1)
Чтобы определить время «Dt», предположим, что все молекулы из выделенных объемов движутся с одинаковыми средними скоростями![]() . Тогда молекулы в объеме 1 или 2, дошедшие до площадки «S», пересекают ее в течение промежутка времени
. Тогда молекулы в объеме 1 или 2, дошедшие до площадки «S», пересекают ее в течение промежутка времени
![]() . (2)
. (2)
Разделив (1) на (2), получим, что переносимая за интервал времени «Dt» величина равна
![]() (3)
(3)
Изменение величины «Н» на единице длины «dx» ![]() называют градиентом величины «Н». Так как (Н1 – Н2) – изменение «Н» на расстоянии, равном 2
называют градиентом величины «Н». Так как (Н1 – Н2) – изменение «Н» на расстоянии, равном 2![]() , то
, то
![]() , или
, или ![]() . (4)
. (4)
После подстановки (4) в (3) и умножения полученного уравнения на время найдем поток непереносимой физической величины «Н» за промежуток времени «Dt» сквозь площадь «S»:
![]() (5)
(5)
Это общее уравнение переноса, используемое при изучении диффузии, теплопроводимости, вязкости.
1.4 Диффузия. Пассивный перенос неэлектолитов через биомембраны, уравнение Рика. Транспорт неэлектролитов через мембраны путем простой и облегченной (в комплексе с переносчиком) диффузии
Диффузия – это процесс, который приводит к самопроизвольному уменьшению градиентов концентраций в растворе, пока не установится однородное распределение частиц. Процесс диффузии играет важную роль во многих химических и биологических системах. Именно диффузией, например, определяется в основном доступ двуокиси углерода к активным фотосинтетическим структурам в хлоропластах. Для понимания особенностей транспорта растворенных молекул через клеточные мембраны необходимы детальные сведения о диффузии. Рассмотрим некоторые основные принципы диффузии в растворах.
Представим себе сосуд, в левой части которого находится чистый растворитель, а в правой – раствор, приготовленный с тем же растворителем. Пусть сначала эти две части сосуда разделены плоской вертикальной стенкой. Если теперь убрать стенку, то вследствие беспорядочного движения молекул во всех направлениях граница между раствором и растворителем будет смещаться влево до тех пор, пока вся система не станет однородной. В 1855 году Рик, изучая диффузионные процессы, обнаружил, что скорость диффузии, то есть число молекул растворенного вещества «п», пересекающих вертикальную плоскость в единицу времени, прямо пропорционально площади сечения «S» и градиенту концентрации ![]() . Таким образом,
. Таким образом,
![]()
где D – коэффициент диффузии (измеряется в м2/с в «СИ»). Знак минус указывает на то, что диффузия идет из области высокой концентрации в область низкой концентрации. Это означает, что градиент концентрации в направлении диффузии отрицателен. Уравнение (1) известно под названием первого закона диффузии Рика. Физические законы представляют собой интуитивные заключения, которые нельзя вывести из более простых утверждений и следствия из которых не противоречат эксперименту. К числу таких заключений относятся законы механики и термодинамики; таков же и закон Рика.
Рассмотрим теперь процесс диффузии несколько подробнее. Выделим в пространстве элемент объема «S × dx», как показано на рисунке
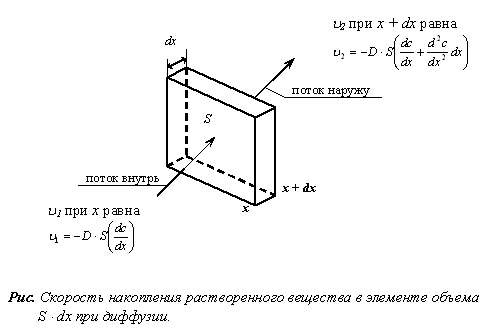
Скорость, с которой молекулы растворенного вещества входят в элемент объема через сечение «х», равна ![]() Скорость изменения градиента концентрации по мере изменения «х» равна
Скорость изменения градиента концентрации по мере изменения «х» равна
![]()
Поэтому скорость, с которой молекулы растворенного вещества покидают элемент объема через сечение, удаленное от первого на «dx», равна
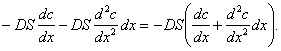
Скорость накопления молекул растворенного вещества в элементе объема представляет собой разность этих двух величин:
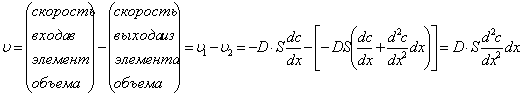
Однако та же самая скорость накопления частиц равна ![]() , так что можно написать
, так что можно написать
![]() или
или ![]()
![]() (6)
(6)
Уравнение (6) под названием уравнения диффузии или второго закона диффузии Рика, из которого следует, что изменение концентрации во времени на некотором расстоянии «х» от начальной плоскости пропорционально скорости изменения градиента концентрации в направлении «х» в момент «t».
Для решения уравнения (6) требуется использовать специальные методы (разработанные Рурье), описание которых опускаем, получаемый результат имеет простой вид:
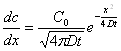 (7)
(7)
где С0 – исходная концентрация вещества в точке начала отсчета в нулевой момент времени.
По уравнению (7) можно построить график зависимости градиента концентрации ![]() от координаты «х» при различных временах «t». Оптическими методами (например, путем измерения показателя преломления) можно определить градиенты концентрации на различных расстояниях от границы, по которой началась диффузия.
от координаты «х» при различных временах «t». Оптическими методами (например, путем измерения показателя преломления) можно определить градиенты концентрации на различных расстояниях от границы, по которой началась диффузия.
Похожие работы
... материалы хорошо описываются в рамках квантово-механической фононной Модели строения и функционирования клеточных мембран, что позволяет утверждать: “ФОНОН – КВАНТ биологической (клеточной) мембраны”. Модель пригодна для объяснения широкого круга наблюдаемых явлений. При этом наблюдаемые явления описываются в рамках единого понятийного аппарата и не требуют специфических допущений для описания ...
... активность тиамина и некоторых его производных. За последние 20 лет наряду выяснением механизма основных реакций, в которых каталитическую роль играет ТДФ, стали накапливаться данные о высокой биологической активности других некоферментных производных тиамина. Отчетливо наметились два направления исследований: возможное, участие различных фосфорных эфиров витамина в активном переносе ...
... формами географической (территориально-механической) изоляции, известны и разные формы биологической изоляции, которые могут быть разбиты на три основные группы: эколого-этологическую, морфо-физиологическую и собственно генетическую. Биологическая изоляция приводит к уменьшению вероятности встречи особей разных полов в период размножения, снижению полового влечения и эффективности спаривания, к ...
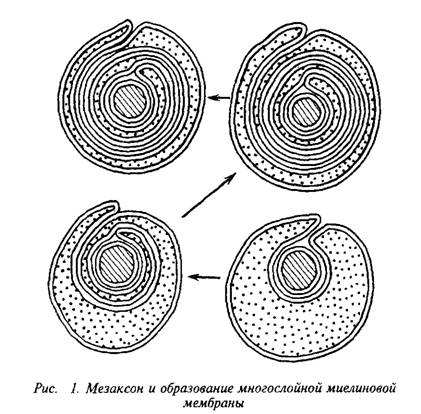
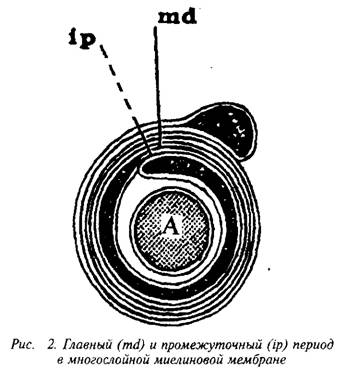
... и инозитолтрифосфат подвергаются химическим превращениям, требующим АТФ и ЦТФ и приводящим к восстановлению три-фосфоинозитида. Таким образом, цикл замыкается и уровень полифосфоинозитидов в мембране восстанавливается. 7. МИЕЛИН В ЦЕНТРАЛЬНОЙ НЕРВНОЙ СИСТЕМЕ Мозг человека содержит 120 г миелина, что составляет одну треть его сухой массы. Миелин – уникальное образование, организация которого ...
0 комментариев