Навигация
Савельев И.В. Курс общей физики. М.: Наука, 1977. Т. 1. § 36 – 39
1. Савельев И.В. Курс общей физики. М.: Наука, 1977. Т. 1. § 36 – 39.
2. Сивухин Д.В. Общий курс физики. М.: Наука, 1974. Т. 1. § 52, 55 – 59.
Лабораторная работа №7
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ПРИ ПОМОЩИ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: ознакомление с динамическим методом определения модуля сдвига.
Принадлежности: проволока из исследуемого материала, грузы, секундомер.
Если механический стержень с двумя симметрично расположенными грузами, подвешенный горизонтально к металлической проволоке, заставить колебаться, то уравнение движения для этого случая запишется в виде
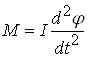 , (1)
, (1)
Здесь: М – момент сил, происходящий из упругих деформаций; I – момент инерции стержня с грузом; j – угол поворота стержня. Если амплитуда колебаний невелика, то для определения момента сил можно воспользоваться законом Гука в форме
M=fj, (2)
где f – модуль кручения проволоки (![]() ).
).
Момент М в этом случае вызван деформацией проволоки и стремится уменьшить, а не увеличить угол j. В формуле (2) поэтому необходимо изменить знак.
После подстановки (2) в (1) формула приобретает вид
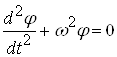 , (3)
, (3)
где ![]() .
.
Выражение (3) является дифференциальным уравнением 2-го порядка. Его решение находится в виде гармонической функции.
j=j0 sin(wt+q), (4)
где амплитуда j0 и фаза q определяются начальными условиями. Таким образом, w является угловой частотой крутильных колебаний стержня, период которых равен
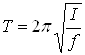 , (5)
, (5)
Следует заметить, что последняя формула получена для незатухающих колебании, в то время как на самом деле колебания стержня всегда затухают. Если, однако, затухание невелико, т. е. изменение амплитуды колебаний за период много меньше самой амплитуды, то формулой (5) можно пользоваться. Критерием ее применимости служит неравенство
n>>1, (6)
где n – число полных колебаний, после которого амплитуда уменьшается в 2 – 5 раз.
Отметим, что период Т, как видно из формулы (5), не зависит от амплитуды. Однако при больших амплитудах закон Гука нарушается и такая зависимость может проявляться. Таким образом, вторым условием применимости данного метода является соблюдение равенства Т = const.
Описание экспериментальной установки
Данные прибора: 2m = 410,8 + 410,8 = 821,6 г; расстояние от центров грузов до оси системы (при установке грузов внутренней стороной на риску):
1-я риска – 0,1 м, 2-я риска – 0,15 м, 3-я риска – 0,2 м, 4-я риска – 0,25 м, 5-я риска – 0,288 м.
Экспериментальная установка (рис. 7) состоит из длинной вертикально висящей проволоки 1, к нижнему концу которой прикреплен горизонтальный металлический стержень 2 с двумя симметрично расположенными грузами 3. Их положение на стержне можно фиксировать. Верхний конец проволоки зажат в цангу 4 и при помощи специального приспособления вместе с цангой может поворачиваться вокруг вертикальной оси. Таким образом, в системе можно возбудить крутильные колебания.
Ход работы
1. Прежде всего установите диапазон амплитуд, в котором выполняется условие (6). Для этого укрепите грузы на некотором расстоянии от проволоки и возбудите в системе крутильные колебания. Измеряя время нескольких полных колебаний, найдите период T1. Затем, уменьшив амплитуду вдвое, тем же способом найдите соответствующий период Т2. Если T1=T2 то для проведения измерений можно выбрать любую амплитуду, но не больше первой. Если же окажется, что T1 ¹ T2, то амплитуду необходимо уменьшить до такого значения j, начиная с которого для всех j0=j будет справедливо равенство T1 =T2.
2. Установите грузы так, чтобы их центры находились на некотором расстоянии L1 от оси системы, измерьте период, как описано выше. Если I – момент инерции стержня без грузов, а I1 – момент инерции грузов, то очевидно, что
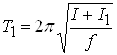 . (8)
. (8)
Изменив расстояние грузов до значения L2, аналогично получим
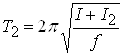 .(9)
.(9)
Из (8) и (9) следует
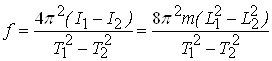 , (10)
, (10)
где m – масса одного груза.
Измерьте период колебаний для трех разных положений грузов на оси маятника (L1, L2, L3). Определите величину f по формуле (10) для нескольких (не менее трех) пар значений L1 и L2. Результаты измерений и вычислений занесите в таблицу:
Расстояние до груза | i | ti, c |
| (Dt1)2, c2 | T, c |
| L1=15 см | 1:5 | ||||
| L2=20 см | 1:5 | ||||
| L3=25 см | 1:5 |
3. Зная f, вычислите значение модуля сдвига G, который связан с модулем кручения формулой ![]() , где r – радиус проволоки (r=(1±0,01) мм), l – длина проволоки (l=(508±1) мм). Сравните экспериментальное значение модуля сдвига G с табличным значением для стали.
, где r – радиус проволоки (r=(1±0,01) мм), l – длина проволоки (l=(508±1) мм). Сравните экспериментальное значение модуля сдвига G с табличным значением для стали.
4. Вычислите погрешность результатов косвенного измерения f и G. Число колебаний N = 20; t – время, за которое происходит 20 колебаний; период одного колебания Т = t /N.
Контрольные вопросы
1.Как формулируется основной закон динамики вращательного движения?
2.В каком случае правую часть уравнения (1) можно записать в таком виде?
3.Что такое деформация кручения? Проиллюстрируйте графически деформацию кручения балки, закрепленной на одном из концов.
4.Каков физический смысл параметров f и G?
5.В каком случае справедлива формула М =fj?
6. Запишите уравнение гармонических незатухающих колебаний в дифференциальной форме и сравните его с уравнением (3). Какой вывод можно сделать из этого сравнения?
Когда гармонические колебания станут ангармоническими?
Рекомендуемая литература
Похожие работы
... о невероятных ухищрениях человеческого ума. Первый до сих пор известный достоверный документ об "осуществлении" идеи вечного двигателя относится к XIII веку. Еще до установления закона сохранения энергии в 1775 году было сделано заявление французской Академии, в котором говорилось о невозможности создания вечного двигателя. Вследствие чего Академия отказывалась принимать впредь подобные проекты ...
... а я не вижу оснований считать сохранение заряда более фундаментальным, чем сохранение анергии и импульса". В 1931 г. на физической конференции в Пасадене Паули доложил ученым о своей интерпретации ?-распада: "Законы сохранения выполняются, так как испускание ?-частиц сопровождается проникающей радиацией из нейтральных частиц... Сумма энергий ?-частицы и нейтральной частицы..., испущенных ядром в ...
... оно было бы совершенно бесполезно по отношению к другим объектам, предлагаемым обычно творцами вечного движения..» Здесь (правда, применительно только к механическому движению) закон сохранения «силы» и вытекающая из него невозможность вечного двигателя первого рода выражены совершенно четко. И далее: «...Такой способ исследования, несомненно, дорого обходится; он уже разрушил много семей. Часты ...
... , имеющие электрический заряд Q = -1 и Q = 1 соответственно. Также являются стабильными частицами нейтрино и антинейтрино, т.к. это самые легкие носители лептонных зарядов Le, , . 3. СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЕЙ СИСТЕМЫ Одним из важных открытий современного естествознания является тот факт, что все многообразие окружающего нас физического мира связано с тем или иным ...
0 комментариев