Навигация
Савельев И.В. Курс общей физики. М.: Наука, 1977. Т. 1. § 33, 38, 45, 64, 86
1. Савельев И.В. Курс общей физики. М.: Наука, 1977. Т. 1. § 33, 38, 45, 64, 86.
Лабораторная работа №8
ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ В ПОЛЕ ТЯЖЕСТИ НА МАШИНЕ АТВУДА
Цель работы: опытное изучение равноускоренного движения и нахождение ускорения свободного падения.
Принадлежности: машина Атвуда, секундомер, набор перегрузков.
Краткая теория
Машина Атвуда предназначена для исследования закона движения тел в поле земного тяготения. Естественнее всего изучать этот закон, исследуя свободное падение тел, но этому, однако, мешает большая величина ускорения свободного падения. Поэтому опыт возможен либо при очень большой высоте прибора (намного выше высоты комнаты), либо с применением специальных методов, позволяющих точно измерить небольшие промежутки времени (доли секунды). Машина Атвуда позволяет избежать этих трудностей и замедлить движение до удобных скоростей.
Машина Атвуда состоит из вертикальной штанги 2 со шкалой (рис. 8), сверху которой установлен легкий пластмассовый блок, укрепленный на корундовых подшипниках и способный вращаться вокруг оси с незначительным трением. Через блок перекинута нить, на концах которой прикреплены грузы А и В, имеющие равные массы М. На груз А могут надеваться один, два или несколько перегрузков. Система грузов в этом случае выходит из равновесия и начинает двигаться ускоренно.
Найдем закон движения груза А. При расчетах будем пользоваться неподвижной системой координат, центр которой совпадает с осью блока. Ось ОХ направлена вниз. На груз А действуют две силы – сила тяжести (M+m)g и сила натяжения левой части нити T1, m – масса перегрузка, лежащего на грузе А. По второму закону Ньютона:
(М + m)g –T1 = (М+m)a, (1)
где a – ускорение груза А.
1– подставка (столик), передвигающаяся по штанге,
2– вертикальная штанга со шкалой,
3– грузы одинаковых масс,
4– электромагнит для удерживания грузов,
5– легкий пластмассовый блок,
6– тонкая капроновая нить.
Применим второй закон Ньютона к движению груза 3. В силу нерастяжимости нити ускорение груза 3 равно ускорению груза А по абсолютной величине и направлено в противоположную сторону, следовательно, оно равно а. Натяжение правого конца нити обозначим через Т2. Тогда
Mg-T2=Ma. (2)
Запишем основное уравнение динамики вращательного движения твердых тел применительно к блоку:
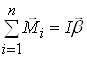 .
.
Здесь ![]() – суммарный момент сил относительно оси вращения, приложенный к блоку; I – момент инерции вращающего тела;
– суммарный момент сил относительно оси вращения, приложенный к блоку; I – момент инерции вращающего тела; ![]() – угловое ускорение.
– угловое ускорение.
Угловое ускорение связано с линейным ускорением a следующим образом
![]() ,
,
где R – радиус блока.
Запишем для пластмассового блока (с учетом двух последних выражений) основной закон динамики вращательного движения:
![]() , (3)
, (3)
где I – момент инерции блока; R – радиус блока (R=0,066±0,001 м). Очевидно, что если подобран перегрузок m0, при котором система движется равномерно, то момент силы трения
МTP = m0 gR.
Учитывая, что  , где М0 – масса блока, уравнение (3) перепишется в виде
, где М0 – масса блока, уравнение (3) перепишется в виде
![]() . (4)
. (4)
Из системы уравнений (1), (2), (4) найдем линейное ускорение:
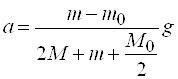 . (5)
. (5)
Здесь M0 – масса блока (M0 =(0,115± 0,0005) кг); М =(0,161±0,0005) кг – масса груза А и В; m0 = 0,2 г (определяется экспериментально).
Таким образом, движение груза А происходит равноускоренно и подчиняется уравнению (5). Формула (5) может служить для определения ускорения g. Эксперимент осложняется, однако, тем обстоятельством, что не существует простых способов прямого измерения ускорения a. Для определения a воспользуемся равноускоренным характером движения и будем измерять путь S и время t движения груза. Эти величины связаны известным соотношением:
 . (6)
. (6)
Из (6) выразим ускорение а:
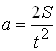 . (7)
. (7)
Экспериментальная часть
Эксперимент выполняется в следующем порядке. Один из имеющихся перегрузков кладут на груз А. Груз А поднимают на определённую высоту и фиксируют, подав ток в катушку электромагнита. Секундомер ставится на нуль. По шкале отмечается высота поднятия груза S над столиком.
Теперь следует разорвать цепь электромагнита и одновременно включить секундомер. При соприкосновении груза А со столиком секундомер выключают и замечают время опускания груза А. Зная S и t, нетрудно посчитать a по формуле (7), Опыт повторяют 5 раз и записывают полученные данные в таблицу:
№ | Масса перегрузки | ||||||||||||||
| M=2 г | M=4 г | M=6 г | |||||||||||||
| i | S1 м | ti c | t c | Dti2 c2 | a1 м/с2 | S1 м | ti c | t c | Dti2 c2 | a2 м/с2 | S1 м | ti c | t c | Dti2 c2 | a3 м/с2 |
| S2 м | ti c | t c | Dti2 c2 | a1 м/с2 | S2 м | ti c | t c | Dti2 c2 | a2 м/с2 | S2 м | ti c | t c | Dti2 c2 | a3 м/с2 | |
| 1 : 5 | |||||||||||||||
| S3 м | ti c | t c | Dti2 c2 | a1 м/с2 | S3 м | ti c | t c | Dti2 c2 | a2 м/с2 | S3 м | ti c | t c | Dti2 c2 | a3 м/с2 | |
| 1 : 5 | |||||||||||||||
![]()
Прежде чем приступить к систематическим измерениям, полезно проделать несколько опытов при разных S и t для того, чтобы убедиться в правильности работы установки. Вычисленное по экспериментальным данным по формуле (5) значение g следует сопоставить с табличным.
Экспериментально определить m0. Для этого используют миллиграммовые перегрузки разновеса; их кладут на груз А; постепенно увеличивая нагрузку до тех пор, пока груз А не начнет опускаться.
Ход работы
1.На груз А положить перегрузок и измерить время прохождения расстояния S не менее пяти раз.
2.Повторить опыт для различных перегрузков: 2 г, 4 г, 6 г.
3.Повторить опыт для трех различных высот подъёма груза.
4.Полученные данные изобразить графически t=F(S1/2). Проверить равноускоренный характер движения.
5.Вычислить значения всех ускорений a. Найти среднее значение и погрешности в определении a для каждого перегрузка.
6.Используя найденные значения a, вычислить значения g и сравнить их с табличными. Оценить точность найденного значения по формулам:
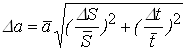 ,
,
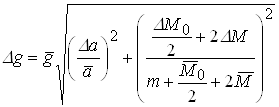 .
.
Контрольные вопросы
1.Сформулируйте и запишите второй закон Ньютона в дифференциальной форме.
2.Дайте определение момента сил, момента инерции, линейного и углового ускорения. Выведите связь линейного и углового ускорения.
3.Изменится ли натяжение нити (при движении грузов), если один перегрузок заменить другим?
4.Как изменится ускорение системы, если увеличить массу постоянных грузов А и В (не меняя массы перегрузка и сил трения)?
5.Почему система движется, хотя сила трения больше веса перегрузка?
6.Почему не рекомендуется ставить платформу слишком близко к началу шкалы?
7.Почему найденное значение g отличается от табличного?
Рекомендуемая литература
1.Савельев И.В. Курс общей физики. Т. 1: Механика, колебания и волны, молекулярная физика. М.: Наука, 1973. § 14, 16, 19, 21.
2.Иверонова В.И. Физический практикум. 1967. С. 51.
Похожие работы
... о невероятных ухищрениях человеческого ума. Первый до сих пор известный достоверный документ об "осуществлении" идеи вечного двигателя относится к XIII веку. Еще до установления закона сохранения энергии в 1775 году было сделано заявление французской Академии, в котором говорилось о невозможности создания вечного двигателя. Вследствие чего Академия отказывалась принимать впредь подобные проекты ...
... а я не вижу оснований считать сохранение заряда более фундаментальным, чем сохранение анергии и импульса". В 1931 г. на физической конференции в Пасадене Паули доложил ученым о своей интерпретации ?-распада: "Законы сохранения выполняются, так как испускание ?-частиц сопровождается проникающей радиацией из нейтральных частиц... Сумма энергий ?-частицы и нейтральной частицы..., испущенных ядром в ...
... оно было бы совершенно бесполезно по отношению к другим объектам, предлагаемым обычно творцами вечного движения..» Здесь (правда, применительно только к механическому движению) закон сохранения «силы» и вытекающая из него невозможность вечного двигателя первого рода выражены совершенно четко. И далее: «...Такой способ исследования, несомненно, дорого обходится; он уже разрушил много семей. Часты ...
... , имеющие электрический заряд Q = -1 и Q = 1 соответственно. Также являются стабильными частицами нейтрино и антинейтрино, т.к. это самые легкие носители лептонных зарядов Le, , . 3. СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЕЙ СИСТЕМЫ Одним из важных открытий современного естествознания является тот факт, что все многообразие окружающего нас физического мира связано с тем или иным ...
0 комментариев