Навигация
Если соленоидальное поле задано в односвязной области, то поток вектора через любую замкнутую поверхность этой области равно нулю
1. Если соленоидальное поле задано в односвязной области, то поток вектора через любую замкнутую поверхность этой области равно нулю.
Пусть ![]() - соленоидальное поле в односвязной области. Тогда поток вектора
- соленоидальное поле в односвязной области. Тогда поток вектора ![]() через любую поверхность
через любую поверхность ![]() натянутую на заданный контур Г, не зависит от вида этой поверхности, а зависит лишь от контура.
натянутую на заданный контур Г, не зависит от вида этой поверхности, а зависит лишь от контура.
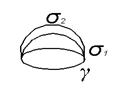
![]() применим теорему Остроградского-Гаусса.
применим теорему Остроградского-Гаусса.
![]()
![]()
![]()
2. Свойства векторной трубки.
Определение. Векторной линией называется линия в каждой точке которой направление касательной к ней совпадает с направлением поля ![]() .
.
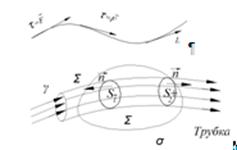
![]() векторной линии
векторной линии ![]() .
.
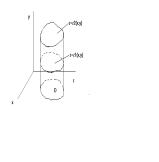
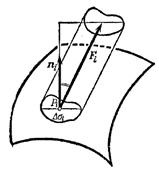
Возьмем в поле ![]() замкнутый контур
замкнутый контур ![]() и проведем через его точки векторные линии
и проведем через его точки векторные линии
Любая другая векторная линия проходящая через точки контура ![]() проходит либо внутри трубки либо вне трубки.
проходит либо внутри трубки либо вне трубки.
В случае потока жидкости , векторная трубка -это часть пространства, которую заполняет при своем перемещении объем жидкости.
Интенсивностью векторной трубки называется поток поля через поперечное сечение этой трубки.
3. Если поле соленоидальное в односвязной области ![]() , то интенсивность векторной трубки постоянна вдоль всей трубки.
, то интенсивность векторной трубки постоянна вдоль всей трубки.
Доказательство:
![]()
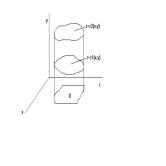
![]() - боковая поверхность, векторные линии перпендикулярны
- боковая поверхность, векторные линии перпендикулярны ![]() . Следовательно
. Следовательно ![]() (нормаль к
(нормаль к ![]() есть нормаль поля
есть нормаль поля ![]() т.е.
т.е. ![]() )
) ![]()
![]() и
и ![]() имеют противоположные направления.
имеют противоположные направления.
![]() .
.
Поток ![]() через любое поперечное одно и тоже если
через любое поперечное одно и тоже если ![]() соленоидальное.
соленоидальное.
4. В соленоидальном поле ![]() векторные линии не могут ни начинаться ни заканчиваться внутри поля. Они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви.
векторные линии не могут ни начинаться ни заканчиваться внутри поля. Они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви.
Доказательство:
По свойству 3 интенсивность трубки одинакова , хотя поперечное сечение в точке М равно нулю, в т М ![]() . Это невозможно т.к.
. Это невозможно т.к. ![]() непрерывен в любой точке.
непрерывен в любой точке.
![]()
![]()
Теорема Стокса.
Вихрь. Ротор.
Циркуляция.
1. Теорема Стокса
![]() .
.
С понятием циркуляции тесно связано понятие ротора или вихря. Локальной характеристикой поля ![]() связанной с завихренностью является ротор.
связанной с завихренностью является ротор.
Плоское поле.
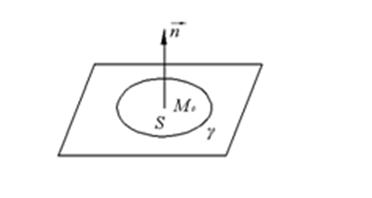
S площадь внутри ![]()
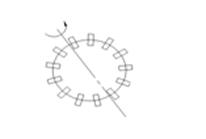
![]() поле скоростей текущей жидкости
поле скоростей текущей жидкости ![]()
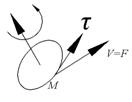
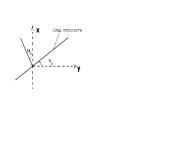
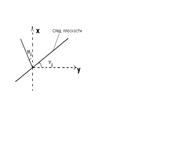
В поле ![]() поместим колесо с лопастями, вдоль
поместим колесо с лопастями, вдоль ![]() . Частицы жидкости, действуя на эти лопасти создадут вращательный момент, суммарное действие которых приведут колесо во вращение вокруг своей оси. Вращательное действие поля скоростей жидкости
. Частицы жидкости, действуя на эти лопасти создадут вращательный момент, суммарное действие которых приведут колесо во вращение вокруг своей оси. Вращательное действие поля скоростей жидкости ![]() будет в любой точке М характеризовать
будет в любой точке М характеризовать ![]() на касательной
на касательной ![]() к окружности
к окружности ![]() , т.е. скалярное произведение
, т.е. скалярное произведение ![]() . Суммирование
. Суммирование ![]() вращательных действии жидкости по всему контуру колесика приведут к понятию циркуляции вектора
вращательных действии жидкости по всему контуру колесика приведут к понятию циркуляции вектора ![]() =
=![]()
Будет определять угловую скорость вращения колеса, а знак циркуляции покажет в какую сторону вращается колесико относительно выбранного направления.
Циркуляция любого поля ![]() определяет его вращательную способность вокруг данного направления и характеризует завихренность поля
определяет его вращательную способность вокруг данного направления и характеризует завихренность поля ![]() в этом направлении.
в этом направлении.
Чем меньше ![]() тем больше циркуляция, больше завихренность.
тем больше циркуляция, больше завихренность.
![]() . Максимум вихря, если
. Максимум вихря, если ![]()
![]()
![]()
![]()
![]() - плотность циркуляции
- плотность циркуляции ![]() в точке
в точке ![]() .
.
Если ![]() пространственное поле, то можно говорить о завихренности в направлении
пространственное поле, то можно говорить о завихренности в направлении ![]() .
.
![]()
![]()
![]() - завихренности в направлении
- завихренности в направлении ![]() .
.
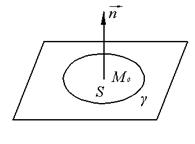
Определение: ![]() в точке
в точке ![]() называется вектор, проекция которого на каждое направление
называется вектор, проекция которого на каждое направление ![]() равна пределу отношения циркуляции векторного поля по контуру
равна пределу отношения циркуляции векторного поля по контуру ![]() в плоской области
в плоской области ![]() , перпендикулярной этому направлению
, перпендикулярной этому направлению ![]() , к величине площади S этой области, когда
, к величине площади S этой области, когда ![]() , а область
, а область ![]() стягивается в точке
стягивается в точке ![]() т. е.,
т. е.,
![]()
![]() - контур лежащий в плоскости перпендикулярной к вектору
- контур лежащий в плоскости перпендикулярной к вектору ![]()
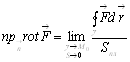
Теорема Стокса. ![]() -поверхностно-односвязная область.
-поверхностно-односвязная область. ![]() - кусочно- гладкий контур в
- кусочно- гладкий контур в ![]() ,
, ![]() -кусочно-гладкая поверхность натянутая на
-кусочно-гладкая поверхность натянутая на ![]() .
.
Следовательно циркуляция вектора ![]() вдоль
вдоль ![]() равна потоку
равна потоку ![]() - вихря
- вихря ![]() через
через ![]() в направлении
в направлении ![]()
Теорема 2.
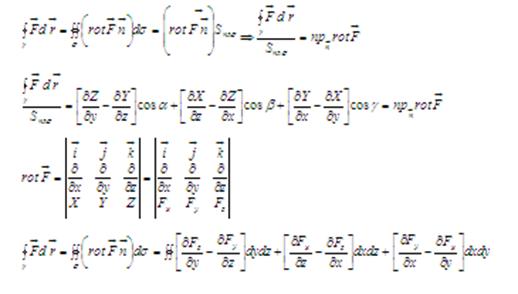
В частности
![]() .
.![]()
![]()
Пример. Найти циркуляцию ![]() по сечению сферы
по сечению сферы ![]() плоскостью
плоскостью ![]() .
.
Решение.
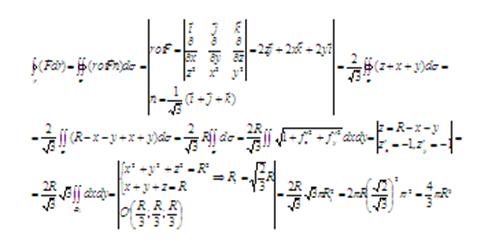
Потенциальное поле.
Свойства.
Потенциал поля.
Восстановление потенциала U(M) по ![]()
Потенциальное поле.
Определение. Векторное поле ![]() называется потенциальным в области
называется потенциальным в области ![]() , если существует скалярное поле
, если существует скалярное поле ![]() является полем градиента этого скалярного поля
является полем градиента этого скалярного поля ![]() .
.
 ;
;![]()
![]() .
.
Поле ![]() -называется потенциалом поля
-называется потенциалом поля ![]() .
.
Свойства: 1) Если ![]() потенциальное поле
потенциальное поле 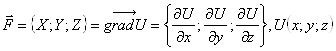 определяется однозначно с точностью до
определяется однозначно с точностью до ![]() .
.![]() .
.
2) Если ![]() -потенциальное , т.е.
-потенциальное , т.е. 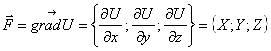
![]() не зависит от пути интегрирования, а только от начала и конца пути.
не зависит от пути интегрирования, а только от начала и конца пути.
3) Чтобы поле ![]() было потенциальным, необходимо чтобы
было потенциальным, необходимо чтобы ![]() был полным дифференциалом некоторой функции
был полным дифференциалом некоторой функции ![]()
![]()
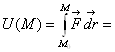
Если ![]() -потенциальное, то для вычисления криволинейного интеграла
-потенциальное, то для вычисления криволинейного интеграла ![]() достаточно найти разность
достаточно найти разность ![]()
4)![]() не зависит от пути интегрирования,
не зависит от пути интегрирования,
![]()
Для того чтобы поле было потенциальным, необходимо чтобы оно было безвихревым.
Нахождение потенциала ![]() векторного поля
векторного поля ![]()
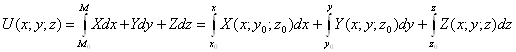
Пример. ![]()
1) потенциальное ли поле?
2) Найти ![]()
1) 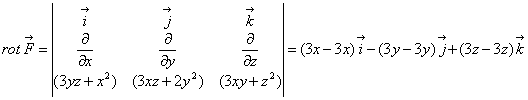
2) ![]()
![]()
![]()
Пример. Потенциал поля скоростей текущей жидкости ![]() . Вычислить количество жидкости, протекающей за единицу времени через отрезок прямой от О(0;0) до А(1;1).
. Вычислить количество жидкости, протекающей за единицу времени через отрезок прямой от О(0;0) до А(1;1).
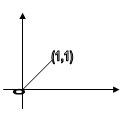
![]()
![]()
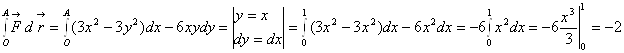
![]()
Поток
![]()
Доказательство:
![]() =
=![]() .
.
В потенциальном поле циркуляция по замкнутому контуру равна нулю.
1. Поток
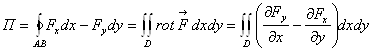 .
.
Для поля замкнутого поток равен нулю.
Пример. Вычислить поток и циркуляцию ![]() вдоль замкнутого контура
вдоль замкнутого контура ![]()
Поток
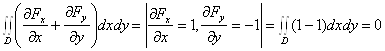
Циркуляция

II способ. Поток в плоском поле
![]()
Поток 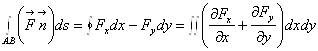
Циркуляция 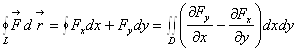
В плоском поле ![]()
![]()
Литература.
1. Ильин В.А. , Садовничий В.А., Сендов Б.Х. Математический анализ. 1-2 том. Изд. МГУ,1989г.
2. Виноградова И.А. , Олексич С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. Часть 1,2 Изд. МГУ. Серия классический университетский учебник 250 летию МГУ 2005г.
3. Шилов Г.Е. Математический анализ. Часть 1,2. Москва. Изд.Лань. 2002г.-880стр.
4. Лунгу К.Н. Сборник задач по математике. Часть 1,2. Москва. Айрис пресс 2005г.
Похожие работы
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
ормулу Грина для области Д: D P(x,y), Q(x,y) , Вычисление площадей через крив интеграл Применим ф. Грина, т.е. выразим его через криволинейный интеграл по границе области. 1. Q = x P = 0 2. Q = 0 P = -y Суммируем 1 и 2 : Пример: Вычислить площадь эллипса . Сделаем замену переменных 0 £ t £ 2p Вопрос №6 Неприрывную кривую назыв. простой кривой ( ...
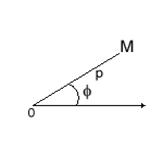
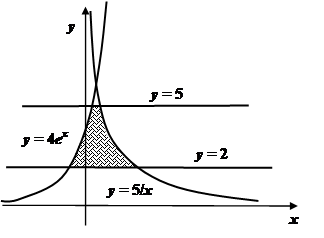
... так: , (10) где F1 и F2 – функции, полученные при подстановке в функцию f вместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты. 1.4 Геометрические и физические приложения кратных интегралов 1) Площадь плоской области S: (11) Пример 1. Найти площадь фигуры D, ограниченной линиями у = 2, у = 5. Решение. Эту площадь удобно вычислять, считая у ...
... с вершинами в точках А(0;0), В(0;1), С(½; 0). Найдем координаты единичной нормали к плоскости: Вычислим соответствующий поверхностный интеграл: Заключение В данной работе была рассмотрена дискретная теория поля. Вначале было введено понятие поверхностного интеграла. Поверхностный интеграл первого рода от функции f(M) = f(x, y, z) по поверхности S обозначается . ...
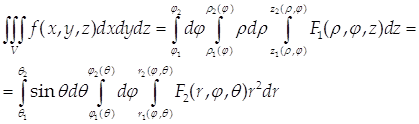
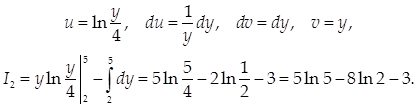

0 комментариев