Обобщённо булевы решетки

Федеральное агентство по образованию

Государственное образовательное учреждение
высшего профессионального образования
Вятский государственный гуманитарный университет

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Обобщенно булевы решетки

Выполнил:

студент V курса математического факультета

Онучин Андрей Владимирович

Научный руководитель:

к.ф.-м.н., доцент кафедры алгебры и геометрии ВятГГУ
Чермных Василий Владимирович

Рецензент:

д.ф.-м.н., профессор, зав. кафедрой алгебры и геометрии ВятГГУ

Вечтомов Евгений Михайлович

Работа допущена к защите в государственной аттестационной комиссии

«___» __________2005 г. Зав. кафедрой Е.М. Вечтомов

«___»__________2005 г. Декан факультета В.И. Варанкина

Киров

2005

Содержание

Введение.......................................................................................................... 3

Глава 1............................................................................................................. 4

1.1. Упорядоченные множества................................................................... 4

1.2. Решётки.................................................................................................. 5

1.3. Дистрибутивные решётки..................................................................... 7

1.4. Обобщённые булевы решётки, булевы решётки................................. 8

1.5. Идеалы................................................................................................... 9

Глава 2........................................................................................................... 11

2.1. Конгруэнции....................................................................................... 11

2.2. Основная теорема............................................................................... 16

Библиографический список.......................................................................... 22

Введение

 

Булева решётка представляет собой классический математический объект, который начал интенсивно изучаться в работах М. Стоуна 30-е годы 20-го века, расширением этого понятия до обобщённо булевых решёток занимались Г. Гретцер и Е. Шмидт в своих трудах конца 50-х годов.

Цель данной работы: установление взаимно однозначного соответствия между конгруэнциями и идеалами в обобщённо булевых решётках. (Для булевых решёток это положение доказано в книге [2], кроме того, сформулировано в книге [3] в качестве упражнений). А также – установление связи между обобщённо булевыми решётками и булевыми кольцами.

Данная дипломная работа состоит из двух глав: в первой главе даны основные понятия, а так же содержатся базовые сведения из теории решёток. Кроме того, в первой главе рассмотрено несколько простейших теорем.

Вторая глава представляет собой основную часть данной дипломной работы. Опираясь на работы Гретцера Г., но более подробно, рассмотрены свойства конгруэнций и связь конгруэнций и идеалов в обобщённо булевых решётках (Теоремы 2.1, 2.2, 2.3.). Кроме того реализована основная цель данной дипломной работы: установлена связь между булевыми кольцами и обобщённо булевыми решётками (Основная теорема).

Глава 1 1.1. Упорядоченные множества

 

Упорядоченным множеством P называется непустое множество, на котором определено бинарное отношение , удовлетворяющее для всех  следующим условиям:

1. Рефлексивность: .

2. Антисимметричность. Если  и , то .

3. Транзитивность. Если  и , то .

Если  и , то говорят, что  меньше или  больше , и пишут  или .

Примеры упорядоченных множеств:

1.  Множество целых положительных чисел, а  означает, что  делит .

2.  Множество всех действительных функций  на отрезке  и  означает, что  для .

Цепью называется упорядоченное множество, на котором для любых  имеет место  или .

Используя отношение порядка, можно получить графическое представление любого конечного упорядоченного множества P. Изобразим каждый элемент множества P в виде небольшого кружка, располагая x выше y, если . Соединим x и y отрезком. Полученная фигура называется диаграммой упорядоченного множества P.

Примеры диаграмм упорядоченного множества:   1.2. Решётки

 

Верхней гранью подмножества Х в упорядоченном множестве Р называется элемент a из Р, больший или равный всех x из X.

Точная верхняя грань подмножества X упорядоченного множества P – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом sup X и читается «супремум X».

Согласно аксиоме антисимметричности упорядоченного множества, если точная верхняя грань существует, то она единственна.

Понятия нижней грани и точной нижней грани (которая обозначается inf X и читается «инфинум») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань X существует, то она единственна.

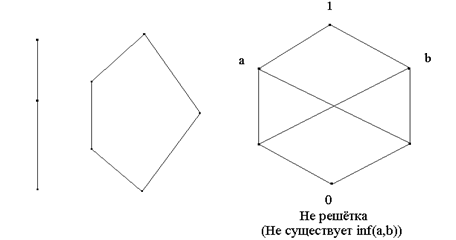Решёткой  называется упорядоченное множество L, в котором любые два элемента x и y имеют точную нижнюю грань, обозначаемую , и точную верхнюю грань, обозначаемую .

Примеры решёток:

Примечание. Любая цепь является решёткой, т.к.  совпадает с меньшим, а  с большим из элементов .

Наибольший элемент, то есть элемент, больший или равный каждого элемента упорядоченного множества, обозначают 1, а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают 0.

На решётке можно рассматривать две бинарные операции:

 - сложение и

 - произведение

Эти операции обладают следующими свойствами:

1. ,  идемпотентность;

2. ,  коммутативность;

3. ,  ассоциативность;

4. ,  законы поглощения.

ТЕОРЕМА 1.1. Пусть L - множество с двумя бинарными операциями , обладающими свойствами (1) – (4). Тогда отношение  (или ) является порядком на L, а возникающее упорядоченное множество оказывается решёткой, причём:  и  .

Доказательство. Рефлексивность отношения  вытекает из свойства (1). Заметим, что оно является следствием свойства (4):

Если  и , то есть  и , то в силу свойства (2), получим . Это означает, что отношение  антисимметрично.

Если  и , то применяя свойство (3), получим: , что доказывает транзитивность отношения .

Применяя свойства (3), (1), (2), получим:

,

.

Следовательно,  и .

Если  и , то используя свойства (1) – (3), имеем:

, т.е. .

По определению точней верхней грани убедимся, что .

Из свойств (2), (4) вытекает, что  и .

Если  и , то по свойствам (3), (4) получим:

.

Отсюда по свойствам (2) и (4) следует, что

.

Таким образом, .

Пусть L решётка, тогда её наибольший элемент 1 характеризуется одним из свойств:

1. .

2. .

Аналогично характеризуется наименьший элемент :

1. 

2. .

 

1.3. Дистрибутивные решётки

 

Решётка L называется дистрибутивной, если для любых  выполняется:

D1. .

D2. .

В любой решётке тождества D1 и D2 равносильны. Доказательство этого факта содержится в книге [2], стр. 24.

Примеры дистрибутивных решёток:

1.  Множество целых положительных чисел,  означает, что  делит . Это решётка с операциями НОД и НОК.