Любая цепь является дистрибутивной решёткой

Любая цепь является дистрибутивной решёткой Закон дистрибутивности

21130

знаков

таблиц

изображений

Обобщённо булевы решетки Читать далее: Закон дистрибутивности

2. Любая цепь является дистрибутивной решёткой.

ТЕОРЕМА 1.2. Решётка L с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида

Доказательство этой теоремы можно найти в книге [1].

1.4. Обобщённо булевы решётки, булевы решётки

Всюду далее под словом «решётка» понимается произвольная дистрибутивная решётка с 0.

Решётка L называется обобщённой булевой, если для любых элементов и d из L, таких что существует относительное дополнение на интервале , т.е. такой элемент из L, что и .

(Для , , интервал |; для , можно так же определить полуоткрытый интервал |).

ТЕОРЕМА 1.3. (О единственности относительного дополнения в обобщённо булевой решётке). Каждый элемент обобщённо булевой решётки L имеет только одно относительное дополнение на промежутке.

Доказательство. Пусть для элемента существует два относительных дополнения и на интервале . Покажем, что . Так как относительное дополнение элемента на промежутке , то и , так же относительное дополнение элемента на промежутке , то и .

Отсюда

таким образом , т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.

Решётка L называется булевой, если для любого элемента из L существует дополнение, т.е. такой элемент из L, что и

ТЕОРЕМА 1.4. (О единственности дополнения в булевой решётке). Каждый элемент булевой решётки L имеет только одно дополнение.

Доказательство аналогично доказательству теоремы 1.3.

ТЕОРЕМА 1.5. (О связи обобщённо булевых и булевых решёток).

Любая булева решётка является обобщённо булевой, обратное утверждение не верно.

Доказательство. Действительно, рассмотрим произвольную булеву решётку L. Возьмём элементы a и d из L, такие что . Заметим, что относительным дополнением элемента a до элемента d является элемент , где a’ – дополнение элемента a в булевой решётке L. Действительно, , кроме того . Отсюда следует, что решётка L является обобщённо булевой.

1.5. Идеалы

Подрешётка I решётки L называется идеалом, если для любых элементов и элемент лежит в I. Идеал I называется собственным, если . Собственный идеал решётки L называется простым, если из того, что и следует или .

Так как непустое пересечение любого числа идеалов снова будет идеалом, то мы можем определить идеал, порождённый множеством H в решётке L, предполагая, что H не совпадает с пустым множеством. Идеал, порождённый множеством H будет обозначаться через (H]. Если , то вместо будем писать и называть главным идеалом.

ТЕОРЕМА 1.5. Пусть L – решётка, а H и I – непустые подмножества в L, тогда I является идеалом тогда и только тогда, когда если , то , и если , то .

Доказательство. Пусть I – идеал, тогда влечёт за собой , так как I – подрешётка. Если , то и условия теоремы проверены.

Обратно, пусть I удовлетворяет этим условиям и . Тогда и так как , то , следовательно, I – подрешётка. Наконец, если и , то , значит, и I является идеалом.

Глава 2 2.1. Конгруэнции

Отношение эквивалентности (т.е. рефлексивное, симметричное и транзитивное бинарное отношение) на решётке L называется конгруэнцией на L, если и совместно влекут за собой и (свойство стабильности). Простейшими примерами являются ω, ι, определённые так:

(ω); (ι) для всех .

Для обозначим через смежный класс, содержащий элемент , т.е. ‌|

Пусть L – произвольная решётка и . Наименьшую конгруэнцию, такую, что для всех , обозначим через и назовём конгруэнцией, порождённой множеством .

ЛЕММА 2.1. Конгруэнция существует для любого .

Доказательство. Действительно, пусть Ф = | для всех . Так как пересечение в решётке совпадает с теоретико-множественным пересечением, то для всех . Следовательно, Ф=.

В двух случаях мы будем использовать специальные обозначения: если или и - идеал, то вместо мы пишем или соответственно. Конгруэнция вида называется главной; её значение объясняется следующей леммой:

ЛЕММА 2.2. =|.

Доказательство. Пусть , тогда , отсюда . С другой стороны рассмотрим , но тогда . Поэтому и .

Заметим, что - наименьшая конгруэнция, относительно которой , тогда как - наименьшая конгруэнция, такая, чтосодержится в одном смежном классе. Для произвольных решёток о конгруэнции почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции :

ТЕОРЕМА 2.1. Пусть - дистрибутивная решётка, и . Тогда и .

Доказательство. Обозначим через Ф бинарное отношение, определённое следующим образом: и .

Покажем, что Ф – отношение эквивалентности:

1) Ф – отношение рефлексивности: x·a = x·a ; x+b = x+b;

2) Ф – отношение симметричности:

x·a = y·a и x+b = y+b y·a = x·a и y+b = x+b ;

3) Ф – отношение транзитивности.

Пусть x·a = y·a и x+b = y+b и пусть y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом .

Из всего выше обозначенного следует, что Ф – отношение эквивалентности.

Покажем, что Ф сохраняет операции. Если и zL, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно, . Аналогично доказывается, что и, таким образом, Ф – конгруэнция.

Наконец, пусть - произвольная конгруэнция, такая, что , и пусть . Тогда x·a = y·a, x+b = y+b , и . Поэтому вычисляя по модулю , получим

, т.е. , и таким образом, .

СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 2.1. Пусть I – произвольный идеал дистрибутивной решётки L. Тогда в том и только том случае, когда для некоторого . В частности, идеал I является смежным классом по модулю .

Доказательство. Если , то и элементы x·y·i, i принадлежат идеалу I.

Действительно .

Покажем, что .

Воспользуемся тем, что (*), заметим, что и , поэтому мы можем прибавить к тождеству (*) или , и тождество при этом будет выполняться.

Прибавим : , получим .

Отсюда . Таким образом,.

Обратно согласно лемме 2, ‌‌‌‌‍|

Однако и поэтому ‌‌‌‌‍|

Если , то откуда

Действительно, (**).

Рассмотрим правую часть этого тождества:

Объединим первое и второе слагаемые –

Объединим первое и третье слагаемые –

таким образом (***)

Заметим, что , поэтому прибавим к обеим частям выражения (***) y:

Но , отсюда .

Следовательно, условие следствия из теоремы 2.1. выполнено для элемента . Наконец, если и , то , откуда и , т.е. является смежным классом.

ТЕОРЕМА 2.2. Пусть L – булева решётка. Тогда отображение является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L. (Под понимаем класс нуля по конгруэнции , под понимаем решётку конгруэнций.)

Доказательство. В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс определяет конгруэнцию . Это утверждение, однако, очевидно. Действительно тогда и только тогда, когда (*), последнее сравнение в свою очередь равносильно сравнению , где с – относительное дополнение элемента в интервале .

Действительно, помножим выражение (*) на с:

, но, а , отсюда .

Таким образом, в том и только том случае, когда .

Примечание. Приведённое доказательство не полностью использует условие, что L – дистрибутивная решётка с дополнениями. Фактически, мы пользовались только тем, что L имеет нуль и является решёткой с относительными дополнениями. Такая решётка называется обобщённой булевой решёткой.

ТЕОРЕМА 2.3 (Хасимото [1952]). Пусть L – произвольная решётка. Для того, чтобы существовало взаимно однозначное соответствие между идеалами и конгруэнциями решётки L, при котором идеал, соответствующий конгруэнции , являлся бы смежным классом по , необходимо и достаточно, чтобы решётка L была обобщённой булевой.

Доказательство. Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.

Идеалом, соответствующим конгруэнции , должен быть (0]; следовательно, L имеет нуль 0.

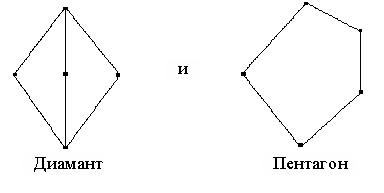
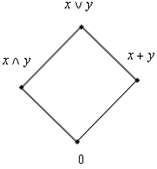
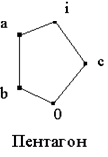Если L содержит диамант , то идеал (a] не может быть смежным классом, потому что из следует и . Но , значит, любой смежный класс, содержащий , содержит и , и .

Аналогично, если L содержит пентагон и смежный класс содержит идеал , то и , откуда . Следовательно, этот смежный класс должен содержать и .

Итак, решётка L не содержит подрешёток, изоморфных ни диаманту, ни пентагону. Поэтому, по теореме 1.2., она дистрибутивна.

Пусть и . Согласно следствию из теоремы 2.1., для конгруэнции идеал так же является смежным классом, следовательно, , откуда . Опять применяя следствие из теоремы 2.1. получим, для некоторого . Так как , то и . Следовательно, о полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции образом мы должны только доказать, ______________ и , т.е. элемент является относительным дополнением элемента в интервале .

2.2. Основная теорема

(1) Пусть - обобщённая булева решётка. Определим бинарные операции на B, полагая и обозначая через относительное дополнение элемента в интервале . Тогда - булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству (а следовательно и тождествам , ).