Навигация
6. Закон дистрибутивности.
Проверим, выполняются ли аксиомы кольца:
1. Относительным дополнением до ![]() элемента
элемента ![]() будет элемент
будет элемент ![]() , а относительным дополнением
, а относительным дополнением ![]() элемент
элемент ![]()
![]() . В силу того, что
. В силу того, что ![]() , а так же единственности дополнения имеем
, а так же единственности дополнения имеем ![]() .
.
2. Покажем, что ![]() .
.
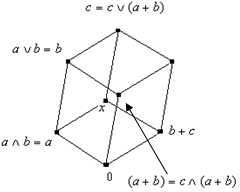 Рассмотрим все возможные группы вариантов:
Рассмотрим все возможные группы вариантов:
1) Пусть ![]() , тогда
, тогда ![]() (Далее везде под элементом x будем понимать сумму
(Далее везде под элементом x будем понимать сумму ![]() ).
).
Аналогично получаем ![]() в случаях
в случаях ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() . Заметим, что когда один из элементов равен нулю (например, c), то получаем тривиальные варианты (a+b=a+b).
. Заметим, что когда один из элементов равен нулю (например, c), то получаем тривиальные варианты (a+b=a+b).
2) Пусть ![]() , а элемент c не сравним с ними. Возможны следующие варианты:
, а элемент c не сравним с ними. Возможны следующие варианты:
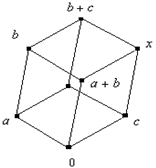
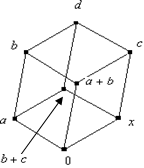
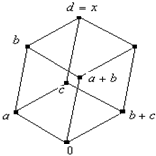
Нетрудно заметить, что во всех этих случаях ![]() , кроме того:
, кроме того:
если c=a+b, то (a+b)+c=0=a+(b+c);
если c=0, то получаем тривиальный вариант.
Вариант, когда c равен наибольшему элементу решётки d, мы уже рассматривали.
Если c=b, то (a+b)+c=(a+b)+b=a и a+(b+c)=a+(b+b)=a.
Если c=a, то (a+b)+c=(a+b)+a=b и a+(b+c)=a+(b+a)=b.
 Аналогично для случаев
Аналогично для случаев ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
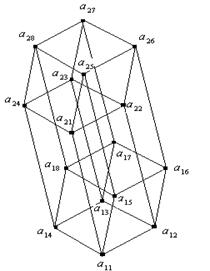
3) Под элементами нижнего уровня будем понимать элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. те элементы 4-х мерного куба, которые образуют нижний трёхмерный куб.
, т.е. те элементы 4-х мерного куба, которые образуют нижний трёхмерный куб.
Под элементами верхнего уровня будем понимать элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. те элементы 4-х мерного куба, которые образуют верхний трёхмерный куб.
, т.е. те элементы 4-х мерного куба, которые образуют верхний трёхмерный куб.
Под фразой «элемент верхнего уровня, полученный из элемента ![]() нижнего уровня сдвигом по соответствующему ребру» будем понимать элемент
нижнего уровня сдвигом по соответствующему ребру» будем понимать элемент ![]() верхнего уровня.
верхнего уровня.
Пусть a, b, c несравнимы. Рассмотрим следующие варианты: ![]() и
и ![]() .
.
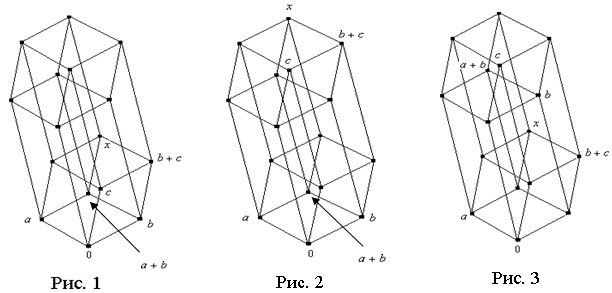 Пусть
Пусть ![]() . Заметим, что это возможно только в случаях, когда
. Заметим, что это возможно только в случаях, когда ![]() принадлежат нижнему уровню, причём лежат на позициях элементов
принадлежат нижнему уровню, причём лежат на позициях элементов ![]() (рис. 1). Либо a, b остаются на своих позициях, элемент c сдвигается на верхний уровень по соответствующему ребру (рис. 2). Либо элемент a остаётся на своей позиции, элементы b, c сдвигаются на верхний уровень по соответствующему ребру (рис 3).
(рис. 1). Либо a, b остаются на своих позициях, элемент c сдвигается на верхний уровень по соответствующему ребру (рис. 2). Либо элемент a остаётся на своей позиции, элементы b, c сдвигаются на верхний уровень по соответствующему ребру (рис 3).
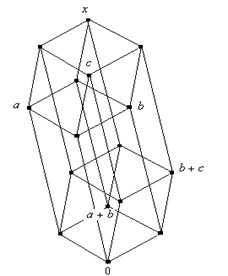 Нетрудно заметить, что во всех этих случаях
Нетрудно заметить, что во всех этих случаях ![]() .
.
Пусть ![]() , здесь так же
, здесь так же ![]() .
.
Таким образом мы рассмотрели все основные группы вариантов расположения элементов a, b, c и во всех этих случаях ассоциативность сложения выполняется.
3. Рассмотрим в решётке элемент ![]() , к нему существует относительное дополнение
, к нему существует относительное дополнение ![]() до элемента
до элемента ![]() , т.е.
, т.е. ![]() и
и ![]() . Учитывая, что в решётке
. Учитывая, что в решётке ![]() и
и ![]() , имеем следующее:
, имеем следующее: ![]() и
и ![]() . Отсюда
. Отсюда ![]() .
.
4. Рассмотрим относительное дополнение элемента ![]() до
до ![]() , это элемент
, это элемент ![]() . Таким образом:
. Таким образом: ![]() и
и ![]() . Учитывая, что в решётке выполняются тождества
. Учитывая, что в решётке выполняются тождества ![]() и
и ![]() имеем следующее:
имеем следующее: ![]() и
и ![]() . Отсюда
. Отсюда ![]() .
.
5. Так как в решётке выполняется ассоциативность ![]() , а так же имея
, а так же имея ![]() , то
, то ![]() .
.
6. Докажем дистрибутивность ![]() или что то же самое
или что то же самое
![]() (*).
(*).
Докажем, что дополнения левой и правой частей выражения (*) до верхней грани ![]() совпадают.
совпадают.
Нетрудно заметить, что дополнением правой части выражения (*) до элемента ![]() будет являться элемент
будет являться элемент ![]() .
.
Покажем это:
![]() , по определению относительного дополнения элемента
, по определению относительного дополнения элемента ![]() (
(![]() ), где за
), где за ![]() приняли элемент
приняли элемент ![]() , а элемент
, а элемент ![]() за
за ![]() .
.
![]() , по определению относительного дополнения элемента
, по определению относительного дополнения элемента ![]() (
(![]() ) , где за
) , где за ![]() приняли элемент
приняли элемент ![]() , а элемент
, а элемент ![]() за
за ![]() .
.
Покажем, что и для левой части (*) элемент ![]() будет являться относительным дополнением до верхней грани
будет являться относительным дополнением до верхней грани ![]() :
:
![]() , т.к.
, т.к. ![]() .
.
![]()
Мы показали, что дополнения элементов ![]() и
и ![]() до верхней грани
до верхней грани ![]() совпадают, следовательно, в силу единственности дополнения
совпадают, следовательно, в силу единственности дополнения ![]() . А значит и
. А значит и ![]() , т.е. дистрибутивность доказана.
, т.е. дистрибутивность доказана.
Таким образом, для ![]() все аксиомы кольца выполняются.
все аксиомы кольца выполняются.
Заметим, что ![]() выполняется в силу того, что
выполняется в силу того, что ![]() , а в решётке
, а в решётке ![]() .
.
Также выполняется ![]() , потому что
, потому что ![]() .
.
Таким образом, ![]() - булево кольцо.
- булево кольцо.
Доказательство (2). Частичную упорядоченность ![]() имеем исходя из того, что исходное булево кольцо
имеем исходя из того, что исходное булево кольцо ![]() - частично упорядоченное множество. Кроме того
- частично упорядоченное множество. Кроме того ![]() - решётка, т.к.
- решётка, т.к. ![]() существуют sup(x,y) и inf(x,y), заданные соответствующими правилами:
существуют sup(x,y) и inf(x,y), заданные соответствующими правилами: ![]() и
и ![]() .
.
Покажем, что решётка дистрибутивна, т.е. что выполняется тождество ![]() (*)
(*)
Рассмотрим левую часть выражения (*):
![]() .
.
Рассмотрим правую часть выражения (*):
![]() ,
,
т.о. тождество ![]() верно, т.е. решётка
верно, т.е. решётка ![]() является дистрибутивной.
является дистрибутивной.
Покажем, что у каждого элемента ![]() в дистрибутивной решётке
в дистрибутивной решётке ![]() есть относительное дополнение. Для этого рассмотрим произвольные элементы
есть относительное дополнение. Для этого рассмотрим произвольные элементы ![]() , но они так же должны являться элементами решётки
, но они так же должны являться элементами решётки ![]() , следовательно, в ней должны лежать и
, следовательно, в ней должны лежать и ![]() , которым в кольце соответствуют
, которым в кольце соответствуют ![]() .
.
Рассмотрим элемент булева кольца ![]() (в решётке лежит соответствующий ему элемент), заметим, что
(в решётке лежит соответствующий ему элемент), заметим, что
![]()
и ![]() .
.
Поэтому элемент ![]() будет являться в дистрибутивной решётке
будет являться в дистрибутивной решётке ![]() относительным дополнением
относительным дополнением ![]() до верхней грани
до верхней грани ![]() .
.
Таким образом, ![]() будет являться дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
будет являться дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
Библиографический список
1. Гретцер, Г. Общая теория решёток [Текст] / Г. Гретцер. – М.: Мир, 1982.
2. Биркгоф, Г. Теория решёток [Текст] / Г. Биркгоф. – М.: Наука, 1984.
3. Скорняков, Л.А. Элементы алгебры [Текст] / Л.А. Скорняков. – М.: Наука, 1989.
0 комментариев