Познавательный интерес младших школьников
Особенности исторического материала, изучаемого на уроках математики в начальной школе
Из истории задач с одинаковыми цифрами
Подготовка учителя к использованию познавательных заданий историко-математического характера
Анализ методической литературы
В новом задании нет нуля и одинаковых цифр
Навигация
Анализ методической литературы
Исторический материал, как одно из средств развития познавательной активности младших школьников на уроке математике
59835
знаков
6
таблиц
0
изображений
2.1.3 Анализ методической литературы
В папирусах Древнего Египта содержится большое число задач. В папирусе Райнда имеется задача на арифметическую прогрессию. «Тебе сказано: раздели 10 мер хлеба на 10 человек, если разность между
каждым человеком и следующим за ним составит 1/8 меры».
В клинописных текстах встречаются первые задачи на проценты. В Древнем Вавилоне, стоявшие на перепутье торговых караванов, рано появились денежные знаки и кредит. Начисляли обычно 12 на 60, т.е. пятую часть, или, говоря современным языком 20%.
Слово «проценты» появилось в Европе, когда итальянские ростовщики, использующие десятичную систему счисления, стали начислять рост долга на сто единиц кредита. Скажем, начисляли 20 на 100, т. е. 20%.
Большое число арифметических задач содержит «Книга абака» итальянского ученого Леонардо Пизанского. Его задачи вплоть до наших дней переходят из одного учебника в другой.
Леонардо, известный также под именем Фибоначчи был первым ученым Западной Европы, освоившим все достижения математиков стран ислама и продвинувшимся дальше них. Он родился в Пизе, крупном торговом городе Италии того времени. Путешествуя по Египту, Сирии, Индии, Сицилии, везде знакомился с правилами счета.
Под словом «абак» Леонардо подразумевает не счетную доску, а арифметику вообще. Его книга учит производить операции с целыми числами и с обыкновенными дробями. В ней изложены приемы решения задач коммерческой арифметики, задач на сплавы. Вот одна из задач.
30 птиц стоят вместе 30 монет. Куропатки — по 3 монеты, голуби — по две монеты, а воробьи — по монете за пару птиц.
Решение, разумеется, разыскивается в целых положительных числах. Леонардо приводит единственное решение такого вида: 3 куропатки, 5 голубей, 22 воробья.
В «Книге абака» впервые появились задачи о наименьшем числе гирь, с помощью которых можно взвесить все целые веса, меньшие некоторого данного. Леонардо так формулирует задачу: выбрать пять гирь так, чтобы с их помощью можно было взвесить любой груз до 30 кг при условии, что гири ставятся на одну чашку весов.
В учебной литературе арифметические задачи всегда занимали большое место. Для тренировки учащихся их часто давали в занимательной форме.
Математик и педагог Л. Ф. Магницкий в книге «Арифметика, сиречь наука числительная» собрал большое число задач. Леонтий Филиппович родился в Тверской губернии, окончил Славяно-греко-латинскую академию. С 1701 г. работал в Школе математических и навигационных наук, которая была организована в Москве по указу Петра 1. «Арифметика» Магницкого широко использовалась в учебных заведениях России в течение полувека. По ней учился М. В. Ломоносов. Он назвал ее «вратами своей учености».
В 1725 г. в Петербурге открылись Академия наук с университетом и гимназией. Молодой швейцарец Леонард Эйлер был приглашен в Россию. Став впоследствии крупнейшим математиком, он написал большое число учебников, в том числе «Руководство к арифметике» и «Универсальную арифметику» (1769). Они стали основой для большинства последующих учебников.
Таким образом, мы видим на сколько велик был труд многих древних ученых, открывших и донесших до наших дней то, без чего нельзя увидеть смысл и дух настоящей математики.
Но задания из выше приведенных книг методической литературы применимы лишь на занятиях для школьников среднего и старшего звена.
Использование на уроках и внеклассных занятиях по математике элементов из ее истории является не только эффективным средством развития интереса учащихся к предмету, но также имеет познавательное и воспитательное значение.
Однако освещать историю развития изучаемых в начальных классах математических понятий на уроках не представляется возможным. Можно сообщать лишь некоторые сведения из истории математики. Один из эффективных методов проведения такой работы – решение на уроках или внеклассных занятиях старинных задач.
В огромном мире пособий для учителей начальных классов не так уж много оригинальных материалов исторического характера, направленных на формирование интереса детей и развитию их познавательной активности. Проанализируем некоторые из них.
Перед нами книга И.Г. Сухина «Занимательные материалы», которая восполняет этот пробел. Здесь можно найти множество занимательных математических задач, имеющие новые решения. Среди них: задачи с дополнительными условиями и подсказками, головоломки с одинаковыми и неповторяющимися цифрами, старинные математические фокусы и многое другое (см. Приложение). Для каждого из четырех классов начальной школы приведены соответствующие задания. При этом автор данной книги постарался не сковывать инициативу учителей, поэтому формы использования публикуемых могут быть самыми разнообразными.
Следующая книга «Старинные занимательные задачи» под редакцией Олесник С.Н., Нестеренко Ю.В., Потапова М.К. в ней собраны 170 занимательных задач, из русских рукописей и книг, опубликованных до 1800-го года (см. Приложение). Книга разделена на три части. В первую часть вошли задачи из рукописей и из книги Л.Ф. Магницкого «Арифметика». Во вторую часть - задачи из учебников, опубликованных в России после издания книги Магницкого, но до 1800-го года. В третью часть - задачи из книг (последнего десятилетия XVIII века), целиком либо в значительной степени посвященных занимательным задачам.
Каждая часть состоит из разделов. Разделы внутри части расположены в порядке возрастания трудностей.
Многие задачи подвергались стилистической обработке.
В оглавлении после названия каждой задачи в скобках указаны два числа: первое из них - номер страницы книги, на которой приведен текст задачи, второе - номер страницы, на котором приведено ее решение.
Как правило, задачи решаются с привлечением минимальных сведений из арифметики, алгебры и геометрии, но требуют сообразительности и умения логически мыслить.
А вот знаменитая книга В.Д. Чистикова «Старинные задачи по элементарной математике» - это сборник старинных задач, включающий задачи Вавилона, Египта, Греции, Китая, Индии, арабские и русские задачи, а также задачи Западное Европы. Состоит из двух частей: первая - тексты задач, вторая - исторические экскурсы, решения и указания. Все исторические сведения решения старинных задач даются в модернизированном виде с широким использованием общепринятой символики. Книга может быть полезна учителю и учащимся.
Большинство задач собранных в этих книгах оригинальны, но не все: некоторые из них общеизвестные. Но тем не менее, они являются методической базой для учителя начальной школы. Эти задачи, позволяют повысить интерес к решению задач младшими школьниками, заставят проявить их интеллектуальные способности.
Литература
1. Баврин И.И., Фрибус Е.А. Занимательные задачи по математике. М, 1999.
2. Баврин И.И., Фрибус Е.А. Старинные задачи. М., 1994.
3. Бантова Н.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах: Учебное пособие для учащихся школ. Отделений пед.училищ. (Спец. № 2001)/Под ред. М.А. Байтовой - 3 изд., испр. - М.: Просвещение, 1984. - 335с, ил.
4. Белов В.Н. Головоломки из близкой дали.//Компьютерра 2000 №1.
5. Депнан И.Я. История арифметики. М, 1965.
6. Леман И. Увлекательная математика. М., 1985.
7. Нестеренко Ю.В., Олесник С.Н., Потапов М.К. Старинные занимательные задачи. - 2-е изд., испр. - М: Наука. Главная редакция физико-математической литературы, 1988. - 160 с.
8. Питерсон Л.Г. Математика, 1 класс, часть третья. - М.: «Баллас», «С - инфо», 2000. - 96с, ил.
9. Попов Г.Н. Сборник исторических задач по элементарной математике. М. - Л.: Главная редакция научно популярной и юношеской литературы, 1938.
10. Сухин И.Г. Занимательные материалы: начальная школа. - М.: ВАКО, 2004. - 240 с. (Мастерская учителя).
11. Чистяков В.Д. Старинные задачи по элементарной математике. - 3-е изд., испр. - Минск: «Высшейшая школа», 1978. - 272 с.
12. Штейнгаус Г. Сто задач: пер. с польск. - 3-е изд., стереотипн. - М.: Наука, 1982, 168 с.
Приложение
Г. Сухин. «Занимательные материалы».
1. Числовые горизонтали с пустыми клетками. (Задачи с дополнительными условиями) с. 11.
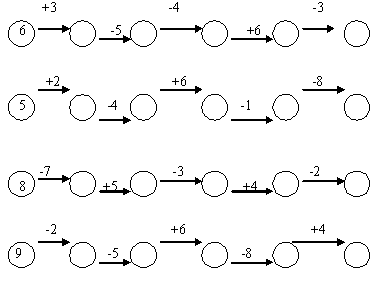
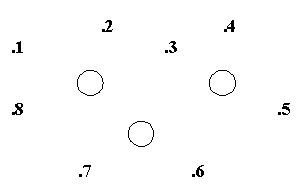
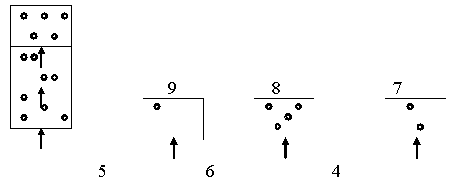
В следующих задачах - равенствах в пустые клетки нужно поместить такие цифры, чтобы примеры были решены правильно. При этом в одной клетке должна быть только одна цифра. 1.
| 9 | + | = | 0 | + |
| - | 4 | = | 5 | + |
Здесь нет одинаковых цифр.
| 9 | + | — | 1 | + |
Похожие работы
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
... . Попробуем это сделать, привлекая на помощь сведения из истории развития образовательно-воспитательных систем и современные приметы использования игры в учебной и воспитательной работе. 1.2. Дидактическая игра, как средство активизации познавательной деятельности младших школьников. В отличие от других видов деятельности игра содержит цель в самой себе; посторонних и отделенных задач в игре ...
... функционируют взаимосвязано, то воздействие на память, внимание и мышление, будет отражаться на познавательной активности младшего школьника.Глава 2. Учреждение дополнительного образования как субъект современного образования. § 1. О становлении и развитии системы дополнительного образования. В 1918 г. в Москве, в Сокольниках, открылось первое государственное внешкольное детское учреждение – ...
... позволяют организовать общение учащихся на более высоком уровне, вызывать у них потребность в обмене информацией, оказании помощи товарищу. Глава 2. Роль уроков информатики в развитии познавательной активности младших школьников В данной главе рассматриваются условия, способы и приемы, способствующие развитию познавательной активности младших школьников на уроках информатики, выделяются ...
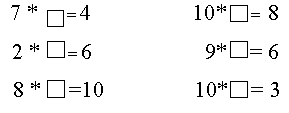
0 комментариев