Диаграмма состояния Mn-Si. Химические и фазовые равновесия в системе Mn-Si
Термодинамическое моделирование свойств твердых металлических растворов. Обобщенная теория «регулярных» растворов
Термодинамические функции образования интерметаллидов
Термодинамические функции бинарных соединений (интерполяционная формула Лагранжа)
Фазовые диаграммы систем Mn-O и Si-O
Расчёт термодинамических функций силицидов марганца по интерполяционной формуле Лагранжа
Моделирование фазовых равновесий в системе Mn – Si
Навигация
Термодинамическое моделирование свойств твердых металлических растворов. Обобщенная теория «регулярных» растворов
Термодинамика химической устойчивости сплавов системы Mn-Si
45983
знака
12
таблиц
7
изображений
1.3 Термодинамическое моделирование свойств твердых металлических растворов. Обобщенная теория «регулярных» растворов
Твёрдые растворы - однородные (гомогенные) кристаллические фазы переменного состава; образуются в двойных или многокомпонентных системах. Если компоненты системы неограниченно растворимы друг в друге, они образуют непрерывный ряд твёрдых растворов. Чаще, однако, концентрация растворенного вещества не может превышать некоторое предельное значение и существование твёрдого раствора ограничено некоторыми областями составов (области гомогенности). Твёрдыми растворами являются многие металлические сплавы и неметаллические системы - минералы, стекла, полупроводники, ферриты [3].
Регулярный раствор образуется из компонентов с выделением или поглощением тепла, а энтропия смешения его такая же, как и в совершенном растворе. Проблема аналитического представления концентрационной и температурной зависимости термодинамических свойств сводится к поиску соответствующего выражения для избыточной энергии Гиббса GE.Обычно в качестве нулевого приближения к теории реальных растворов применяется модель идеального раствора, где GE=0. В настоящей модели за нулевое приближение принята теория регулярных растворов.
Понятие «регулярный раствор» включает в себя как частные случаи понятия «идеальный» и «предельно разбавленный» раствор, а закон граничной регулярности, согласно которому любой раствор можно считать регулярным до определенного предела, справедлив для более широкого диапазона концентраций, чем законы Рауля и Генри.
Для регулярного раствора:
, (1.1)
где xi и xj – мольные доли компонентов,
Qij - энергия взаимообмена (смешения).
В рамках модели строго регулярного раствора энергии взаимообмена являются константами. В реальных системах энергии взаимообмена (как эмпирические параметры модели) зависят от состава и температуры.
Для субрегулярных растворов:
; (1.2)
Для квазирегулярных растворов:
; (1.3)
где: 
и 
- соответственно теплота и избыточная энтропия смешения компонентов. Выражения (1.2) и (1.3), очевидно, можно рассматривать как частные случаи неизвестной функции для концентрационной и температурной зависимостей энергии смешения компонентов, получаемой путем разложения 
и 
в ряд Тейлора. Если ограничиться несколькими первыми членами ряда:
; (1.4)
то получится представление функции полиномом. В свою очередь, каждый из параметров 
, 
, 
,…, 
может зависеть от температуры:
; (1.5)
Многочлены (1.4) и (1.5) - приближенное выражение неизвестной функции 
. Качество приближения определяется величиной остатка рядов – той ее части, которая отбрасывается. Чтобы наше приближение удовлетворительно описывало термодинамические свойства раствора, нужно, чтобы остаток был невелик по сравнению с ошибкой экспериментов. Тогда дальнейшее уточнение функции теряет смысл.
Как показывает математическая обработка экспериментальных данных, для бинарных растворов достаточно трех параметров , , , чтобы в большинстве случаев корректно аппроксимировать термодинамические функции смешения системы.
Поэтому концентрационную (конфигурационную) энергию взаимообмена компонентов в дальнейшем будем представлять тремя членами ряда (1.4), а избыточную энергию Гиббса любой фазы с областью гомогенности будем описывать уравнением:
; (1.6)
где и - термодинамические характеристики областей регулярности двойной системы вблизи чистых компонентов;
- параметр, учитывающий отклонение от «регулярности».
Умножив части уравнения (1.6) на общее число молей 
компонентов в растворе, получим избыточную энергию Гиббса 
произвольного количества фазы. Откуда:
(1.7)
Активности компонентов двойной системы:
; (1.8)
; (1.9)
Обобщенная теория «регулярных» растворов позволяет успешно описать термодинамические свойства металлических, неметаллических и смешанных систем [4].
Похожие работы
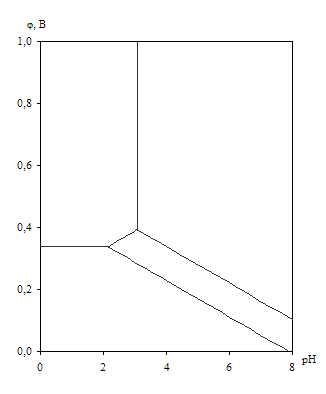
... устойчивость металлов и сплавов определяется их стойкостью к коррозии в водной среде. Лучшим способом представления термодинамической информации о химической и электрохимической устойчивости металлических систем в водных растворах являются диаграммы рН-потенциал. Впервые такие диаграммы в системе элемент-вода для чистых металлов при температуре 250С были построены Марселем Пурбе и использованы им ...
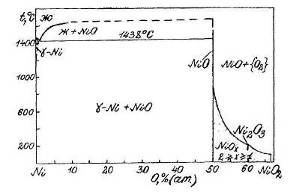
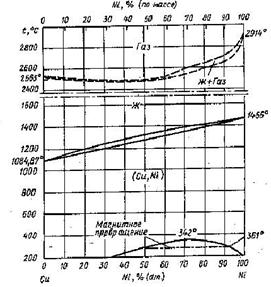
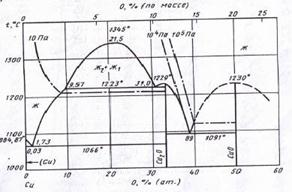
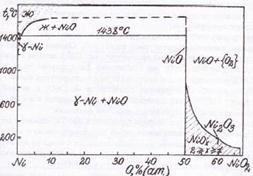
... VIII – CuO + NiO2 + {O2}. Области I и V очень малы и в масштабе диаграммы вырождаются в линии. Анализируя диаграмму Cu – Ni – O можно сделать следующие выводы о химической устойчивости медно-никелевых сплавов: 1) Окисление сплавов начинается уже при давлениях кислорода в газовой фазе над сплавами большем чем атм. Поэтому медно-никелевые сплавы будут окисляться кислородом воздуха при 25оС. 2) ...
... пособие по прикладной химии «Задачи по теоретическим основам химической технологии», составленное по материалам представленной работы. 3. Методика решения задач по теоретическим основам химической технологии Одна из главных задач химической науки и промышленности - получение необходимых человеку веществ (продуктов, материалов). Поэтому большинство учебных химических задач снизано с ...
абсолютно чистые минералы, расплавленные и сублимированные горные породы. Гетерогенной это такая термодинамическая система, которая состоит из двух и более гомогенных областей. Внутри такой системы имеются поверхности раздела фаз, при переходе через которые химический состав и физические свойства вещества изменяются скачкообразно. Фазой гетерогенной системы называется гомогенная область, которая ...
0 комментариев