Моделирование фазовых равновесий в системе Mn – Si

2.4 Моделирование фазовых равновесий в системе Mn – Si

Для описания термодинамических свойств фаз переменного состава твердых растворов применялась обобщенная теория «регулярных» растворов в однопараметрическом приближении.

Уравнение реакции, соответствующее образованию R- фазы:

 (1)

 (2)

 (3)

Энергии Гиббса реакций 2 и 3 описываются уравнениями температурной зависимости:

Энергия Гиббса реакции 1 может быть найдена комбинированием энергий Гиббса реакций 2 и 3:

***

Активности компонентов системы рассчитываем по формулам:

,

где  .

«Кажущиеся» энергии смешения описываем уравнением температурной зависимости:

С учётом () уравнения () и () преобразуются:

 *

**

Уравнение изотермы для химической реакции (1):

Константа равновесия реакции (1):

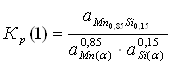
С учётом формул * и ** уравнение ***:

Пусть , тогда:

Преобразуем:

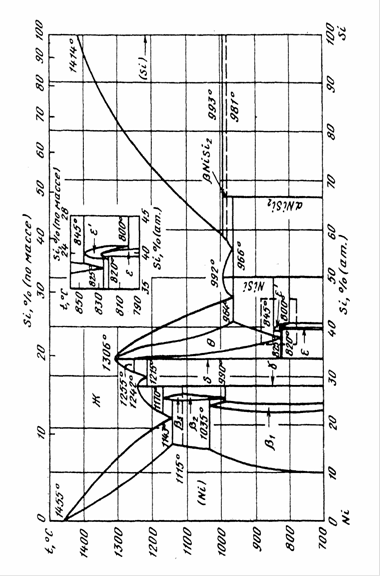
Задача сводится к нахождению неизвестных параметров уравнения Необходимые для расчетов мольные доли кремния, соответствующие равновесию α-фазы с Mn0,85Si0,15 при различных температурах получили из диаграммы состояния Mn – Si.

Табл. 2.5. Мольные доли кремния при различных температурах.

Т, К	473	523	573	623	673	723	773	823	873	903
х (Si)	0,0483	0,0500	0,0510	0,0515	0,0530	0,0550	0,0565	0,0590	0,0610	0,0625

Таким образом, получается система из 10 уравнений с 4 неизвестными параметрами  Учитывая, что Дж/моль, то вводится дополнительное 11 уравнение

Для решения этой системы использован метод Крамера. По данному методу для системы n линейных уравнений с n неизвестными

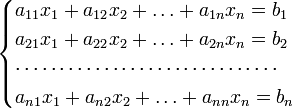
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

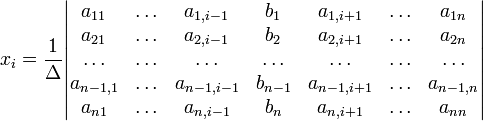
После решения данной системы найдены неизвестные параметры :

, , ,

Далее проведена подстановка полученных значений параметров в исходную систему уравнений и установлена адекватность полученных значений.

При Т=298 К определена точка предельной растворимости кремния в альфа-марганце:

По уравнениям ……находим активности компонентов системы в точке предельной растворимости кремния в альфа-марганце:

,

Таким образом, исходя из полученных результатов, можно прийти к заключению, что в области низких температур (вплоть до комнатной) кремний практически не растворяется в марганце.

2.5  . Расчет и построение диаграммы состояния Mn-Si-O при 250С. Анализ химической устойчивости

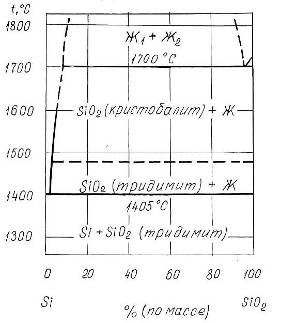
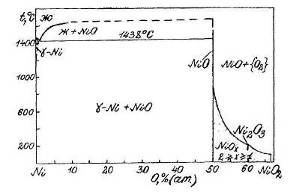
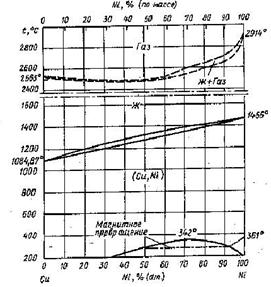
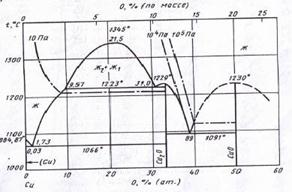
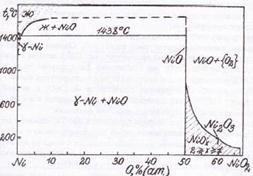
Как следует из экспериментальных данных по системе марганец-кремний (рис.1.1), кремний-кислород (рис.1.4) и марганец-кислород (рис.1.5) в системе Mn-Si-O можно предположить существование областей, в которых присутствуют следующие фазы (поскольку химическое сродство кремния к кислороду выше, чем марганца, то вероятнее, что почти при любом составе сплава Mn-Si в первую очередь будет реализовываться равновесие сплав – SiO2):

1.  Si(γ) – Mn11Si19 – SiO2; (I)

2.  Mn11Si19 – MnSi –SiO2; (II)

3.  MnSi – Mn5Si3 – SiO2; (III)

4.  Mn5Si3 – Mn5Si2 – SiO2; (IV)

5.  Mn5Si2– Mn3Si – SiO2; (V)

6.  Mn3Si – Mn9Si2 – SiO2; (VI)

7.  Mn9Si2 – R(Mn6Si) – SiO2; (VII)

8.  R(Mn6Si) – α-фаза – SiO2; (VIII)

9.  α-фаза – SiO2; (IX)

10.  α-фаза ––MnSiO3–SiO2; (X)

11.  α-фаза ––Mn2SiO4–MnSiO3; (XI)

12.  α-фаза ––MnO– Mn2SiO4; (XII)

13.  MnO–Mn3O4– Mn2SiO4; (XIII)

14.  Mn3O4– Mn2SiO4– MnSiO3; (XIV)

15.  Mn3O4–Mn2O3– MnSiO3; (XV)

16.  Mn2O3– MnSiO3–SiO2; (XVI)

17.  Mn2O3–MnO2–SiO2; (XVII)

18.  MnO2–Mn2O7–SiO2; (XVIII)

19.  Mn2O7–SiO2–{O2}; (XIX)

Для того, чтобы однозначно определить инвариантное состояние системы, необходимо задать равновесные составы сосуществующих фаз и давление кислорода в газовой фазе, равновесной с конденсированными фазами.

Примеры расчета:

а) Фазовое равновесие V: Mn5Si2– Mn3Si – SiO2

Уравнение реакции, соответствующее данному равновесию:

 (1)

Константа равновесия реакции (1):

; (2.1)

Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

; (2.2)

Уравнение изотермы химической реакции:

; (2.3)

Энергия Гиббса реакции (1) рассчитывается по формуле:

; (2.4)

С учетом уравнения (2.2):

б) Фазовое равновесие X:

α-фаза ––MnSiO3–SiO2 было описано независимыми реакциями образования SiO2 и MnSiO3 из компонентов α-фазы (Mn, Si) и компонентов газовой фазы O2:

(1) ;

(2) ;

Константы равновесия реакций 1 и 2:

; (2.3)

; (2.4)

Для определения состава α-фазы исключим  из конечного термодинамического уравнения. Для этого возведем уравнение (2.3) в куб и поделим полученное на уравнение (2.4), получим:

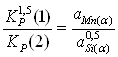; (2.5)

Это уравнение можно переписать в виде:

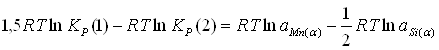; (2.6)

Из уравнения изотермы химической реакции:

; (2.7)

уравнение (2.3.4) можно переписать:

; (2.8)

Данное трансцендентное уравнение можно решить только численным методом. Обозначив , , получим:

; (2.9)

; (2.10)

Подставив уравнения (2.9) и (2.10) в (2.8) решаем численным методом, находим значение х. Исходя из уравнений (2.3) или (2.4) определяем величину .

Полученные результаты сведены в таблице 2.6.

Табл.2.6 Характеристики фазовых равновесий системы Mn-Si-O при 25 0С

Состояние	Уравнение реакции
Si – Mn11Si19 – SiO2	Si(A) + O2 = SiO2	805067	7,7e-142
Mn11Si19 – MnSi –SiO2	Mn11Si19 + 8O2 = 11MnSi + 8SiO2	789464	4,18E-139
MnSi – Mn5Si3 – SiO2	5MnSi + 2O2 = Mn5Si3 + 2SiO2	757015	2,04E-133
Mn5Si3 – Mn5Si2 – SiO2	Mn5Si3 + O2 = Mn5Si2 + SiO2	742497	7,14E-131
Mn5Si2– Mn3Si – SiO2	3Mn5Si2 + O2 = 5Mn3Si + SiO2	739167	2,74E-130
Mn3Si – Mn9Si2 – SiO2	3Mn3Si + O2 = Mn9Si2 + SiO2	736728	7,33E-130
Mn9Si2 – Mn6Si – SiO2	2Mn9Si2 + O2 = 3Mn6Si + SiO2	702737	1,99E-129
Mn6Si – α – SiO2 xSi(α)=0,0361; aMn(α)=0,91	Mn6Si + O2 = 6Mn(α) + SiO2	693587	3,77E-122
α – SiO2	Si(α)+O2=SiO2 Mn(α)+Si(α)+1,5O2=MnSiO3
α ––MnSiO3–SiO2			2,3Е-128
α ––Mn2SiO4–MnSiO3	-	-	-
α ––MnO– Mn2SiO4	-	-	-
MnO–Mn3O4– Mn2SiO4	6MnO + O2 = 2Mn3O4	387290	1,3E-68
Mn3O4– Mn2SiO4– MnSiO3	6Mn2SiO4 + O2 = 6MnSiO3 + 2Mn3O4	375710	1,4E-66
Mn3O4–Mn2O3– MnSiO3	4Mn3O4 + O2 = 6Mn2O3	147860	1,21E-26
Mn2O3–MnO2–MnSiO3	2Mn2O3 + O2 = 4MnO2	102920	9,1E-19
MnO2 – MnSiO3 – SiO2	2MnSiO3 + O2 = 2MnO2 + 2SiO2	200474	7,25E-36
MnO2–Mn2O7–SiO2	4MnO2 + 3O2 = 2Mn2O7	1335600	1,09E+78
Mn2O7–SiO2–{O2}

кремний марганец термодинамический химический равновесие

Рассчитать равновесия 10-12 не представляется возможным, что может свидетельствовать о том, что какой-либо из силицидов окисляется до силиката раньше, чем α-фаза. С этим же может быть связана и неупорядоченная последовательность вычисленных значений Р(О2).

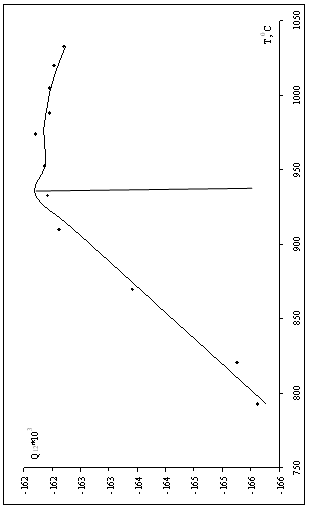
Для того, чтобы показать термодинамическую возможность или невозможность осуществления реакций между оксидами марганца и кремния в равновесии с альфа-фазой, выполнены следующие расчёты. Для каждой из возможных реакций вычислен интервал значений Q12, удовлетворяющий условию возможности протекания этой реакции при в области составов системы Mn – Si, при которой альфа-фаза термодинамически устойчива.

1)

;

;

;

.

2)

;

;

;

.

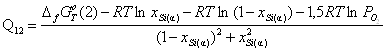3)

;

;

;

.

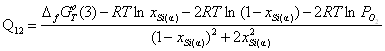4)

;

;

;

.

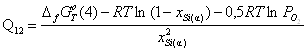При оценке параметров Q12 необходимо учесть следующие условия: а) мольная доля кремния в альфа-фазе должна находиться в пределах существования альфа-фазы – ; б) давление кислорода в газовой фазе над конденсированной фазой не должно быть больше значения, при котором возможно окисление чистого марганца – атм. Подставляя в выражения для энергий смешения значения энергий Гиббса реакций (1) – (4), получаем следующие неравенства:

Для реакции (1): ,

Для реакции (2): ,

Для реакции (3): ,

Для реакции (4): .

Сравнивая между собой полученные значения Q12, можно прийти к выводу о том, что протекание реакций между оксидами марганца и кремния в равновесии с альфа-фазой невозможно.

Таким образом, предположение о том, что окисление SiO2 до MnSiO3, MnSiO3 до Mn2SiO4, Mn2SiO4 до MnO реализуются в равновесии с альфа-фазой, не подтвердилось. Поэтому необходимо проверить предположение о том, что вышеуказанные реакции реализуются в равновесии с одним из силицидов марганца. Для этого были рассмотрены все возможные трёхфазные равновесия в системе Mn-Si-O, которые представлены в таблице.

Табл. 2.7 Все возможные трёхфазные равновесия в системе Mn-Si-O

Состояние	Уравнение реакции
Si – Mn11Si19 – SiO2	Si(A) + O2 = SiO2
Mn11Si19 – MnSi –SiO2	Mn11Si19 + 8O2 = 11MnSi + 8SiO2
MnSi – Mn5Si3 – SiO2	5MnSi + 2O2 = Mn5Si3 + 2SiO2
Mn5Si3 – Mn5Si2 – SiO2	Mn5Si3 + O2 = Mn5Si2 + SiO2
Mn5Si2– Mn3Si – SiO2	3Mn5Si2 + O2 = 5Mn3Si + SiO2
Mn3Si – Mn9Si2 – SiO2	3Mn3Si + O2 = Mn9Si2 + SiO2
Mn9Si2 – Mn0,85Si0,15 – SiO2	17Mn9Si2 + 7O2 = 180Mn0,85Si0,15 + 7SiO2
Mn0,85Si0,15 – α – SiO2 xSi(α)=0,042; aMn(α)=0,855	20Mn0,85Si0,15 + 3O2 = 17Mn(α) + 3SiO2
=================	=================
Mn11Si19 – SiO2 – MnSiO3	2Mn11Si19 + 49O2 = 22MnSiO3 + 16SiO2
MnSi – SiO2 – MnSiO3	2MnSi + 0SiO2 + 3O2 = 2MnSiO3
Mn5Si3 – SiO2 – MnSiO3	2Mn5Si3 + 4SiO2 + 11O2 = 10MnSiO3
Mn5Si2 – SiO2 – MnSiO3	2Mn5Si2 + 6SiO2 + 9O2 = 10MnSiO3
Mn3Si – SiO2 – MnSiO3	2Mn3Si + 4SiO2 + 5O2 = 6MnSiO3
Mn9Si2 – SiO2 – MnSiO3	2Mn9Si2 + 14SiO2 + 13O2 = 18MnSiO3
Mn0,85Si0,15 – SiO2 – MnSiO3	40Mn0,85Si0,15 + 28SiO2 + 23O2 = 34MnSiO3
==================	=================
Si – Mn11Si19 – MnSiO3	2Mn11Si19 + 33O2 = 22MnSiO3 + 16Si
Mn11Si19 – MnSi – MnSiO3	0Mn11Si19 + 2MnSi + 3O2 = 2MnSiO3
MnSi – Mn5Si3 – MnSiO3	2MnSi + 3O2 = 0Mn5Si3 + 2MnSiO3
Mn5Si3 – Mn5Si2 – MnSiO3	6Mn5Si3 + 15O2 = 4Mn5Si2 + 10MnSiO3
Mn5Si2– Mn3Si – MnSiO3	4Mn5Si2 + 3O2 = 6Mn3Si + 2MnSiO3
Mn3Si – Mn9Si2 – MnSiO3	14Mn3Si + 9O2 = 4Mn9Si2 + 6MnSiO3
Mn9Si2 – Mn0,85Si0,15 – MnSiO3	4Mn9Si2 + 3O2 = 40Mn0,85Si0,15 + 2MnSiO3
Mn0,85Si0,15 – α – MnSiO3 xSi(α)=0,042; aMn(α)=0,855	40Mn0,85Si0,15 + 9O2 = 28Mn(α) + 6MnSiO3
==================	=================
Mn11Si19 – MnSiO3 – Mn2SiO4	2Mn11Si19 + 16Mn2SiO4 + 49O2 = 54MnSiO3
MnSi – MnSiO3 – Mn2SiO4	2MnSi + 3O2 = 0Mn2SiO4 + 2MnSiO3
Mn5Si3 – MnSiO3 – Mn2SiO4	2Mn5Si3 + 11O2 = 2MnSiO3 + 4Mn2SiO4
Mn5Si2 – MnSiO3 – Mn2SiO4	2Mn5Si2 + 2MnSiO3 + 9O2 = 6Mn2SiO4
Mn3Si – MnSiO3 – Mn2SiO4	2Mn3Si + 2MnSiO3 + 5O2 = 4Mn2SiO4
Mn9Si2 – MnSiO3 – Mn2SiO4	2Mn9Si2 + 10MnSiO3 + 13O2 = 14Mn2SiO4
Mn0,85Si0,15 – MnSiO3 – Mn2SiO4	40Mn0,85Si0,15 + 22MnSiO3 + 23O2 = 28Mn2SiO4
==================	=================
Si – Mn11Si19 – Mn2SiO4	2Mn11Si19 + 22O2 = 27Si + 11Mn2SiO4
Mn11Si19 – MnSi – Mn2SiO4	27MnSi + 16O2 = Mn11Si19 + 8Mn2SiO4
MnSi – Mn5Si3 – Mn2SiO4	Mn5Si3 + 4O2 = MnSi + 2Mn2SiO4
Mn5Si3 – Mn5Si2 – Mn2SiO4	Mn5Si3 + Mn5Si2 + 10O2 = 5Mn2SiO4
Mn5Si2– Mn3Si – Mn2SiO4	Mn5Si2 + 2O2 = Mn3Si + Mn2SiO4
Mn3Si – Mn9Si2 – Mn2SiO4	5Mn3Si + 6O2 = Mn9Si2 + 3Mn2SiO4
Mn9Si2 – Mn0,85Si0,15 – Mn2SiO4	11Mn9Si2 + 14O2 = 100Mn0,85Si0,15 + 7Mn2SiO4
Mn0,85Si0,15 – α – Mn2SiO4 xSi(α)=0,042; aMn(α)=0,855	20Mn0,85Si0,15 + 6O2 = 11Mn(α) + 3Mn2SiO4
==================	=================
Mn11Si19 – Mn2SiO4 – MnO	2Mn11Si19 + 54MnO + 49O2 = 38Mn2SiO4
MnSi – Mn2SiO4 – MnO	2MnSi + 2MnO + 3O2 = 2Mn2SiO4
Mn5Si3 – Mn2SiO4 – MnO	2Mn5Si3 + 2MnO + 11O2 = 6Mn2SiO4
Mn5Si2 – Mn2SiO4 – MnO	2Mn5Si2 + 9O2 = 4Mn2SiO4 + 2MnO
Mn3Si – Mn2SiO4 – MnO	2Mn3Si + 5O2 = 2Mn2SiO4 + 2MnO
Mn9Si2 – Mn2SiO4 – MnO	2Mn9Si2 + 13O2 = 4Mn2SiO4 + 10MnO
Mn0,85Si0,15 – Mn2SiO4 – MnO	40Mn0,85Si0,15 + 23O2 = 6Mn2SiO4 + 22MnO
==================	=================
Si – Mn11Si19 – MnO	2Mn11Si19 + 11O2 = 38Si(A) + 22MnO
Mn11Si19 – MnSi – MnO	19MnSi + 4O2 = Mn11Si19 + 8MnO
MnSi – Mn5Si3 – MnO	Mn5Si3 + O2 = 3MnSi + 2MnO
Mn5Si3 – Mn5Si2 – MnO	6Mn5Si2 + 5O2 = 4Mn5Si3 + 10MnO
Mn5Si2– Mn3Si – MnO	4Mn3Si + O2 = 2Mn5Si2 + 2MnO
Mn3Si – Mn9Si2 – MnO	2Mn9Si2 + 3O2 = 4Mn3Si + 6MnO
Mn9Si2 – Mn0,85Si0,15 – MnO	80Mn0,85Si0,15 + 7O2 = 6Mn9Si2 + 14MnO
Mn0,85Si0,15 – α – MnO xSi(α)=0,042; aMn(α)=0,855	2Mn(α) + O2 = 2MnO
==================	=================
MnO – Mn3O4 – Mn2SiO4	6MnO + O2 = 2Mn3O4
Mn3O4 – Mn2SiO4 – MnSiO3	6Mn2SiO4 + O2 = 6MnSiO3 + 2Mn3O4
Mn3O4 – Mn2O3 – MnSiO3	4Mn3O4 + O2 = 6Mn2O3
Mn2O3 – MnO2 – MnSiO3	2Mn2O3 + O2 = 4MnO2
MnO2 – MnSiO3 – SiO2	2MnSiO3 + O2 = 2MnO2 + 2SiO2
MnO2 – Mn2O7 – SiO2	4MnO2 + 3O2 = 2Mn2O7
Mn2O7 – SiO2 – {O2}

Задача состоит в том, чтобы подобрать последовательность равновесий, которая бы удовлетворяла условию возрастания давления кислорода в системе. При этом возможно проводить варьирование значений энергий Гиббса образования силицидов в пределах возможных справочных значений.

После многократного согласования энергий Гиббса образования силицидов, взятых из различных источников, получен следующий вариант последовательности окисления.

1.  Si – Mn11Si19 – SiO2; (I)

2.  Mn11Si19 – MnSi – SiO2; (II)

3.  MnSi– Mn5Si3– SiO2; (III)

4.  Mn5Si3 – MnSiO3– SiO2; (IV)

5.  Mn5Si3 – MnSiO3 – Mn2SiO4; (V)

6.  Mn5Si3 – Mn5Si2 – Mn2SiO4; (VI)

7.  Mn5Si2– Mn3Si – Mn2SiO4; (VII)

8.  Mn3Si –Mn2SiO4 – MnO; (VIII)

9.  Mn9Si2 – Mn3Si – MnO; (IX)

10.  Mn0,85Si0,15 – Mn9Si2 – MnO; (X)

11.  α – Mn0,85Si0,15– MnO; (XI)

12.  MnO – Mn3O4 – Mn2SiO4; (XII)

13.  Mn3O4 – Mn2SiO4 – MnSiO3; (XIII)

14.  Mn3O4 – Mn2O3 – MnSiO3; (XIV)

15.  Mn2O3 – MnO2 – MnSiO3; (XV)

16.  MnO2 – MnSiO3 – SiO2; (XVI)

17.  MnO2 – Mn2O7 – SiO2; (XVII)

18. Mn2O7–SiO2–{O2}; (XVIII)

Примеры расчета:

а) Фазовое равновесие III: MnSi– Mn5Si3 – SiO2

Уравнение реакции, соответствующее данному равновесию:

 (1)

Константа равновесия реакции (1):

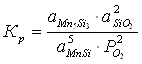; (2.1)

Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

; (2.2)

Уравнение изотермы химической реакции:

; (2.3)

Энергия Гиббса реакции (1) рассчитывается по формуле:

; (2.4)

С учетом уравнения (2.2):

б) Фазовое равновесие X:

Mn0,85Si0,15 – Mn9Si2 – MnO

Уравнение реакции, соответствующее данному равновесию:

80Mn0,85Si0,15 + 7O2 = 6Mn9Si2 + 4MnO

Константа равновесия реакции (2):

;

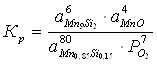Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

;

Дальнейшие расчёты аналогичны предыдущему.

в) Фазовое равновесие XI:

α – Mn0,85Si0,15– MnO

Уравнение реакции, соответствующее данному равновесию:

2Mn(α)+O2=2MnO

Константа равновесия реакции (3):

;

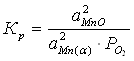Мольная доля чистого вещества равна единице, поэтому выражение для константы равновесия упрощается:

 (4)

Равновесие MnO с альфа-фазой является моновариантным, поэтому давление кислорода в газовой фазе, равновесной с конденсированной фазой, будет зависеть от активности марганца в альфа-фазе. Однозначно определить его можно, например, для точки, соответствующей предельной растворимости кремния в марганце. В этой точке мольная доля кремния , и .

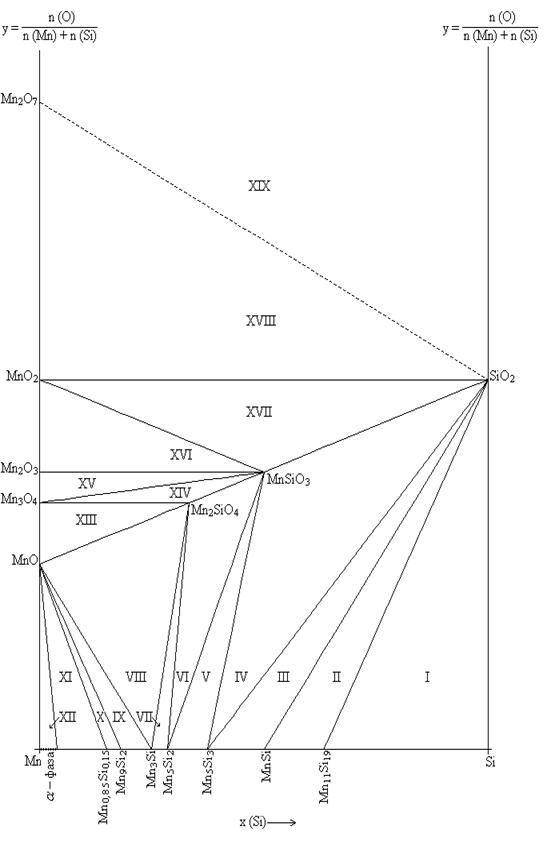
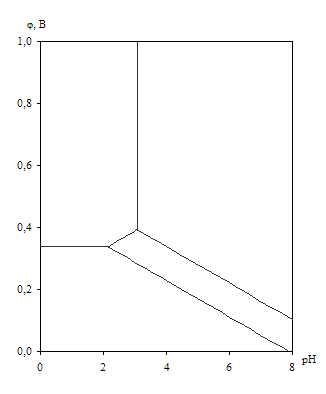
Рис.2.1. Фазовая диаграмма состояния системы Mn-Si-O при 25 0С.

Таблица 2.8 Характеристики фазовых равновесий системы Mn-Si-O при 25 0С

№	Равновесие		Уравнение реакции		, атм.		Равновесный состав фаз
I	Si – Mn11Si19 – SiO2		Si(A) + O2 = SiO2
II	Mn11Si19 – MnSi – SiO2		Mn11Si19 + 8O2 = 11MnSi + 8SiO2
III	MnSi– Mn5Si3– SiO2		5MnSi + 2O2 = Mn5Si3 + 2SiO2
IV	Mn5Si3 – MnSiO3– SiO2		2Mn5Si3 + 4SiO2 + 11O2 = 10MnSiO3
V	Mn5Si3 – Mn5Si2–MnSiO3		6Mn5Si3 + 15O2 = 4Mn5Si2 + 10MnSiO3
VI	Mn5Si2–MnSiO3–Mn2SiO4		2Mn5Si2 + 2MnSiO3 + 9O2 = 6Mn2SiO4
VII	Mn5Si2– Mn3Si – Mn2SiO4		Mn5Si2 + 2O2 = Mn3Si + Mn2SiO4
VIII	Mn3Si –Mn2SiO4 - MnO		2Mn3Si + 5O2 = 2Mn2SiO4 + 2MnO
IX	Mn9Si2 – Mn3Si – MnO		2Mn9Si2 + 3O2 = 4Mn3Si + 6MnO
X	Mn0,85Si0,15–Mn9Si2–MnO		80Mn0,85Si0,15 + 7O2 = 6Mn9Si2 + 4MnO
XI	α – Mn0,85Si0,15– MnO		2Mn(α)+O2=2MnO
XII	α– MnO
XIII	MnO – Mn3O4 – Mn2SiO4		6MnO + O2 = 2Mn3O4
XIV	Mn3O4–Mn2SiO4–MnSiO3		6Mn2SiO4 + O2 = 6MnSiO3 + 2Mn3O4
XV	Mn3O4 – Mn2O3 – MnSiO3		4Mn3O4 + O2 = 6Mn2O3
XVI		Mn2O3 – MnO2 – MnSiO3		2Mn2O3 + O2 = 4MnO2
XVII		MnO2 – MnSiO3 – SiO2		2MnSiO3 + O2 = 2MnO2 + 2SiO2
XVIII		MnO2 – Mn2O7 – SiO2		4MnO2 + 3O2 = 2Mn2O7
XIX		Mn2O7–SiO2–{O2}

Список литературы

1.  Гельд П. В., Сидоренко Ф. А. Силициды переходных металлов четвертого периода. М.: Металлургия, 1971. С. 120 – 143.

2.  Диаграммы состояния двойных металлических систем. Под общей ред. Н. П. Лякишева. М.: Машиностроение, 1997-2000. Т. 3 кн.1. С. 361,383,698

3.  «Твёрдые растворы. Химическая энциклопедия»

http://www.xumuk.ru/encyklopedia/2/4329.html

4.  Тюрин А. Г. Термодинамика химической и электрохимической устойчивости сплавов: Учеб. Пособие в 2 ч. Часть 1.Общие принципы. Высокотемпературное окисление. Челябинск: Изд-во ЧелГУ, 2004. 86 с.

5.  «Интерметаллиды. Химическая энциклопедия». 02.06.2009.

http://www.xumuk.ru/encyklopedia/1712.html

6.  Мосунова Т.В. Термодинамика химической и электрохимической устойчивости сплавов системы Co-Si: дипломная работа // рук. Тюрин А.Г. Челябинск, 2001. 56 с.

7.  Тюрин А.Г. Моделирование термодинамических свойств растворов: Учебное пособие; Челябинск: ЧелГУ, 1997. 74 с.

8.  О. Кубашевски. Диаграммы состояния двойных систем на основе железа: справ. изд. / пер. с англ. М.: Металлургия, 1985. С. 175 – 179.

9.  Могутнов Б. М., Томилин И. А., Шварцман Л. А. Термодинамика сплавов железа. М.: Металлургия, 1984. 208 с.

10.  Рузинов Л. П., Гуляницкий Б. С. Равновесные превращения металлургических реакций. М.: Металлургия, 1975. 416 с.

11.  База данных «Термические константы веществ».

12.  Моисеев и др. Температурные зависимости приведённой энергии Гиббса.

13.  Ерёменко и др. Физическая химия неорганических материалов.