Навигация
Непротиворечивость геометрии Лобачевского
2.2 Непротиворечивость геометрии Лобачевского
Выведя уже в своей первой работе «О началах геометрии» формулы тригонометрии своей новой системы, Лобачевский заметил, что «эти уравнения переменяются в … (уравнения) сферической Тригонометрии, как скоро вместо боков а, b, c ставим в а -1, b -1, с -1, но в обыкновенной Геометрии и сферической Тригонометрии везде входят одни содержания ( то есть отношения ) линий: следовательно, обыкновенная Геометрия, Тригонометрия и эта новая геометрия всегда будут согласованы между собой». Это означает, что если мы запишем теорему косинусов, теорему синусов и двойственную теорему косинусов сферической тригонометрии для сферы радиуса r в виде
sinA sinB sinC,
sin(a/r) sin(b/r) sin(c/r)
cos(a/r)=cos(b/r)*cos(c/r)+sin(b/r)*sin(c/r)*cosA,
cosA=-cosBcosC+sinBsinCcos(a/r),
то формулы тригонометрии Лобачевского можно записать в том же виде, заменив стороны а,b,c треугольника произведениями ai, bi, ci; так как умножение сторон а,b,c на i равносильно умножению на i радиуса сферы, то, полагая r=qi и воспользовавшись известными соотношениями
cos(ix) = ch x, sin(ix) = i sh x,
мы можем переписать соответственные формулы тригонометрии Лобачевского в виде
ch(a/q)=ch(b/q)*ch(c/q)-sh(b/q)*sh(c/q)*cosA,
sinA sinB sinC,
sh(a/q) sh(b/q) sh(c/q)
cosA = -cosBcosC + sinBsinCcos(a/q).
Сам Лобачевский пользовался не функциями ch x и sh x, а комбинациями введенной им функции П(х) с тригонометрическими функциями; постоянная q в этих формулах – та же, что и в формулах (1) и (2).
Фактически Лобачевский доказал непротиворечивость своей системы тем, что ввел как на плоскости, так и в пространстве координаты и таким образом построил арифметическую модель плоскости и пространства Лобачевского. Однако сам Лобачевский видел свидетельство непротиворечивость открытой им геометрии в указанной связи формул его тригонометрии с формулами сферической тригонометрии. Этот вывод Лобачевского неправомерен. В своих мемуарах он доказал, что формулы сферической тригонометрии вытекают из его геометрии, между тем, чтобы утверждать, что из непротиворечивости тригонометрических формул вытекает непротиворечивость геометрии Лобачевского, надо было доказать, что все предложения последней можно вывести из ее тригонометрических формул и «абсолютной геометрии» - предложений, не зависящих от пятого постулата. Лобачевский попытался провести такое доказательство, но в его рассуждения вкралась ошибка.
2.3 Модели геометрии Лобачевского
Первой, по времени явилась модель планиметрии Лобачевского на некоторых поверхностях (именно на поверхностях постоянной отрицательной кривизны). На этих поверхностях в смысле их внутренней геометрии, когда расстоянии между точками определяются по кратчайшим линиям на самой поверхности, выполняется геометрия Лобачевского. Только не на всей плоскости, а на той ее части, которая может быть представлена данной поверхностью. Вместе с тем доказано, что не существует (в трехмерном евклидовом пространстве) никакой поверхности, которая своей внутренней геометрией представляла бы плоскость Лобачевского.
Реализацию геометрии Лобачевского на поверхностях установил итальянский математик Бельтрами в 1868 г.
Соответствующие поверхности могут быть изготовлены, и тогда геометрия на кусках плоскости Лобачевского представляется самым реальным способом.
Следующая по времени появления геометрическая модель дается на обычной евклидовой плоскости. В ней вся плоскость Лобачевского представляется внутренностью круга, прямые представлены хордами (с исключенными концами).
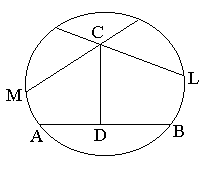
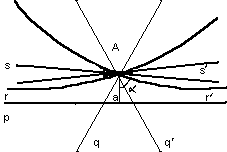
Преобразования – отображения круга на себя, переводящие хорды в хорды, принимаются наложения (движения или перемещения), так что равными считаются фигуры внутри круга, которое отображаются одна на другую при таких преобразованиях круга. (Аксиома параллельных не выполняется: через точку А на рис. проходит бесконечно много «прямых» - хорд, не пересекающих «прямую» а.)
Геометрия Лобачевского в пространстве представляется аналогичной моделью. Пространством служит внутренность шара, прямыми – хорды с исключенными концами, наложениями – отображения шара на себя, переводящие хорды в хорды. Плоскости представляются внутренностью кругов, являющихся плоскими сечениями шара.
Эта модель называется моделью Кэли – Клейна потому, что фактически построил в 1859 г. английский математик Кэли, хотя и не понял, что введенная им геометрия в круге и есть геометрия Лобачевского. Это установил в 1871 г. немецкий математик Клейн.
Таким образом, можно сказать, что геометрия Лобачевского оказывается не более как некоторым фрагментом геометрии Евклида, только изложенным особым образом. Если взять обычный круг, внутренность его называть плоскостью, точки - точками, хорды – прямыми и объявить равными фигуры внутри круга, переводимые одна в другую преобразованиями, при которых круг переходит сам в себя и хорды - в хорды, то это и будет геометрия Лобачевского.
Так многовековые поиски доказательства аксиомы параллельных и немыслимость неевклидовой геометрии разрешились, можно сказать: в некотором пересказе некоторых элементов обычной геометрии внутри круга.
Третья геометрическая модель была дана в 1882 г. французским математиком Пуанкаре. В ней геометрия Лобачевского также представляется некоторым фрагментом геометрии Евклида, только изложенным особым образом (существенно отличным от модели Кэли-Клейна).
Но можно строить аналитическую модель геометрии, представляя точки координатами и выражая расстояние формулой в координатах.
Такую модель геометрии Лобачевского дал немецкий математик Риман в качестве частного случая общей определенной им геометрии, называемой теперь римановой. Риман при вступлении на должность в Геттингенский университет в 1854 г. прочел лекцию «О гипотезах, лежащих в основании геометрии», в которой в общих чертах определил общее понятие пространства любого числа измерений и указал общий принцип введения метрики – измерения расстояний бесконечно малыми шагами. Он также указал возможное значение его теории для физики, как бы предвидя теорию тяготения Эйнштейна.
Однако лекция осталась непонятой и была опубликована только в 1869 г., после смерти Римана.
Когда геометрия Лобачевского достаточно развита, можно на плоскости ввести координаты и дать формулу, выражающую расстояние между точками через их координаты. После этого стоит только перевернуть вывод, заявив: неевклидова геометрия – это теория, в которой точки задаются координатами и расстояния - соответствующей формулой.
Похожие работы
... 3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г. 4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г. Приложение 1 Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря(20 ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...

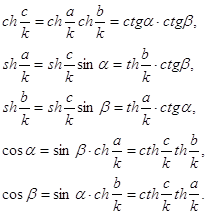
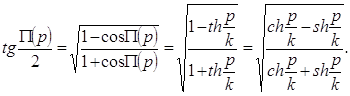
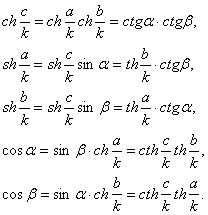
0 комментариев