Навигация
Вопрос о существовании подобных фигур
2. Вопрос о существовании подобных фигур
Перейдем к вопросу о связи постулатов параллельности с вопросом о существовании подобных фигур. Докажем, что существование подобных фигур возможно только в том случае, если справедлив постулат Евклида. Для этого докажем следующую теорему.
Задача 4. Доказать, что если существуют два подобных треугольника, то справедлив постулат Евклида.
Доказательство. Пусть у треугольника АВС и А1В1С1 углы попарно равны:
А=А1, В=В1, С=С1, но сторона АВ>А1В1. На стороне АВ отложим отрезок АВ=АВ и проведем прямую АМ под углом ВАМ=А. Так как АМ не может пересекать прямую АС, то она пересечет отрезок ВС в некоторой точке С. Так как АВС=АВС, то в четырехугольнике ААСС сумма углов равна 4d. Разделяя его диагональю на два треугольника, получим, что в каждом из них сумма углов равна 2d т.е. справедлив постулат Евклида.
3. Основное свойство параллелизма
Лобачевский доказывает, что прямая, параллельная данной прямой в некоторой своей точке, параллельна ей во всех своих точках.
Задача 5. Доказать, что прямая сохраняет признак параллельности во всех своих точках.
Доказательство. Пусть прямая ВВ параллельна в точке Р прямой АА. Рассмотрим точку Q, лежащую от точки Р в сторону параллельности, т.е. по ту же сторону от прямой PR, соединяющей Р с некоторой точкой R на АА, что луч RA. Возьмем какой-нибудь луч QQ, проходящий внутри угла BQR, обращенного своим отверстием в сторону параллельности, и докажем, что он пересекает луч RA. Для этого соединим какую-нибудь его точку Q c P; луч PQ пересечет RA в некоторой точке S ( так как прямая ВВ параллельна прямой АА в точке Р). Луч QQ, пересекающий сторону PS треугольника RPS, не может пересечь отрезка PR (так как тогда он проходил бы внутри смежного угла PQR) и не проходит ни через одну из вершин этого треугольника. Поэтому он должен пересечь отрезок PS. Таким образом, теорема доказана для того случая, когда точка Q расположена от точки Р в сторону параллельности.
Рассмотрим теперь тот случай, когда Q лежит в обратном направлении от точки Р. Соединим луч QQ, проходящий внутри угла BQR. Этот луч пересечет отрезок РR в некоторой точке S. Продолжая луч QQ по другую сторону точки Q, берем на этом продолжении точку Т. Прямая ТР проходит внутри угла RPB, т.е. пересекает RА в точке U. Итак, луч QQ пересекает сторону RP треугольника RPU, не пересекает отрезок PU и не проходит ни через одну из его вершин, т.е. пересекает отрезок RU. Таким образом, признак параллельности имеется в точке Q.
После того как доказана эта теорема, мы можем внести упрощение в терминологию теории параллельности: при указании. что прямая ВВ параллельна АА, не надо задавать той точки прямой ВВ, в которой имеется факт параллелизма.
4. Свойства функции П(х)
Задача 6. Доказать, что для каждого острого угла существует прямая, перпендикулярная к одной его стороне и параллельна другой.
Доказательство. Рассмотрим перпендикуляры, поставленные к стороне OQ острого угла POQ; среди них, конечно, найдутся такие, которые пересекают сторону ОР ( достаточно опустить из какой-нибудь точки луча ОР перпендикуляр на OQ). Покажем, что существует бесчисленное множество перпендикуляров, не пересекающих ОР.
Докажем это от противного, предполагая, что все перпендикуляры к стороне OQ пересекают ОР. Рассмотрим на луче OQ ряд точек А, А, А,…, Аn такой, что
АА =ОА, А А =ОА, А А =ОА, …, Аn-1An=OAn-1. Перпендикуляры, поставленные в точках А, А, …, Аn к стороне OQ, согласно предположению, пересекут луч ОР в точках В,В,В, …,Вn. Обозначая дефект треугольника ОАВ через D, имеем
DOAB=DOBA+DBAB=2DOAB+DBAB>2D,
DOA B =DOB A +DB A B =2DOA B +DB A B >22D,
.....................................................................,
DOanBn=DOBn-1An+DBn-1AnBn=2DOAn-1Bn-1+DBn-1AnBn >2nD.
Таким образом, увеличивая n, мы можем получить треугольник ОАnВn, у которого дефект превышает любое число, а это невозможно, так как дефект любого треугольника <2d.
Среди перпендикуляров к стороне OQ существуют не пересекающие сторону ОР. Рассмотрим один из них – MN. Если он параллелен ОР, теорема доказана. В противном случае разбиваем точки отрезка ОМ на два класса: к первому классу отнесем те точки, в которых перпендикуляры пересекают ОР, ко второму – те, в которых перпендикуляры не пересекают ОР. Ясно, что левее каждой точки первого класса лежат только точки первого же класса, т.е. классы лежат раздельно: второй класс лежит правее первого; таким образом, это – классы Дедекинда. Применяя аксиому Дедекинда, получаем точку D, разделяющие эти классы.
Покажем,что перпендикуляр DE к OQ параллелен ОР. Прежде всего этот перпендикуляр не может пересечь ОР, так как, если бы он пересекал ОР в точке F, то, опуская из точки G, лежащей на ОР правее F, перпендикуляр GJ на OQ, мы получили бы точку J первого класса, лежащую правее точки D. Остается показать, что любой луч DK, проходящий внутри угла ODE, пересекает ОР. Опуская из какой-нибудь точки К этого луча DK на OQ перпендикуляр KL, получим точку L первого класса, т.е. KL пересекает ОР в некоторой точке R. Прямая DK, пересекающая сторону LR треугольника ORL, должна пересечь отрезок OR.
Таким образом, перпендикуляр DE действительно параллелен ОР.
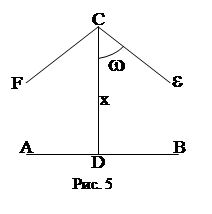
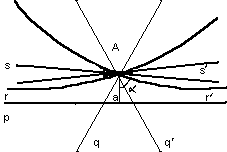
Задача 7. Доказать, что угол параллельности П(р) является убывающей функцией длины р перпендикуляра, принимающей все значения между 0 и d.
Доказательство. Пусть РР параллельна QQ, т.е. =П(РQ). Покажем, что эта функция убывающая.
В самом деле уменьшая ее аргумент, рассмотрим отрезок PR<PQ. Перпендикуляр RR к PQ пересекает РР, так как, проводя прямую QS, параллельную RR,мы получим треугольник PQT, одну из сторон которого пересекает RR, а так как RR параллельна QS она пересечет сторону РТ этого треугольника. Таким образом, П(PR)>П(PQ).
Заключение
Когда Евклид формулировал пятый постулат, вряд ли он знал, какую бурю тот вызовет. Когда Лобачевский отказался от пятого постулата, он не знал, что его «воображаемая геометрия» на проверку окажется реальной.
Нельзя сказать, что геометрия Лобачевского единственно правильна. На данный момент к ней нет никаких претензий. Но, может быть, через много лет она устареет.
Список использованной литературы
1. Верченко А.И., Научно-теоретический журнал. Москва, «Школа-Пресс» 1993г.
2. Ефимов Н.В., Высшая геометрия, «Наука», М.,1971г.
3. Лаптев Б.Л., Н.И.Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г.
4. Широков П.А., Краткий очерк основ геометрии Лобачевского. М. «Наука», 1983г.
5. Юшкевич А.П., История математики в России. М., «Наука», 1968г.
Приложения
Биография Лобачевского
Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря (20 ноября) 1792 года в Нижнем Новгороде, в России. Когда Николаю было 7 лет, его мать, Прасковья Ивановна, осталась одна с тремя маленькими сыновьями. И до этого жалование отца с трудом хватало на содержание семьи; теперь она встретилась с крайней нищетой. Она переехала в Казань, где как могла, подготавливала детей к школе, и они были приняты в гимназию на казенное содержание. Николай приступил к занятиям в 1802 году, в десятилетнем возрасте. Его успехи в математике и в древних языках были феноменальны. В 14 лет он был подготовлен для университета. В 1807 году он поступил в Казанский университет, в котором ему предстояло провести последующие 40 лет жизни – как студенту, экстраординарному профессору, профессору и, наконец, ректору.
В 1811 году, в возрасте 18 лет, Лобачевский получил степень магистра, к тому же с отличием. В это же время его старший брат Алексей вел курсы элементарной математики по подготовке младших правительственных чиновников, и, когда он получил отпуск по болезни, Николай заменил его. В апреле 1814 года он был утвержден адъюнктом чистой математики, а 2 года спустя ему было присвоено звание профессора.
Назначение Лобачевского экстраординарным профессором состоялось в 1816 году в необычно молодом возрасте 23 лет. Его обязанности были многотрудными. Дополнительно к работе по математике ему поручались лекционные курсы по астрономии и физике. Он блестяще справился с порученным заданием. Это послужило поводом для еще большей нагрузки.
Вскоре Лобачевский взялся за переустройство университетской библиотеки и университетского музея, находившихся в хаотическом состоянии.
Со смертью Александра I дела обернулись к лучшему. Специальный уполномоченный правительства для преднамеренного преследования Казанского был уволен. Нуждаясь в политической и моральной поддержке своей деятельности университете, новый попечитель обеспечил назначение в 1827 году Лобачевского ректором. Математик был теперь главой университета, но эта должность отнюдь не была синекурой. Под его умелым руководством весь штат был реорганизован, были привлечены лучшие люди, преподавание было либерализовано, не смотря на официальные препятствия, была построена библиотека, соответствующая высшему уровню научных требований, были организованы механические мастерские для изготовления научных инструментов, которые требовались для исследований и преподавания, была основана и оборудована обсерватория – любимое детище энергичного ректора.
Даже ректорское достоинство не удерживало Лобачевского от работы руками в библиотеке и музее, когда он чувствовал, что его помощь необходима. Университет был его жизнью, и он любил его.
Кажется невероятным, что Лобачевский, так сильно перегруженный преподавательскими и административными обязанностями, мог находить время для научной работы. Он создал один из величайших шедевров всей математики – неевклидову геометрию и поставил веху в человеческом мышлении. Он трудился над этим с перерывами не менее 20 лет. Его первое публичное сообщение по этой теме было сделано на физико-математическом факультете Казанского университета в 1826 году.
В 1846 году его грубо лишили должностей профессора и ректора университета, хотя тогда он был полон физических и умственных сил, более чем когда-либо он был способен продолжать свои математические исследования. Отвратительная неблагодарность властей сломила Лобачевского. Он оставил все надежды снова стать кем-то в университете, который своей научной славой почти целиком был обязан его усилиям, и после этого появлялся в нем только случайно, чтобы помочь на экзаменах. Хотя его зрение быстро ухудшалось, он был еще способен к интенсивному математическому мышлению.
Он все еще любил университет. Его здоровье пошатнулось, когда умер его сын; но он все еще надеялся, что сможет принести некоторую пользу. В 1855 году университет праздновал свое пятидесятилетие. Лобачевский лично присутствовал на торжествах и принес юбиляру экземпляр «Пангеометрии» - завершающей научной работы его жизни. Эта работа не была написана его собственной рукой: он диктовал ее, так как в то время был уже слепым. Через несколько месяцев, 24 февраля 1856 года, 62-х лет от роду, он умер
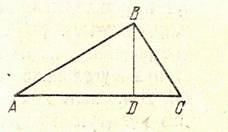
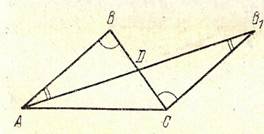
рис.
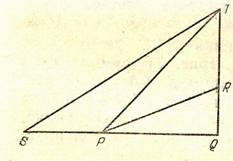
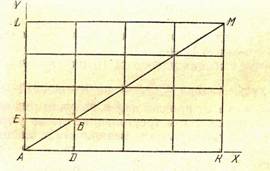
рис.
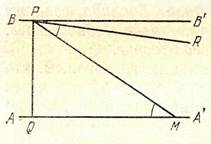
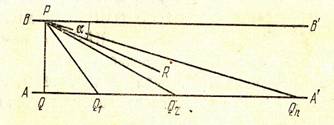
рис.
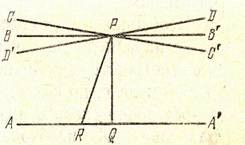
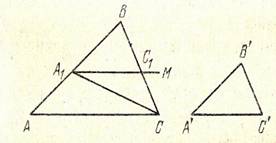
рис.
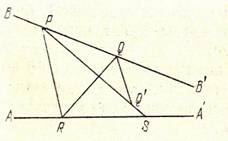
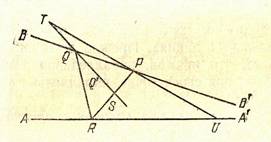
рис.
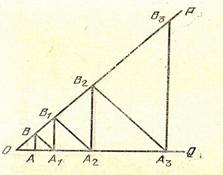
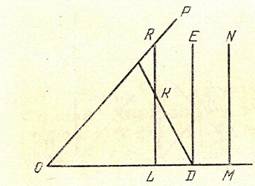
рис.
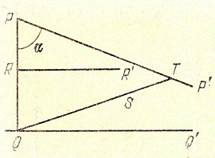
Рис.
Похожие работы
... 3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г. 4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г. Приложение 1 Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря(20 ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...
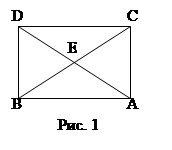

0 комментариев