Теорема Бернуллі про частоту ймовірності

4. Теорема Бернуллі про частоту ймовірності

Теорема. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність появи події дорівнює p, абсолютна величина відхилення відносної частоти появи події від імовірності появи події не перевищить позитивного числа , приблизно дорівнює подвоєної функції Лапласа при :

.

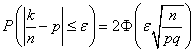Доказ. Будемо вважати, що виробляється n незалежних випробувань, у кожному з яких імовірність появи події А постійна й дорівнює p. Поставимо перед собою задачу знайти ймовірність того, що відхилення відносної частоти  від постійної ймовірності p по абсолютній величині не перевищує заданого числа . Інакше кажучи, знайдемо ймовірність здійснення нерівності

. (*)

Замінимо нерівність (*) йому рівносильними:

.

Множачи ці нерівності на позитивний множник , одержимо нерівності, рівносильні вихідному:

.

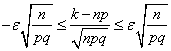Тоді ймовірність знайдемо в такий спосіб:

.

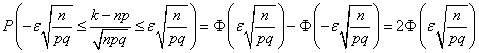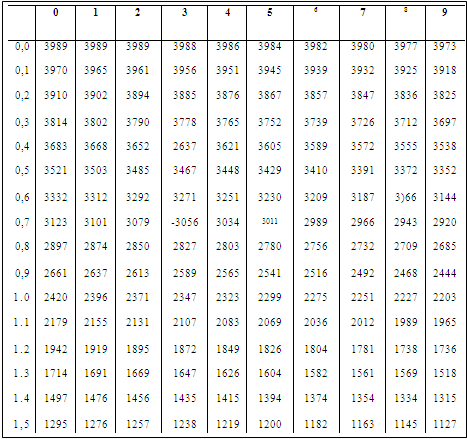
Значення функції  перебуває по таблиці(див. додаток 2).

Приклади

№20. Імовірність того, що деталь не стандартна, p=0,1. Знайти ймовірність того, що серед випадково відібраних 400 деталей відносна частота появи нестандартних деталей відхилиться від імовірності p=0,1 по абсолютній величині не більш, ніж на 0,03.

Рішення. n=400; p=0,1; q=0,9; =0,03. Потрібно знайти ймовірність . Користуючись формулою

,

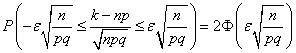маємо

.

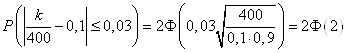По таблиці додатка 2 знаходимо . Отже, . Отже, шукана ймовірність дорівнює 0,9544.

№21. Імовірність того, що деталь не стандартна, p=0,1. Знайти, скільки деталей треба відібрати, щоб з імовірністю, рівної 0,9544, можна було затверджувати, що відносна частота появи нестандартних деталей(серед відібраних) відхилиться від постійної ймовірності p по абсолютній величині не більше ніж на 0,03.

Рішення. За умовою, p=0,1; q=0,9; =0,03; . Потрібно знайти n. Скористаємося формулою

.

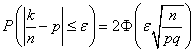У силу умови

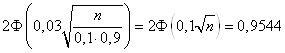
Отже,

По таблиці додатка 2 знаходимо . Для відшукання числа n одержуємо рівняння . Звідси шукане число деталей n=400.

№22. Імовірність появи події в кожному з незалежних випробувань дорівнює 0,2. Знайти, яке відхилення відносної частоти появи події від його ймовірності можна чекати з імовірністю 0,9128 при 5000 випробуваннях.

Рішення. Скористаємося тією же формулою, з якої треба:

.

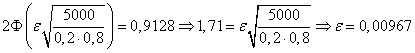Література

1. Гмурман Е.В. Теорія ймовірностей і математична статистика. – К., 2003

2. Гмурман Е.В. Керівництво до рішення задач по теорії ймовірностей і математичній статистиці. – К., 2004.

3. Гнеденко Б.В. Курс теорії ймовірностей. – К., 2007.

4. Колемаєв В.А., Калініна В.Н., Соловйов В.И., Малихин В.І., Курочкин О.П. Теорія ймовірностей у прикладах і задачах. – К., 2004.

5. Вентцель Е.С. Теорія ймовірностей. – К., 2004

Додатки

Додаток 1

Таблиця значень функції

	0	1	2	3	4	5	6	7	8	9
1.6	1109	1092	1074	1057	1040	1023	1006	0989	0973	0957
1.7	0940	0925	0909	0893	0878	0863	0648	0833	0818	0804
1.8	0790	0775	0761	0748	0734	0721	0707	0694	0681	0669
1.9	0656	0644	0632	0620	0608	0596	0584	0573	0562	0551
2,0	0540	0529	0519	0508	0498	0488	0478	0468	0459	0449
2.1	0440	0431	0422	0413	0404	0396	0387	0379	0371	0363
2.2	0355	0347	0339	0332	0325	0317	0310	0303	0297	0290
2.3	0283	0277	0270	0264	0258	0252	0246	0241	0235	0229
2,4	0224	0219	0213	0208	0203	0198	0194	0189	0184	0180
2.5	0175	0171	0167	0163	0158	0154	0151	0147	0143	0139
2.6	0136	0132	0129	0126	0122	0119	0116	0113	0110	0107
2,7	0104	0101	0099	0096	0093	0091	0088	0086	0084	0081
2,8	0079	0077	0075	0073	0071	0069	0067	0065	0063	0061
2.9	0060	0058	0056	0055	0053	0051	0050	0048	0047	0043
3,0	0044	0043	0042	0040	0039	0038	0037	0036	0035	0034
3,1	0033	0032	0031	0030	0029	0028.	0027	0026	0025	0025
3,2	0024	0023	0622	0022	0021	0020	0020	0019	0018	0018
3,3	0017	0017	0016	0016	0015	0015	0014	0014	0013	0013
3,4	0012	0012	0012	0011	0011	0010	0010	0010	0009	0009
3,5	0009	0008	0008	0008	0008	0007	0007	0007	0007	0006
3,6	0006	0006	0006	0005	0005	0005	0005	0005	0005	0004
3,7	0004	0004	0004	0004	0004	0004	0003	0003	0003	0003
3,8	0003	0003	0003	0003	0003	0002	0002	0002	0002	0002
3,9	0002	0002	0002	0002	0002	0002	0002	0002	0001	0001

Додаток 2

Таблиця значень функції

x		x		x		x
0900	0,0000	0,32	0,1255	0,64	0,2389	0,96	0,3315
0,01	0,0040	0,33	0,1293	0,65	0,2422	0,97	0,3340
0,02	0,0080	0,34	0,1331	0,66	0,2454	0,98	0,3365
0,03	0,0120	0,35	0,1368	0,67	0,2486	0.99	0,3389
0,04	0,0160	0,36	0,1406	0,68	0,2517	1,00	0,3413
0,05	0,0199	0,37	0,1443	0,69	0,2549	1,01	0,3438
0,06	0,0239	0,38	0,1480	0,70	0,2580	1,02	0,3461
0,07	0,0279	0,39	0,1517	0,71	0,2611	1,03	0,3485
0,08	0,0319	0,40	0,1554	0,72	0,2642	1,04	0,3508
0,09	0,0359	0,41	0,1591	0,73	0,2673	1,05	0,3531
0,10	0,0398	0,42	0,1628	0,74	0,2703	1,06	0,3554
0,11	0,0438	0,43	0,1664	0,75	0,2734	1,07	0,3577
0,12	0,0478	0,44	0,1700	0,76	0,2764	1,08	0,3599
0,13	0,0517	0,45	0,1736	0,77	0,2794	1.09	0,3621
0,14	0,0557	0,46	0,1772	0,78	0,2823	1.10	0,3643
0,15	0,0596	0,47	0,1808	0,79	0,2852	3665	0,3665
0,16	0,0636	0,48	0,1844	0,80	0,2881	3686	0,3686
0,17	0,0675	0,49	01879	0,81	0,2910	1,13	0,3708.
0,18	0,0714	0,50	0,1915	0,82	0,2939	1,14	0,3729
0,19	0,0753	0,51	0,1950	0,83	0,2967	1,15	0,3749
0,20	0,0793	0,52	0,1985	0,84	0,2995	1,16	0,3770
0,21	0,0832	0,53	0,2019	0,85	0,3023	1,17	0,3790
0,22	0,0871	0,54	0,2054	0,86	0,3051	1,18	0,3810
0,23	0,0910	0,55	0,2088	0,87	0,3078	1,19	0,3830
0,24	0,0948	0,56	0,2123	0,88	0,3106	1,20	0,3849
0,25	0,0987	0,57	0,2157	0,89	0,3133	1.21	0,3869
0,26	0,1026	0,58	0,2190	0,90	0,3159	1,22	0/3883
0,27	0,1064	0,59	0,2224	0,91	0,3186	1,23	0,3907
0,28	0,1103	0,60	0,2257	0,92	0,3212	1.24	0,3925
0,29	0,1141	0,61	0,2291	0,93	0,3238	1,25	0,3944
0,30	0,1179	0,62	0,2324	0,94	0,3264
0,31	0,1217	0,63	0,2357	0,95	0,3289

x		x		x		x
1,26	0,3962	1,59	0,4441	1,92	0,4726	2,50	0,4938
1,27	0,3980	1,60	0,4452	1,93	0,4732	2,52	0,4941
1,28	0,3997	1,61	0,4463	1,94	0,4738	2,54	0,4945
1,29	0.4015	1,62	0,4474	1,95	0,4744	2,56	0,4948
1,30	0,4032	1,63	0.4484	1.96	0,4750	2,58	0,4951
1,31	0,4049	1,64	0,4495	1,97	0,4756	2,60	0,4953
1,32	0.4066	1,65	0,4505	1,98	0,4761	2,62	0,4956
1,33	0,4082	1,66	0,4515	1,99	0,4767	2,64	0,4959
1,34	0.4099	1,67	0.4525	2.00	0,4772	2,66	0,4961
1.3S	0.4115	1,68	0,4535	2,02	0,4783	2,68	0,4963
1,36	0.4131	1,69	0,4545	2,04	0,4793	2,70	0,4965
1,37	0.4147	1,70	0,4554	2,06	0,4803	2,72	0,4967
1,38	0.4162	1.71	0,4564	2,08	0,4812	2,74	0,4969
1,39	0.4177	1,72	0,4573	2,10	0,4821	2,76	0,4971
1.40	0,4192	1,73	0,4582	2,12	0,4830	2,78	0,4973
1.41	0,4207	1.74	0,4591	2,14	0,4838	2,80	0,4974
1.42	0.4222	1,75	0.4599	2,16	0,4846	2,82	0,4976
1.43	0.4236	1,76	0,4608	2,18	0,4854	2,84	0,4977
1.44	0,4251	1.77	0,4616	2,20	0,4861	2,86	0,4979
1,45	0.4265	1,78	0.4625	2,22	0,4868	2,88	0,4980
1.46	0,4279	1,79	0,4633	2,24	0,4875	2,90	0,4981
1.47	0,4292	1,80	0,4641	2,26	0,4881	2,92	0,4982
1,48	0,4306	1.81	0,4649	2,28	0,4887	2,94	0,4984
1,49	0.4319	1,82	0,4656	2,30	0,4893	2,96	0,4985
1.50	0,4332	1,83	0,4664	2,32	0,4898	2.98	0,4986
1,51	0,4345	1,84	0,4671	2,34	0,4904	3,00	0,49865
1.52	0,4357	1,85	0,4678	2,36	0,4909	3,20	0,49931
1.53	0,4370	1,86	0,4686	2,38	0,4913	3.40	0,49966
1.54	0,4382	1,87	0,4693	2,40	0,4918	3,60	0,49984
1,55	0,4394	1.88	0,4699	2,42	0,4922	3,80	0,49992
1.S6	0,4406	1.89	0,4706	2,44	0,4927	4,00	0,49996
1,57	0,4418	1,90	0,4713	2,46	0,4931	4,50	0,49999
1,58	0,4429	1,91	0,4719	2,48	0,4934	5,00	0,49999