Навигация
Применение балансового метода в изучении основных фондов
3. Применение балансового метода в изучении основных фондов
3.1 Статистические методы, используемые в изучении ОФ
Основными методами являются сводка и группировка, обобщающие статистические показатели (выраженные абсолютными, относительными и средними величинами), статистические методы анализа рядов динамики, индексный, балансовый, табличный, графический и др.
Балансовый метод
Наиболее полное представление об изменении объема основных фондов за год можно получить на основе балансового метода. Данный метод используется для получения характеристики воспроизводства основных фондов. Для этой цели составляется баланс основных фондов.
Баланс основных фондов - представляет собой статистическую таблицу, данные которой характеризуют объем, структуру, воспроизводство основных фондов по экономике в целом, отраслям и формам собственности. По данным этого баланса исчисляются показатели износа, годности, обновления, выбытия, использования основных фондов. Данные о наличии основных фондов используются для расчета показателей фондоемкости, фондовооруженности, фондоотдачи и др. расчетов. Балансы основных фондов составляются в двух видах - по полной первоначальной балансовой стоимости и по остаточной балансовой стоимости, что может быть выражено в текущих ценах, среднегодовых ценах и в постоянных ценах базисного периода.
Баланс основных фондов по полной балансовой стоимости отражает изменение объема основных фондов без учета их физического состояния. Взаимосвязь между показателями баланса выражается в последнем показателе, который есть сумма стоимостей основных фондов на начало года и стоимостей основных фондов, поступивших в течение отчетного года из разных источников за вычетом стоимости выбывших основных фондов в течение отчетного года по всем направлениям выбытия.
Таблица 2
Баланс основных фондов по балансовой стоимости, млн. руб.
| Виды основных фондов в группировке по разным признакам | Наличие на начало года | Поступило в отчетном году | Выбыло в отчетном году | Наличие на конец года | ||||
| Всего | В том числе | Всего | В том числе | |||||
| ввод в действие | прочие поступления | выбытие по ветхости и износу | прочее выбытие | |||||
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 = 1 + 3 + 4 – 6 – 7 |
В отличие от баланса основных фондов по полной стоимости, который призван отражать процесс воспроизводства основных фондов в их физическом объеме, баланс основных фондов по остаточной балансовой стоимости характеризует изменение реальной стоимости не только по вводу и выбытию основных фондов, но и с учетом частичного восстановления их стоимости путем капитального ремонта и амортизации.
Таблица 3
Баланс основных фондов по остаточной стоимости, млн. руб.
| Виды ОФ в группировке по разным признакам | Наличие ОФ на начало года | В течение года | Наличие ОФ на конец года | |||
| ввод в действие ОФ | произведенный капитальный ремонт | выбытие по ветхости | амортизация | |||
| А | 1 | 2 | 3 | 4 | 5 | 6 = 1+2+3–4–5 |
Оценка Основных фондов по балансовой стоимости учитывает их в момент постановки на учет в бухгалтерском балансе. Балансовая стоимость представляет собой, таким образом, смешанную оценку основных фондов, т.к. часть инвентарных объектов числится на балансах по восстановительной стоимости на момент последней переоценки, а основные фонды, введенные в последующий период, учитываются по первоначальной стоимости (стоимости приобретения).
Среднегодовая стоимость Основных фондов - среднее значение показателя наличия основных фондов в течение года. Среднегодовые основные фонды исчисляются по формуле средней хронологической как частное от деления на 12 суммы, полученной от сложения половины стоимости всех основных фондов на начало и конец отчетного года и стоимости основных фондов на первое число всех остальных месяцев отчетного года.
Таким образом, балансовый метод применяется для анализа связей и пропорций изучаемых явлений. Он позволяет связать в единую систему абсолютные уровни, характеризующие движение ресурсов (материальных, трудовых, финансовых). Показатели в таких балансах образуют начальный и конечный остатки, поступление и расход, т.е. следующее балансовое равенство: остаток на начало периода + поступление за период = расход за период + остаток на конец периода
Балансы применяются для анализа взаимосвязей и пропорций как в пределах 1-го или совокупности предприятий, так и для отрасли, экономического района и экономики в целом. Поэтому, такие балансы позволяют выявлять складывающиеся пропорции в движении ресурсов между отдельными предприятиями, районами, отраслями экономики, изучать межотраслевую и межрегиональную связь.
Расчетная часть
Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности региона в отчетном году (выборка 20%-ная механическая), млн. руб.:
Таблица 1
| № предприятия п/п | Выпуск продукции | Среднегодовая стоимость основных производственных фондов | № предприятия п/п | Выпуск продукции | Среднегодовая стоимость основных производственных фондов |
| 1 | 36,450 | 34,714 | 16 | 36,936 | 34,845 |
| 2 | 23,400 | 24,375 | 17 | 53,392 | 46,428 |
| 3 | 46,540 | 41,554 | 18 | 41,000 | 38,318 |
| 4 | 59,752 | 50,212 | 19 | 55,680 | 47,590 |
| 5 | 41,415 | 38,347 | 20 | 18,200 | 19,362 |
| 6 | 26,860 | 27,408 | 21 | 31,800 | 31,176 |
| 7 | 79,200 | 60,923 | 22 | 39,204 | 36,985 |
| 8 | 54,720 | 47,172 | 23 | 57,128 | 48,414 |
| 9 | 40,424 | 37,957 | 24 | 28,440 | 28,727 |
| 10 | 30,210 | 30,210 | 25 | 43,344 | 39,404 |
| 11 | 42,418 | 38,562 | 26 | 70,720 | 55,250 |
| 12 | 64,575 | 52,500 | 27 | 41,832 | 38,378 |
| 13 | 51,612 | 45,674 | 28 | 69,345 | 55,476 |
| 14 | 35,420 | 34,388 | 29 | 35,903 | 34,522 |
| 15 | 14,400 | 16,000 | 30 | 50,220 | 44,839 |
Задание 1.
По исходным данным:
1. Постройте статистический ряд распределения предприятий по признаку эффективность использования основных производственных фондов – фондоотдача, образовав пять групп с равными интервалами.
2. Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану
Сделайте выводы по результатам выполнения задания.
Задание 2
По исходным данным:
1. Установите наличие и характер связи между признаками – эффективность использования основных производственных фондов (фондоотдача) и выпуск продукции методом аналитической группировки, образовав пять групп с равными интервалами по факторному признаку.
2. Измерьте тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения.
Сделайте выводы по результатам выполнения задания.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,683 определите:
1. Ошибку выборки среднего уровня фондоотдачи и границы, в которых он будет находиться в генеральной совокупности.
2. Ошибку выборки доли организаций с уровнем фондоотдачи 1,14 руб. и более и границы, в которых будет находиться генеральная доля.
Задание 4.
Имеются следующие данные о наличии и движении основных производственных фондов организаций за год, млн. руб.:
Полная первоначальна стоимость на начало года....................... 50,2
В течение года:
- введено новых................................................................................. 7,8
- выбыло по стоимости за вычетом износа.................................... 0,45
- полная стоимость выбывших фондов............................................ 4,8
Износ основных фондов на начало года, %..................................... 20
Годовая норма амортизации, %....................................................... 10
По приведенным данным:
1. Постройте баланс основных производственных фондов по полной стоимости; по данным этого баланса рассчитайте показатели движения основных фондов.
2. Постройте баланс основных фондов по остаточной стоимости; по данным этого баланса рассчитайте коэффициенты состояния основных производственных фондов на начало и конец года.
Сделайте выводы.
Задание 1
Решение:
1.1 Для построения ряда распределения необходимо определить признак - инвестиции в основные фонды (таблица 1).
Таблица 1
| № предприятия п/п | Выпуск продукции | Среднегодовая стоимость основных производственных фондов | Фондоотдача | № предприятия п/п | Выпуск продукции | Среднегодовая стоимость основных производственных фондов | Фондоотдача |
| 1 | 36,450 | 34,714 | 1,050 | 16 | 36,936 | 34,845 | 1,060 |
| 2 | 23,400 | 24,375 | 0,960 | 17 | 53,392 | 46,428 | 1,150 |
| 3 | 46,540 | 41,554 | 1,120 | 18 | 41,000 | 38,318 | 1,070 |
| 4 | 59,752 | 50,212 | 1,190 | 19 | 55,680 | 47,590 | 1,170 |
| 5 | 41,415 | 38,347 | 1,080 | 20 | 18,200 | 19,362 | 0,940 |
| 6 | 26,860 | 27,408 | 0,980 | 21 | 31,800 | 31,176 | 1,020 |
| 7 | 79,200 | 60,923 | 1,300 | 22 | 39,204 | 36,985 | 1,060 |
| 8 | 54,720 | 47,172 | 1,160 | 23 | 57,128 | 48,414 | 1,180 |
| 9 | 40,424 | 37,957 | 1,065 | 24 | 28,440 | 28,727 | 0,990 |
| 10 | 30,210 | 30,210 | 1,000 | 25 | 43,344 | 39,404 | 1,100 |
| 11 | 42,418 | 38,562 | 1,100 | 26 | 70,720 | 55,250 | 1,280 |
| 12 | 64,575 | 52,500 | 1,230 | 27 | 41,832 | 38,378 | 1,090 |
| 13 | 51,612 | 45,674 | 1,130 | 28 | 69,345 | 55,476 | 1,250 |
| 14 | 35,420 | 34,388 | 1,030 | 29 | 35,903 | 34,522 | 1,040 |
| 15 | 14,400 | 16,000 | 0,900 | 30 | 50,220 | 44,839 | 1,120 |
Чтобы построить статистический ряд распределения организации, образовав пять групп с равными интервалами, определим величину интервала:
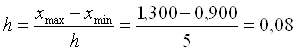 (руб.)
(руб.)
Отсортированные данные
Таблица 2
| № предприятия п/п | Выпуск продукции | Среднегодовая стоимость основных производственных фондов | Фондоотдача |
| 15 | 14,400 | 16,000 | 0,900 |
| 20 | 18,200 | 19,362 | 0,940 |
| 2 | 23,400 | 24,375 | 0,960 |
| Всего | 56,000 | 59,737 | 2,800 |
| 6 | 26,860 | 27,408 | 0,980 |
| 24 | 28,440 | 28,727 | 0,990 |
| 10 | 30,210 | 30,210 | 1,000 |
| 21 | 31,800 | 31,176 | 1,020 |
| 14 | 35,420 | 34,388 | 1,030 |
| 29 | 35,903 | 34,522 | 1,040 |
| 1 | 36,450 | 34,714 | 1,050 |
| Всего | 225,083 | 221,145 | 7,110 |
| 22 | 39,204 | 36,985 | 1,060 |
| 16 | 36,936 | 34,845 | 1,060 |
| 9 | 40,424 | 37,957 | 1,065 |
| 18 | 41,000 | 38,318 | 1,070 |
| 5 | 41,415 | 38,347 | 1,080 |
| 27 | 41,832 | 38,378 | 1,090 |
| 25 | 43,344 | 39,404 | 1,100 |
| 11 | 42,418 | 38,562 | 1,100 |
| 3 | 46,540 | 41,554 | 1,120 |
| 30 | 50,220 | 44,839 | 1,120 |
| 13 | 51,612 | 45,674 | 1,130 |
| Всего | 474,954 | 434,863 | 11,995 |
| 17 | 53,392 | 46,428 | 1,150 |
| 8 | 54,720 | 47,172 | 1,160 |
| 19 | 55,680 | 47,590 | 1,170 |
| 23 | 57,128 | 48,414 | 1,180 |
| 4 | 59,752 | 50,212 | 1,190 |
| Всего | 280,672 | 239,816 | 5,850 |
| 12 | 64,575 | 52,500 | 1,230 |
| 28 | 69,345 | 55,476 | 1,250 |
| 26 | 70,720 | 55,250 | 1,280 |
| 7 | 79,200 | 60,923 | 1,300 |
| Всего | 283,840 | 224,149 | 5,060 |
Таким образом, имеем следующее распределение предприятий по группам (таблица 3):
Распределение предприятий по группам
Таблица 3
| № п/п | Группа пред-тий по величине фондоотдачи | Число пред-тий | Сумма наблюдений | |
| 1 | 0,900 – 0,980 | 3 | 3 | |
| 2 | 0,980 – 1,060 | 7 | 10 | |
| 3 | 1,060 – 1,140 | 11 | 21 | |
| 4 | 1,140 – 1,220 | 5 | 26 | |
| 5 | 1,220 – 1,300 | 4 | 30 | |
| Итого | 30 |
1.2 Строим график:
Гистограмма
![]()
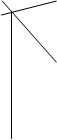
Вычисляем моду по формуле:

где хМo – нижняя граница модального интервала,
h –величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 – частота интервала, следующего за модальным.
![]()
Таким образом, у данной совокупности предприятий фондоотдача, характеризуется средней величиной 1,092 млн.руб.
0,9-0,98 – 3 предприятия
098-1,06 – 7 предприятий
1,06-1,14 – 11 предприятий
1,14-1,22 – 5 предприятий
1,22-1,30 – 4 предприятия
Строим график по накопительным частотам (кумулятам):
![]()
![]()
![]()
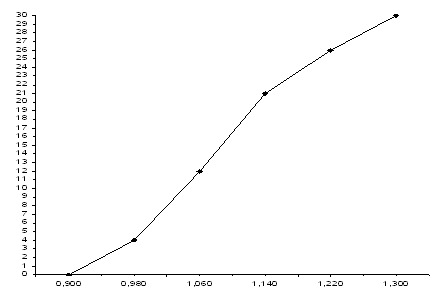
По кумуляте нашли медиану (это значение признака у центральной единицы совокупности).
Медиана рассчитывается по формуле:
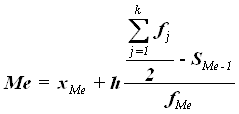
где хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
![]() – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.
Определяем медианный интервал, в котором находится порядковый номер медианы (n).
![]() он находится в интервале 1,060 – 1,140.
он находится в интервале 1,060 – 1,140.
![]() (руб.)
(руб.)
Таким образом, половина предприятий имеет фондоотдачу не больше 1,096 млн.руб., а другая половина – не меньше 1,096млн.руб.
Вычисляем среднее значение и показателей вариации в интервальном вариационном ряду.
Чтобы рассчитать характеристики ряда распределения: среднеарифметическую, среднее квадратическое отклонение, коэффициент вариации, рассчитаем необходимые расчетные значения и результаты представим в таблице 4:
Таблица 4
| Группа пред-тий по величине фондоотдачи | Число пред-тий fj | Середина интервала | Расчетное значение | |||
|
|
|
|
| |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0,900 – 0,980 | 3 | 0,940 | 2,82 | -0,160 | 0,026 | 0,077 |
| 0,980 – 1,060 | 7 | 1,020 | 7,14 | -0,080 | 0,006 | 0,045 |
| 1,060 – 1,140 | 11 | 1,100 | 12,1 | 0,000 | 0,000 | 0,000 |
| 1,140 – 1,220 | 5 | 1,180 | 5,9 | 0,080 | 0,006 | 0,032 |
| 1,220 – 1,300 | 4 | 1,260 | 5,1 | 0,160 | 0,026 | 0,102 |
| Итого | 30 | 33,00 | 0,256 | |||
Таблица с необходимыми расчетными значениями для расчета характеристик ряда распределения.
Средняя арифметическая определяется по формуле:
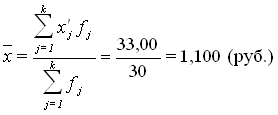
Средне квадратическое отклонение:
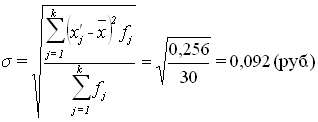
Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
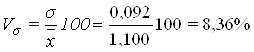
Вывод:
В результате группировки образовалось пять групп с равными интервалами равными 0,08, где выяснилось, что наиболее многочисленной является третья группа предприятий у которых величина фондоотдачи от 1,060 – 1,140 руб., в эту группу входят 11 предприятий. Второй по численности является вторая группа предприятий, куда входят 7 предприятий, и величина фондоотдачи от 0,980 – 1,060 . Третьей группой по численности является четвертая группа, куда входят 5 предприятий, величина фондоотдачи от 1,140 – 1,220. Четвертой по численности является пятая группа величина фондоотдачи которых от 1,220 – 1,300. Пятой по численности является первая группа, куда входит 3 предприятия, величина фондоотдачи от 0,9-0,98.
Средняя фондоотдача для этой совокупности составляет 1,092. Наиболее часто встречаются предприятия с фондоотдачей около 1,096. У 50% предприятий фондоотдача более 1,096, а у первой и второй группы предприятий фондоотдача менее 1,096. В среднем разница между фондоотдачей у какого – либо из предприятий от их среднего значения составляет 0,0976.
В среднем фондоотдача отклоняется от средних значений на 0,001 млн.руб. Данная совокупность является количественно однородной, т.к. коэффициент вариации равен 8,36, а значит не превышает нормальное состояние 33%. Значит, найденное среднее значение объема фондоотдачи (1,1) является типично, надежной характеристикой исследуемой совокупности предприятий.
Задание 2
Решение:
2.1 При использовании метода аналитической группировки строится интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение ![]() результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения ![]() систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Строим аналитическую группировку, характеризующую зависимость между факторным признаком Х – Выпуск продукции и результативным признаком Y – Фондоотдача. Групповые средние значения ![]() получаем из таблицы 2, основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 5.
получаем из таблицы 2, основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 5.
Таблица 5
| Номер группы | Группы предприятий по фондоотдаче, руб.,х | Число предприятий, fj | Сумма выпуска продукции, млн. руб. | |
| всего | в среднем на одно предприятие,
| |||
| 1 | 2 | 3 | 4 | 5=4:3 |
| 1 | 0,900 – 0,980 | 3 | 56,000 | 18,667 |
| 2 | 0,980 – 1,060 | 7 | 225,083 | 32,155 |
| 3 | 1,060 – 1,140 | 11 | 474,945 | 43,177 |
| 4 | 1,140 – 1,220 | 5 | 280,672 | 56,134 |
| 5 | 1,220 – 1,300 | 4 | 283,840 | 70,960 |
| Итого | 30 | 1320, 540 | 221,093 | |
Вывод. Данные таблицы 6 показывают, что с ростом инвестиций в основные фонды нераспределенная прибыль увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная связь.
2.2 Теперь определяем тесноту связи:
Для ее измерения между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации ![]() и эмпирическое корреляционное отношение
и эмпирическое корреляционное отношение ![]() .
.
Эмпирический коэффициент детерминации ![]() оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель
оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель ![]() рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
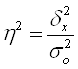 ,
,
где ![]() – общая дисперсия признака Y,
– общая дисперсия признака Y,
![]() – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Значения показателя ![]() изменяются в пределах
изменяются в пределах ![]() . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи между признаками Х и Y имеет место равенство ![]() =0, а при наличии функциональной связи между ними - равенство
=0, а при наличии функциональной связи между ними - равенство![]() =1.
=1.
Общая дисперсия ![]() характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
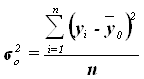 ,
,
где yi – индивидуальные значения результативного признака;
![]() – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя ![]() как средняя взвешенная по частоте групп интервального ряда:
как средняя взвешенная по частоте групп интервального ряда:
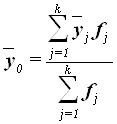
Расчет ![]()

Для расчета общей дисперсии ![]() применяется вспомогательная таблица 6.
применяется вспомогательная таблица 6.
Таблица 6
| Номер пред-тий п/п | Выпуск продукции, млн руб. |
|
|
|
| 1 | 2 | 3 | 4 | 5 |
| 1 | 36,45 | -7,568 | 57,275 | 1328,603 |
| 2 | 23,4 | -20,618 | 425,102 | 547,560 |
| 3 | 46,54 | 2,522 | 6,360 | 2165,972 |
| 4 | 59,752 | 15,734 | 247,559 | 3570,302 |
| 5 | 41,415 | -2,603 | 6,776 | 1715,202 |
| 6 | 26,86 | -17,158 | 294,397 | 721,460 |
| 7 | 79,2 | 35,182 | 1237,773 | 6272,640 |
| 8 | 54,72 | 10,702 | 114,533 | 2994,278 |
| 9 | 40,424 | -3,594 | 12,917 | 1634,100 |
| 10 | 30,21 | -13,808 | 190,661 | 912,644 |
| 11 | 42,418 | -1,600 | 2,560 | 1799,287 |
| 12 | 64,575 | 20,557 | 422,590 | 4169,931 |
| 13 | 51,612 | 7,594 | 57,669 | 2663,799 |
| 14 | 35,42 | -8,598 | 73,926 | 1254,576 |
| 15 | 14,4 | -29,618 | 877,226 | 207,360 |
| 16 | 36,936 | -7,082 | 50,155 | 1364,268 |
| 17 | 53,392 | 9,374 | 87,872 | 2850,706 |
| 18 | 41 | -3,018 | 9,108 | 1681,000 |
| 19 | 55,68 | 11,662 | 136,002 | 3100,262 |
| 20 | 18,2 | -25,818 | 666,569 | 331,240 |
| 21 | 31,8 | -12,218 | 149,280 | 1011,240 |
| 22 | 39,204 | -4,814 | 23,175 | 1536,954 |
| 23 | 57,128 | 13,110 | 171,872 | 3263,608 |
| 24 | 28,44 | -15,578 | 242,674 | 808,834 |
| 25 | 43,344 | -0,674 | 0,454 | 1878,702 |
| 26 | 70,72 | 26,702 | 712,997 | 5001,318 |
| 27 | 41,832 | -2,186 | 4,779 | 1749,916 |
| 28 | 69,345 | 25,327 | 641,457 | 4808,729 |
| 29 | 35,903 | -8,115 | 65,853 | 1289,025 |
| 30 | 50,22 | 6,202 | 38,465 | 2522,048 |
| Итого | 1320,54 | 0,000 | 7028,034 | 65155,564 |
Расчет общей дисперсии:
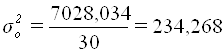
Межгрупповая дисперсия ![]() измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних ![]() от общей средней
от общей средней ![]() . Показатель
. Показатель ![]() вычисляется по формуле
вычисляется по формуле
 ,
,
где ![]() –групповые средние,
–групповые средние,
![]() – общая средняя,
– общая средняя,
![]() –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета межгрупповой дисперсии ![]() строится вспомогательная таблица 7:
строится вспомогательная таблица 7:
Таблица 7
| Группы пред-тий по фондоотдаче, млн руб. | Число преприятий,
| Среднее значение |
|
|
| 1 | 2 | 3 | 4 | 5 |
| 0,900 – 0,980 | 3 | 18,667 | -25,351 | 1928,070 |
| 0,980 – 1,060 | 7 | 32,155 | -11,863 | 985,163 |
| 1,060 – 1,140 | 11 | 43,177 | -0,841 | 7,783 |
| 1,140 – 1,220 | 5 | 56,134 | 12,116 | 734,036 |
| 1,220 – 1,300 | 4 | 70,960 | 26,942 | 2903,485 |
| Итого | 30 | 6558,538 |
Расчет межгрупповой дисперсии ![]() :
:
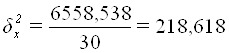
Расчет эмпирического коэффициента детерминации ![]() по формуле:
по формуле:
 или 93,3%
или 93,3%
Вывод. 93,3% вариации суммы фондоотдачи предприятия обусловлено вариацией выпуска продукции, а 6,7% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение ![]() оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

Значение показателя изменяются в пределах ![]() . Чем ближе значение
. Чем ближе значение ![]() к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе ![]() служит шкала Чэддока (табл. 8):
служит шкала Чэддока (табл. 8):
Таблица 8
| h | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характ-ка силы связи | Слабая | Умеренная | Заметная | Тесная | Весьма тесная |
Расчет эмпирического корреляционного отношения ![]() по формуле:
по формуле:
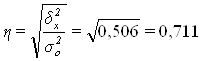 или 71,1%
или 71,1%
Вывод. Согласно шкале Чэддока связь между выпуском продукции и суммой фондоотдачи предприятия является тесной.
Задание 3
Решение:
3.1 Применение выборочного метода наблюдения всегда связано с установлением степени достоверности оценок показателей генеральной совокупности, полученных на основе значений показателей выборочной совокупности. Достоверность этих оценок зависит от репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности. Как правило, генеральные и выборочные характеристики не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки (ошибкой репрезентативности).
Значения признаков единиц, отобранных из генеральной совокупности в выборочную, всегда случайны, поэтому и статистические характеристики выборки случайны, следовательно, и ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок - среднюю ![]() и предельную
и предельную ![]() .
.
Средняя ошибка выборки ![]() - это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания M[
- это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания M[![]() ].
].
Величина средней ошибки выборки рассчитывается дифференцированно (по различным формулам) в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.
Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка ![]() выборочной средней
выборочной средней ![]() определяется по формуле
определяется по формуле
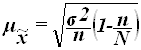
где ![]() – общая дисперсия выборочных значений признаков,
– общая дисперсия выборочных значений признаков,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки ![]() определяет границы, в пределах которых будет находиться генеральная средняя:
определяет границы, в пределах которых будет находиться генеральная средняя:
![]() ,
,
![]()
где ![]() – выборочная средняя,
– выборочная средняя,
![]() – генеральная средняя.
– генеральная средняя.
Границы задают доверительный интервал генеральной средней, т.е. случайную область значений, которая с вероятностью Р гарантированно содержит значение генеральной средней. Эту вероятность Р называют доверительной вероятностью или уровнем надёжности.
Для предельной ошибки выборочной средней ![]() выражается формулой
выражается формулой
![]()
По условию выборочная совокупность насчитывает 30 банков, выборка 20% механическая, следовательно, генеральная совокупность включает 150 предприятий (30/0,2) Выборочная средняя ![]() , дисперсия
, дисперсия ![]() определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 9:
определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 9:
Таблица 9
Р | t | n | N |
|
|
| 0,683 | 1,0 | 30 | 150 | 1,100 | 0,0085 |
1) Расчет генеральной совокупности
Расчет средней ошибки выборки:
 ,
,
Расчет предельной ошибки выборки:
![]()
Определение по формуле (16) доверительного интервала для генеральной средней:
1,1-0,015![]() 1,1+0,015,
1,1+0,015,
1,085 руб. ![]() 1,115 руб.
1,115 руб.
Вывод. На основании проведенного выборочного обследования предприятий региона с вероятностью 0,683 можно утверждать, что для генеральной совокупности предприятий средняя фондоотдача предприятий находится в пределах от 1,085 руб. до 1,115 руб.
Похожие работы
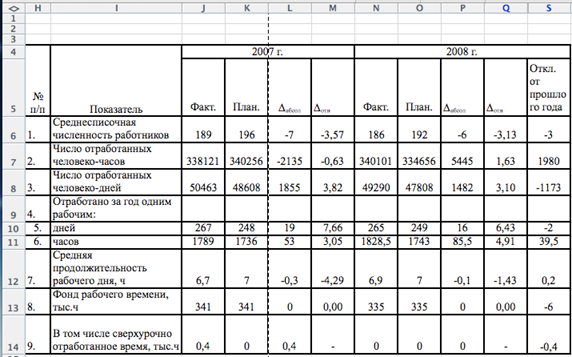
... выработка и т.д. В стоимостном выражении выработка может быть представлена: w = , где: ВП – валовая продукция за месяц, квартал и т.д.; - среднесписочная численность. 1.3 Применение балансового метода в изучении трудовых показателей Для полноты картины о фондах времени и их использовании рекомендуется применять балансы рабочего времени. При этом особенно наглядными балансы ...
... нематериальных активов в учете и отчетности. Причина этого заключается как в объективной сложности самого понятия нематериальных активов, так и в отсутствии длительного опыта их отражения в российском учете. Поэтому предпринимаются попытки оценки общей стоимости нематериальных основных фондов на макроэкономическом уровне на основе данных о затратах на науку в части, образующей стоимость ...
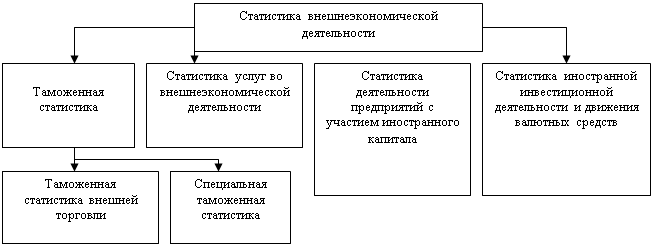
... . При расширении производства экспортной продукции, реализуемой данной страной на мировом рынке, коэффициент диверсификации приближается к 0. [15] 2. статистическое изучение внешнеэкономических связей россии Рассмотрим внешнеэкономическую деятельность Российской Федерации на примере внешнеэкономических контрактов Забайкальской железной дороги. 2.1 Понятие забайкальской железной дороги, её ...
... оцениваемого объекта определяется текущей стоимостью доходов, которые этот объект может принести своему собственнику. 2. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СОСТАВА, СТРУКТУРЫ И СОСТОЯНИЯ ОСНОВНЫХ ФОНДОВ. 2.1. Состав и структура основных фондов предприятия, анализ динамики. ОСНОВНЫЕ ФОНДЫ ПРЕДПРИЯТИЯ представляют ...


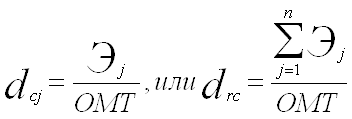
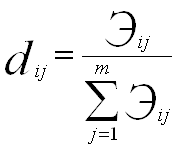

0 комментариев