Навигация
РАСЧЕТ ОСНОВНЫХ ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯДА
4. РАСЧЕТ ОСНОВНЫХ ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯДА
4.1 РАСЧЕТ СРЕДНИХ ВЕЛИЧИННаиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.
Средняя арифметическая простая испоьзуется в тех случаях, когда расчет осуществляется по несгруппированным данным (3.5).
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по нескольку раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.
Средняя арифметическая взвешенная вычисляется по формуле:
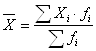 , (5.1)
, (5.1)
где ![]() – среднее значение;
– среднее значение;
![]() – i-ый член совокупности;
– i-ый член совокупности;
![]() - частота.
- частота.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.
Рассмотрим таблицу 3.2. Для определения среднего товарооборота найдем середины интервалов. Они будут следующими:
957 2671 4385 6099 7813 10381
Используя среднюю арифметическую взвешенную, определим средний розничный товарооборот для магазинов республики Калмыкия:
![]()
![]()
Рассмотрим таблицу 3.4. Для определения среднего грузооборота транспорта общего пользования найдем середины интервалов. Они будут следующими:
11,45 27,145 38,325 64,79 82,23 89,56 123,71
Используя среднюю арифметическую взвешенную, определим средний грузооборот транспорта общего пользования в республике Калмыкия:

Для таблицы 3.6 середины интервалов будут следующими:
2945 9945 18530
По средней арифметической определим среднюю месячную заработную плату населения республики Калмыкия:
![]() руб.
руб.
Средняя гармоническая (простая и взвешенная) применяется, когда расчет средней арифметической теряет смысл. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное от деления одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной:
 (5.2)
(5.2)
Средняя гармоническая простая применяется, когда веса всех вариантов равны:
 , (5.3)
, (5.3)
где ![]() - отдельные варианты;
- отдельные варианты;
![]() - число вариантов усредняемого признака.
- число вариантов усредняемого признака.
Средняя хронологическая применяется для моментного ряда с равными интервалами между датами (например, когда известны уровни на начало каждого месяца или квартала, года):
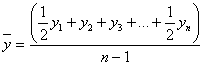 (5.4)
(5.4)
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отношение абсолютных показателей вариации к средней арифметической. Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.
Самым простым абсолютным показателем является размах вариации.
Размах показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признаками.
Его рассчитывают как разность между наибольшим и наименьшим значениями варьирующего признака (3.3).
Рассчитаем размах вариации для таблицы 3.2 по формуле (3.3):
![]() млн.руб
млн.руб
Рассчитаем размах вариации для таблицы 3.4 по формуле (3.3):
![]() млн.т.км
млн.т.км
Рассчитаем размах вариации для таблицы 3.6 по формуле (3.3):
![]() руб.
руб.
Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику. Для многих варьирующих признаков возможно допущение, что при прочих равных условиях все единицы совокупности в соответствии с основными законами своего развития имели бы одинаковую и притом вполне определенную величину признака в данных условиях места и времени. Вполне логично в качестве такой величины условно принять среднюю величину из всех значений признака, поскольку в ней более или менее погашаются случайные отклонения от закономерного хода развития явления, и средняя тем самым отражает типичный размер признака у данной однородной совокупности единиц. Но условия существования и развития отдельных единиц совокупности в определенной степени различны, что сказывается и на различии значений у них взятого нами признака. Средняя величина отражает эти средние условия.
Следовательно, средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. При обобщении этих колебаний необходимо вновь прибегнуть к методу средних величин – найти среднюю величину этих отклонений.
Такая средняя называется средним линейным отклонением. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант ![]() и
и ![]() (взвешенная или простая в зависимости от исходных условий) по следующим формулам:
(взвешенная или простая в зависимости от исходных условий) по следующим формулам:
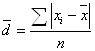 (простая), (5.5)
(простая), (5.5)
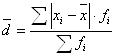 (взвешенная), (5.6)
(взвешенная), (5.6)
где ![]() - абсолютное значение отклонений.
- абсолютное значение отклонений.
Определим среднее линейное отклонение взвешенное для таблицы 3.2:
![]()
![]()
![]()
Таково в среднем отклонение вариантов признака от их средней величины. Это отклонение по сравнению со средней величиной признака очень большое. Оно отличается от средней на 419,95 млн.руб. Это свидетельствует о том, что данная совокупность в отношении нашего признака неоднородна, а средняя - -нетипична.
Определим среднее линейное отклонение взвешенное для таблицы 3.4:
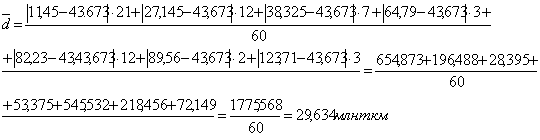
Определим среднее линейное отклонение взвешенное для таблицы 3.6:
![]()
![]()
![]()
![]()
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой (3.6) и взвешенной дисперсий (в зависимости от исходных данных):
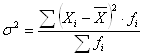 , (5.7)
, (5.7)
где ![]() - дисперсия;
- дисперсия;
![]() – среднее значение;
– среднее значение;
![]() – i-ый член совокупности;
– i-ый член совокупности;
![]() - частота.
- частота.
Существуют другие способы определения дисперсии. Вычисление дисперсии по средней арифметической:
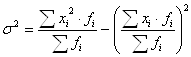 (5.8)
(5.8)
Дисперсия относительно условного нуля:
 , (5.9)
, (5.9)
где k – ширина этого интервала.
А – условный ноль, в качестве которого можно использовать середину интервала с наибольшей частотой.
Рассчитаем дисперсию по формулам (5.7), (5.8), (5.9) для таблица3:2

Рассчитаем дисперсию по формулам (5.7), (5.8), (5.9) для таблицы 3.4:



Рассчитаем дисперсию по формулам (5.7), (5.8), (5.9) для таблицы 3.6:

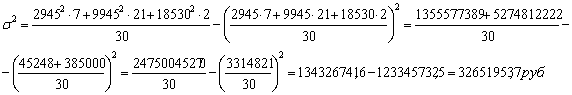

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
![]() (5.10)
(5.10)
Рассчитаем среднее квадратическое отклонение для таблицы 3.2:
![]()
![]()
Рассчитаем среднее квадратическое отклонение для таблицы 3.4:
![]()
Рассчитаем среднее квадратическое отклонение для таблицы 3.6:
![]()
В статистической практике часто возникает необходимость сравнения вариации различных признаков. При сравнении изменчивости различных признаков в совокупности для оценки интенсивности вариации, для сравнения ее в разных совокупностях и для разных признаков удобно применять относительные показатели вариации.
Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:
![]() , (5.11)
, (5.11)
где ![]() - коэффициент осцилляции;
- коэффициент осцилляции;
R – размах вариации.
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
 , (5.12)
, (5.12)
где ![]() - среднее линейное отклонение.
- среднее линейное отклонение.
Коэффициент вариации (3.4) – наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% для распределений, близких к нормальному. Коэффициент вариации применяется для сравнения колеблемости разнородных признаков.
Для таблицы 3.2 рассчитаем относительные показатели:
![]()
![]()
![]()
Коэффициент вариации превышает 33%, значит совокупность неоднородна.
Рассчитаем относительные показатели для таблицы 3.4:
![]()
![]()
![]()
Коэффициент вариации превышает 33%, значит совокупность неоднородна.
Рассчитаем относительные показатели для таблицы 3.6
![]()
![]()
![]()
Коэффициент вариации превышает 33%, значит совокупность неоднородна.
5. РАСЧЕТ И ПОСТРОЕНИЕ СТРУКТУРНЫХ ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯ 5.1 ОПРЕДЕЛЕНИЕ МОДЫ
Мода – значение признака, чаще всего встречающееся в совокупности. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой. В интервальном вариационном ряду с равными интервалами модальный интервал определяется по наибольшей частоте.
Мода определяется по следующей формуле:
![]() (6.1)
(6.1)
где Мо – мода;
![]() - нижняя граница модального интервала;
- нижняя граница модального интервала;
![]() - величина модального интервала;
- величина модального интервала;
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
![]() - частота интервала, последующего за модальным.
- частота интервала, последующего за модальным.
Для таблицы 3.2 рассчитаем моду. В данном распределении интервал 121-1814 будет модальным, так как он имеет наибольшую частоту. Определим моду:
![]()
Моду в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Абсцисса точки пересечения этих прямых и будет модой распределения. На рисунке 6.1 представлено графическое изображение моды для ряда распределения, представленного в таблице 3.2.
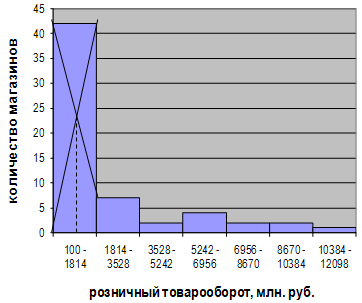
Рис. 6.1 Графическое определение моды по гистограмме
Для ряда распределения, представленного в таблице 3.4, определим моду. В данном распределении интервал 2,17-19,52 будет модальным, так как он имеет наибольшую частоту. Мода:
![]()
Графическое построение моды для данной совокупности представлено на рис. 6.2.
Для ряда распределения, представленного в таблице 3.6, определим моду. В данном распределении интервал15800-5460 будет модальным, так как он имеет наибольшую частоту. Мода:
![]()
Графическое построение моды для данной совокупности представлено на рис. 6.3.
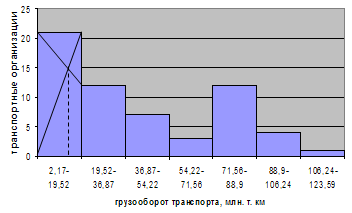
Рис. 6.2. Графическое определение моды по гистограмме
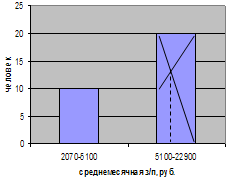
Рис. 6.3. Графическое определение моды по гистограмме
5.2 РАСЧЕТ МЕДИАНЫ
Медиана – значение изучаемого признака, приходящееся на середину ранжированной совокупности. При вычислении медианы интервального вариационного ряда сначала находят медианный интервал ![]() , где h – длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная частота, равная ½. Внутри найденного интервала расчет медианы производится по формуле:
, где h – длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная частота, равная ½. Внутри найденного интервала расчет медианы производится по формуле:
 , (6.2)
, (6.2)
где ![]() - медиана;
- медиана;
![]() - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
![]() - величина медианного интервала;
- величина медианного интервала;
![]() - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному;
![]() - частота медианного интервала;
- частота медианного интервала;
![]() - накопленная частота.
- накопленная частота.
Медиану в интервальном ряду можно определить графически. Медиана рассчитывается по кумуляте. Для ее определения из точки на шкале накопленных частот, соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.
Рассчитаем медиану для таблицы 3.2. Медианным будет интервал с границами (100 – 1814). Медиана:
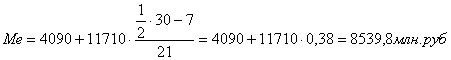
Рассчитаем медиану для таблицы 3.4. Медианным будет интервал с границами (2,17 – 19,52). Медиана:
Графическое построение моды для данного ряда представлено на рисунке 6.4.
Рассчитаем медиану для таблицы 3.6. Медианным будет интервал с границами (5100-22900). Медиана:
Графическое построение моды для данного ряда представлено на рисунке 6.5.
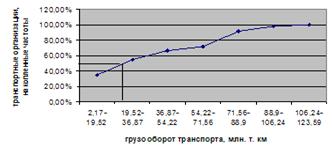
Рис. 6.4. Графическое определение медианы по кумуляте
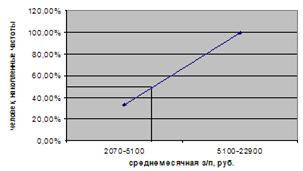
Рис. 6.5. Графическое определение медианы по кумуляте
5.3 РАСЧЕТ КВАРТИЛЕЙ
Квартили представляют собой значения признака, делящие ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний(Q3), отсекающий ¼ часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3 и остальные 25% превосходят Q3.
Для расчета квартилей по интервальному вариационному ряду используется формула:
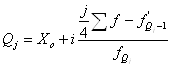 , (6.3)
, (6.3)
где ![]() - квартили;
- квартили;
![]() - нижняя граница интервала, содержащего квартиль;
- нижняя граница интервала, содержащего квартиль;
![]() - номер квартиля;
- номер квартиля;
![]() - частота интервала, содержащего квартиль;
- частота интервала, содержащего квартиль;
![]() -накопленная частота интервала, предшествующего интервалу, содержащему квартиль.
-накопленная частота интервала, предшествующего интервалу, содержащему квартиль.
Для таблицы 3.2 рассчитаем квартили. Первый квартиль находится в интервале 121 – 1814, накопленная частота которого равна 42 млн.руб. Второй квартиль также находится в интервале 121 – 1814. Третий квартиль лежит в интервале 1814 – 3528 с накопленной частотой 49 млн.руб. Четвертый квартиль находится в интервале 10384 – 12098 с накопленной частотой 60. с учетом этого получим:
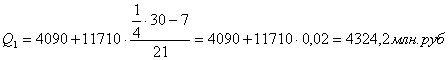
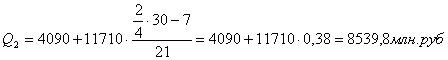
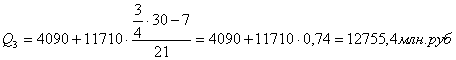
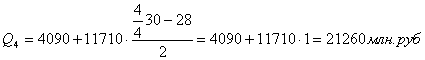
Для таблицы 3.4 рассчитаем квартили. Первый квартиль содержит 15 накопленных частот и входит в интервал (2,78-98,8).

Второй квартиль содержит 30 накопленных частот и входит в интервал (19,52 – 36,87).
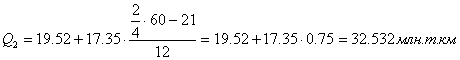
Третий квартиль содержит 45 накопленных частот и входит в интервал (71,56 – 88,9).
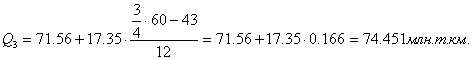
Четвертый квартиль входит в последний интервал (106,24 – 123,59).
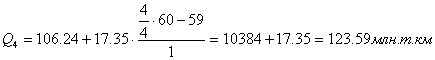
Для таблицы 3.6 рассчитаем квартили. Первый квартиль содержит 7,5 накопленных частот, поэтому входит в интервал (4090-15800).
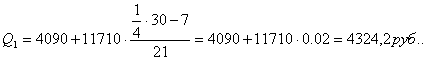
Второй квартиль содержит 15 накопленных частот, поэтому входит в интервал (4090-15800).
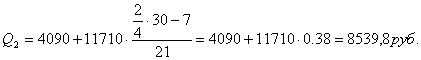
Третий квартиль содержит 22,5 накопленных частот, поэтому входит в интервал (4090-15800).
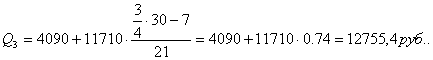
Четвертый квартиль входит в последний интервал (4090-11710).
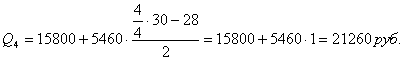
Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль делит совокупность в соотношении 1/10 к 9/10, второй дециль – в соотношении 2/10 к 8/10 и т.д.
Вычисляются децили по формуле:
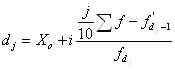 , (6.4)
, (6.4)
где ![]() - децили;
- децили;
![]() - номер децили;
- номер децили;
![]() - нижняя граница интервала, содержащего дециль;
- нижняя граница интервала, содержащего дециль;
![]() - частота интервала, содержащего дециль;
- частота интервала, содержащего дециль;
![]() -накопленная частота интервала, предшествующего интервалу, содержащему дециль.
-накопленная частота интервала, предшествующего интервалу, содержащему дециль.
Для таблицы 3.2 рассчитаем 1-й, 3-й, 6-й, 8-й, 9-й дециль. Первый, третий и шестой децили входят в интервал (121-1814), восьмой дециль входит в интервал 1814 – 3528, девятый дециль входит в интервал 5242 – 6956. С учетом этого получим:
![]()
![]()
![]()
![]()
![]()
Для таблицы 3.4 рассчитаем те же самые децили. Первый и третий децили содержат 6 и 18 накопленных частот соответственно и входят в интервал (2,78– 19,52).
![]()
![]()
Шестой дециль содержит 36 накопленных частот и входит в интервал (36,67– 54,22).
![]()
Восьмой и девятый перцентили содержат 48 и 54 накопленных частот соответственно и входят в интервал (71,56 – 88,9).
![]()
Для таблицы 3.6 также рассчитаем децили. Первый дециль содержит 3 накопленные частоты, поэтому входит в интервал (1800-4090).
![]()
Третий дециль содержит 9 накопленных частот, поэтому входит в интервал (2070-5010).
![]()
Шестой дециль содержит 18 накопленных частот, поэтому входит в интервал (4090-15800).
![]()
Восьмой дециль содержит 24 накопленных частот, поэтому входит в интервал (15800-21260).
![]()
Девятый дециль содержит 27 накопленных частот, поэтому входит в интервал (21260-22900).
![]()
Значения признака, делящие ряд на сто частей, называются перцентилями. Перцентили вычисляются по формуле:
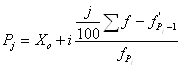 ,(6.5)
,(6.5)
где ![]() - перцентили;
- перцентили;
![]() - номер перцентиля.
- номер перцентиля.
Для таблицы 3.2 рассчитаем перцентили. 16-й, 23-й, 44-й перцентили входят в интервал (100-1814).
![]()
![]()
![]()
72-й, 77-й, 81-й перцентили входят в интервал (1814 – 35280).
![]()
![]()
![]()
83-й перцентиль содержит 83% накопленных частот и входит в интервал (3528 – 5242).
![]()
92-й, 95-й перцентили входят в интервал (6956 – 8670).
![]()
![]()
99-й перцентиль входит в интервал (10384 – 12098).
![]()
Для таблицы 3.4 рассчитаем 16, 23, 44, 72, 77, 81, 83, 92,95, 99 перцентиль по формуле (6.5):
16-й, 23-й перцентили входят в первый интервал 92,17 – 19,52.
![]()
![]()
44-й перцентиль содержит 26,4 накопленных частот и входит в интервал (19,52 – 36,87).
![]()
72-й, 77-й, 81-й, 83-й перцентили входят в интервал (71,56 – 88,9).
![]()
![]()
![]()
![]()
92-й, 95-й перцентили входят в интервал (88,9 – 106,24).
![]()
![]()
99-й перцентиль входит в интервал (106,24 – 123,59).
![]()
Для таблицы 3.6 рассчитаем 16, 23, 44, 72, 77, 81, 83, 92,95, 99 перцентиль по формуле (6.5). 16-й, 23-й перцентили входят в интервал (1800-4090).
![]()
![]()
44-й, 72-й, 77-й, 81-й, 83-й, 92-й, 95-й перцентили входят в интервал (4090-15800).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. ОБЩАЯ ХАРАКТЕРИСТИКА ИССЛЕДУЕМЫХ СТАТИСТИЧЕСКИХ СОВОКУПНОСТЕЙ 6.1 РАСЧЕТ ЦЕНТРАЛЬНЫХ МОМЕНТОВ
Центральным моментом порядка p распределения вариационного ряда называется среднее значение отклонений отдельных значений признака от его средней арифметической величины степени p.
Центральный момент первого порядка рассчитывается по формуле:
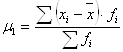 (7.1)
(7.1)
Центральный момент второго порядка рассчитывается по формуле:
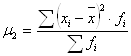 (7.2)
(7.2)
Центральный момент третьего порядка рассчитывается по формуле
 (7.3)
(7.3)
Центральный момент четвертого порядка рассчитывается по формуле:
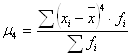 , (7.4)
, (7.4)
где ![]() - центральный момент четвертого порядка;
- центральный момент четвертого порядка;
![]() – среднее значение;
– среднее значение;
![]() – i-ый член совокупности;
– i-ый член совокупности;
![]() - частота.
- частота.
Для группировки, представленной в таблице 3.2, рассчитаем центральные моменты первого, второго, третьего, четвертого порядка по формулам (7.1), (7.2), (7.3), (7.4) соответственно:

![]()

![]()


Для группировки, представленной в таблице 3.4, также рассчитаем центральные моменты по формулам (7.1), (7.2), (7.3), (7.4):
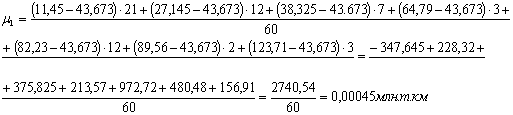



Для группировки, представленной в таблице 3.6, рассчитаем центральные моменты по формулам (7.1), (7.2), (7.3), (7.4):
![]()
![]()
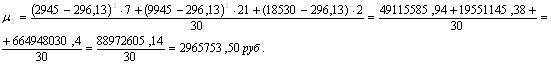


![]()
Для сравнительного изучения ассиметрии различных распределений вычисляется коэффициент ассиметрии:
![]() (7.5)
(7.5)
где As – ассиметрия;
![]() - среднее квадратическое отклонение в кубе.
- среднее квадратическое отклонение в кубе.
Для таблицы 3.2 рассчитаем среднее квадратическое отклонение в кубе:
![]()
Рассчитаем коэффициент ассиметрии по формуле (7.5):
![]()
Так как величина коэффициента ассиметрии положительная и больше 0,5, то ассиметрия данного распределения является правосторонней и значительной.
Для таблицы 3.4 рассчитаем среднее квадратическое отклонение в кубе:
![]()
Рассчитаем коэффициент ассиметрии по формуле (7.5):
![]()
вариационный медиана квартиль статистический
Величина коэффициента ассиметрии положительная и больше 0,5, значит ассиметрия данного распределения правосторонняя и значительная.
Для таблицы 3.6 рассчитаем среднее квадратическое отклонение в кубе:
![]()
Рассчитаем коэффициент ассиметрии по формуле (7.5):
![]()
Величина коэффициента ассиметрии отрицательная и больше 0,5, значит ассиметрия данного распределения левосторонняя и значительная.
6.3 РАСЧЕТ ЭКСЦЕССА РАСПРЕДЕЛЕНИЯ
Для симметричных и умеренно ассиметричных распределений рассчитывается показатель эксцесса распределения:
![]() , (7.6)
, (7.6)
где ![]() - среднее квадратическое отклонение в четвертой степени.
- среднее квадратическое отклонение в четвертой степени.
Для таблицы 3.2 рассчитаем эксцесс по формуле (7.6):
![]() млн.руб.
млн.руб.
Величина эксцесса положительная, значит данное распределение островершинное.
Для таблицы 3.4 рассчитаем эксцесс по формуле (7.6):
![]() млн.т.км
млн.т.км
Величина эксцесса отрицательная, следовательно, данное распределение плосковершинное.
Для таблицы 3.6 рассчитаем эксцесс по формуле (7.6):
![]() руб.
руб.
Величина эксцесса отрицательная, следовательно, данное распределение плосковершинное.
7. РАСПРЕДЕЛЕНИЕ ВЫБОРАЧНЫХ СРЕДНИХ
Похожие работы
... 3. география с/х 2. география промышленности 4. этнография 5. рекреационная география Вопрос: 40 Укажите, кто впервые употребил термин "экономическая география' Варианты ответов: 1. Аристотель 2. Ломоносов 3. Арсеньев 4. Самосский Размещение и развитие производительных сил общества Размещение производительных сил по территории страны предполагает научно-обоснованное размещение производства, ...
... экономической сферах, в обеспечении национальной безопасности и укреплении институтов государства. Именно «социальный заказ» общества и государства будет определять направления развития и изменения системы образования России в первом десятилетии 21 века»[7]. Конкретное же видение состояния и перспектив развития всей системы образования РФ и ее отдельных уровней отражено в документе «Федеральная ...
... ЦФО в национальной экономике страны характеризуется следующими данными (в % от общероссийских показателей): территория - 3,8, численность населения - 25,4, среднегодовая численность занятых в экономике - 27,2, валовой региональный продукт - 29,5, объем промышленной продукции - 19,9, сельского хозяйства - 23,4, растениеводства - 24,1, животноводства - 22,6, стоимость основных фондов в экономике - ...
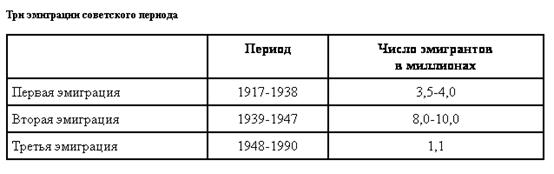
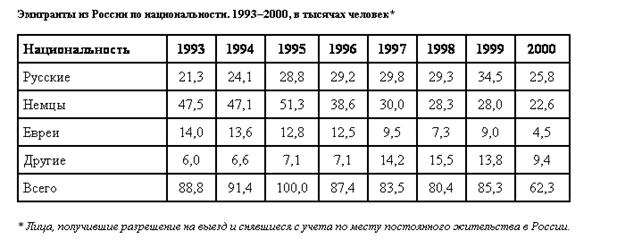
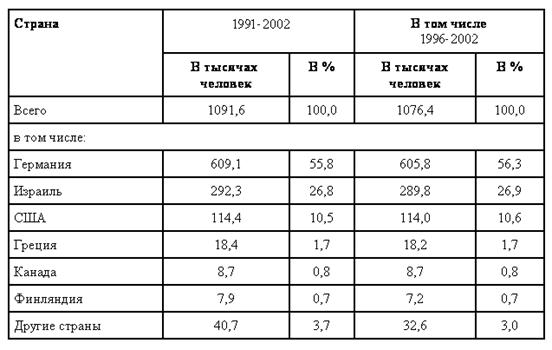
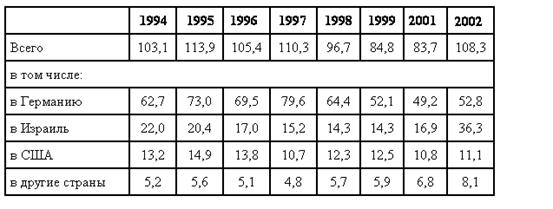
... Всего за 1989-2002 годы, по российским данным, из страны в дальнее зарубежье выехало на постоянное место жительства 1046 тысяч человек В "Демографическом ежегоднике России" и других официальных изданиях сведения о миграции между Российской Федерацией и странами вне СНГ и Балтии приводятся по данным МВД России. Число эмигрантов, или выбывших за пределы России, определяется как число лиц (включая ...

0 комментариев