ОПРЕДЕЛЕНИЕ ГРАНИЦ ГЕНЕРОЛЬНОЙ СОБСТВЕННО СЛУЧАЙНОЙ ВЫБОРКИ (ПОВТОРНЫЙ И БЕЗПОВТОРНЫЙ ОТБОР)

7.1 ОПРЕДЕЛЕНИЕ ГРАНИЦ ГЕНЕРОЛЬНОЙ СОБСТВЕННО СЛУЧАЙНОЙ ВЫБОРКИ (ПОВТОРНЫЙ И БЕЗПОВТОРНЫЙ ОТБОР)

Собственно-случайная выборка – отбор единиц из генеральной совокупности наугад или наудачу, без каких-либо элементов системности, прежде чем производить собственно-случайный отбор, необходимо убедится, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т. п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не выключение в нее отдельных единиц не вызывало сомнений.

Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.

Предельная ошибка выборки случайная величина.

 (8.1)

Средняя ошибка выборки.

 (8.2)

где -средняя ошибка выборки;

- генеральная дисперсия;

N – объем выборочной совокупности.

Предельная ошибка выборки в каких границах находится величина генеральной средней.

  (8.3)

Бесповторный отбор.

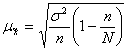 (8.4)

Средняя ошибка повторной собственно-случайной выборки определяется по формуле:

 (8.5)

Предположим, в результате выборочного обследования жилищных условий жителей Волгоградской области, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения.

Таблица.8.1

Группировка населения по жилой площади приходящегося на 1человека.

Общее число школ на 1 чел.	Число жителей
До 5	12	2,5	240	8294400
5-10	142,5	7,5	101531,25	2,09
10-15	1224	12,5	3121200	1,45
15-20	283,5	17,5	1339537,5	1,44
20-25	315	22,5	106312,5	1,12
25-30	195	27,5	103812,5	4,09
30-более	124,5	32,5	87668,75	10914759,38
Итого	2296.5		4860302.5	19209169.57

Первое действие определим среднюю выборочную.

Рассчитаем дисперсию.

Средне квадратическое.

 

Рассчитаем среднюю ошибку выборки.

Определим предельную ошибку выборки с вероятностью 0,954.

Установим границы генеральной средней.

Вывод: с вероятностью 0,954 можно заключить, что среднее число школ приходится, на одного человека лежит в пределах от 4858005.94 до 4858006,06

7.2 Определение границ генеральной средней типическим отбором

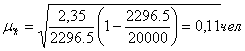
Типический отбор. Этот способ отбора используется в тех случаях. Когда все единицы генеральной совокупности можно разбить на несколько типических групп. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.

Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.

Отбор, пропорциональный дифференциации признака, дает лучшие результаты , однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.

Для бесповторного отбора.

  (8.5)

Пропорциональный бесповторный отбор.

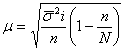 (8.6)

Таблица8.2

Результаты обследования рабочих предприятий.

п/п	Всего рабочих	Обследование	Число дней нетрудоспособных
			средняя	дисперсия
1	1000	100	18	49
2	1400	140	12	25
3	800	80	15	16
итого	3200	320	45	90

Рассчитать среднюю из внутригрупповую дисперсию.

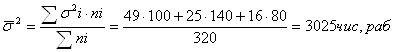
Определить среднюю и придельную ошибку выборки с вероятностью 0,954.

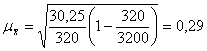
Рассчитать среднюю выборочную.

С вероятностью 0,954 можно сделать вывод о том, что среднее число дней временной нетрудоспособности одного рабочего в ценном по предприятиям. Находится в пределах.

Пропорциональна дифференсация вариационного признака.

Определяем не обходимый объем выборки по каждому предприятию.

 

По первому определению:

С учетом полученных значений рассчитаем среднюю ошибку выборки.

7.3 Определение границ генеральной с помощью серийной выборки

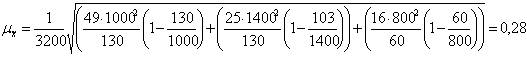
Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном либо механическом отборе серий, внутри которых производится сплошное обследование единиц.

Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

повторный отбор, (8.8)

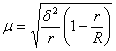бесповторный отбор, (8.9)

где  - число отобранных серий;

 - общее число серий.

Межгрупповую дисперсию вычисляют следующим образом:

 (8.10)

где  - средняя i-й серии;

 - общая средняя по всей выборочной совокупности.

Определим границы генеральной средней с помощью серийной выборки по данной нам задаче: В целях контроля качества комплектующих из партии изделий, упакованных в 55 ящиков, по 20 изделий в каждом. Была произведена серийная выборка (10%) по попавшим в выборку ящикам среднее отклонение параметров изделия от нормы соответственно составило (8, 11, 14, 10 и 13 мм) с предельной ошибкой выборки (1,6) определим среднее отклонение параметров во всей партии в целом.

Рассчитаем выборочную среднюю:

Определим величину межгрупповой дисперсии по формуле (8.10):

 

С учетом установленной вероятности предельная ошибка выборки составит:

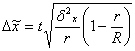 (8.11)

Подставим результаты в формулу (8.11):

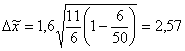
Произведенные расчеты позволяют сделать вывод, что среднее отклонение параметров всех изделий от нормы находятся в следующих границах 9,7512,65.

Для определения необходимого объема серийной выборки, при заданной предельной ошибки используются следующие формулы:

повторный отбор, (8.12)

бесповторный отбор, (8.13)

Подставим данные в формулы (8.12) и (8.13):

8. РАСЧЕТ ЭКОНОМИЧЕСКИХ ИНДЕКСОВ

 

В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве или сравнение фактических данных с любым эталоном (план, прогноз и т.д).

В международной практике индексы принято обозначать символами i и I (начальная буква латинского слова index). Буквой (i) обозначаются индивидуальные (частные) индексы, буквой (I) – общие индексы. Знак внизу справа означает период: 0 – базисный; 1 – отчетный. Помимо этого используются определенные символы для обозначения индексируемых показателей:

q – количество (объем) какого-либо товара в натуральном выражении;

p – цена единицы товара;

z – себестоимость единицы продукции;

t – затраты времени на производство единицы продукции;

w – выработка продукции в стоимостном выражении на одного рабочего или в единицу времени;

v – выработка продукции в натуральном выражении на одного рабочего или в единицу времени;

T – общии затраты времени (tq) или численность рабочих;

pq - стоимость продукции или товарооборота;

zq – издержки производства.

Все экономические индексы можно классифицировать по следующим признакам: степень охвата явления; база сравнения; вид весов (соизмерителя); форма построения; характер объекта исследования; объект исследования; состав явления; период исчисления.

По степени охвата явления индексы бывают индивидуальные и свободные. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. Их примером могут быть изменения объема производства отдельных видов продукции (телевизоров и т.д.), а также цен на акции какого-либо предприятия. Для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы (изменения физического объема продукции, включающей равноименные товары, индекса цен акций предприятий региона и т.п.), рассчитывают сводные, или общие, индексы. Если индексы охватывают не все элементы сложного явления, а только часть их, то такие индексы называются групповыми или субиндексами. По базе сравнения все индексы можно разделить на две группы: динамические и территориальные. При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий период, который называют базисным. Динамические индексы бывают базисные и цепные. Вторая группа индексов (территориальные) применяется для межрегиональных сравнений. Большое значение эти индексы имеют в международной статистике при сопоставлении показателей социально-экономического развития различных стран.

По виду весов индексы бывают с постоянными и переменными весами.

В зависимости от формы построения различаются индексы агрегатные и средние. Последние делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной формой экономических индексов. Средние индексы – производные, они получаются в результате преобразования агрегатных индексов.

По характеру объема исследования общие индексы подразделяются на индексы количественных (объемных) и качественных показателей. В основе такого деления индексов лежит вид индексируемой величины.

По объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т.д.

По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава. Деление индексов на эти две группы используется для анализа динамики средних показателей.

По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.

С помощью экономических индексов решаются следующие задачи: измерение динамики социально-экономического явления за два и более периодов времени; измерение динамики среднего экономического показателя; измерение соотношения показателей по разным регионам; определение степени влияния изменений значений одних показателей на динамику других; пересчет значения макроэкономических показателей из фактических цен в сопоставимые.

Каждая из этих задач решается с помощью различных индексов.

Рассмотрим таблицу (9.1) и определим цепные и базисные, индивидуальные индексы цен физического объема организации. Проверим взаимосвязь цепных и базисных индексов:

Таблица 9.1

Реализация по поставки угря в республику Калмыкия:

год	Цена за 1т, руб.	Произведено
2000	470	102,6
2001	550	108,5
2002	600	87,7
2003	750	109,9
2004	900	95,3
2005	1300	98,9
2006	1700	82,5

Индекс физического объема продукции рассчитывается по формуле:

 (9.1)

Подставим данные в формулу (9.1) и определим цепные индексы физического объема:

Подставим данные в формулу (9.1) и определим базисные индексы физического объема:

Индивидуальный индекс цен рассчитывается по формуле:

 (9.2)

Подставим данные в формулу (9.2) и определим цепные индексы цен:

Подставим данные в формулу (9.2) и определим базисные индексы цен:

Проверим базисные и цепные индексы.

Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные индексы. Например:

 (9.3)

Или

 (9.4)

Подставим данные в формулы (9.3) и (9.4):

1,04=1,04

Или

0,83=0,83

Зная последовательные значения базисных индексов, легко рассчитать на их основе цепные индексы:

 (9.5)

Или

 (9.6)

Подставим данные в формулы (9.5) и (9.6):

2,06=2,06

Или

2.02=2,02

Формирование системы индексов, например, цен или физического объема отличается от других систем индексов. Это связано с тем, что при построении систем этих индексов можно использовать постоянные и переменные веса.

Рассмотрим таблицу (9.2) и рассчитаем сводный индекс цен, товарооборота, физического объема реализации:

Таблица 9.2

Реализация продуктов в республики Калмыкия.

Продукт	2000 ()	2001 ()	2002 ()	2003 ()	2004 ()
Мясо	44	27	31	28	28
Сахар	24	24	24	26	31
Раст.масло	366	234	155	260	314
Хлеб	129	112	110	116	115
мука	10,5	16,7	15,3	18,4	1,9

продукт	2000		2001		2002		2003		2004
Мясо	2420	55	1998	74	2635	85	2744	98	3360	120
Сахар	312	13	432	18	552	23	676	26	961	31
Раст.масло	12444	34	9126	39	6510	42	14040	54	385	71
Хлеб	645	5	784	7	1100	10	1392	12	1610	14
мука	199,5	19	467,6	28	474,3	31	662,4	36	77,9	41

Индекс стоимости продукции или товарооборота представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде и определяется по формуле:

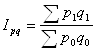 (9.7)

Подставим данные в формулу и получим:

Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции.

Индекс физического объема продукции – это индекс количественного показателя. В этом индексе индексируемой величиной будет количество продукции в натуральном выражении, а весом – цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема – индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид:

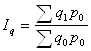 (9.8)

Подставим данные в формулу и получим:

Индекс физического объема продукции показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства.

Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, так как этот индекс характеризует изменение цен. Весом будет выступать количество произведенных товаров. Умножив цену товара на его количество, получаем величину, которую можно суммировать и которая представляет собой показатель, соизмеримый с другими подобными ему величинами. Индекс цен определяется по следующей формуле:

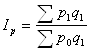 (9.9)

Подставим данные в формулу и получим:

Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен, или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен.

Рассмотрим таблицу (9.3) и рассчитаем индивидуальные и сводные индексы себестоимости, сводный индекс физического объема продукции и показать взаимосвязь сводных индексов:

Таблица 9.3

Реализация товаров в республики Калмыкия

Товар	2000 ()	2001 ()	2002 ()	2003 ()	2004 ()
Телевизор	4500	7600	9000	14000	18000
Холодильник	8500	9000	11000	15000	16000
Стир.машина	1500	6700	8000	9000	12000

Товар	2000		2001		2002		2003		2004
Телевиз.	3890	85	6400	94	7750	109	11400	156	13400	290
Холодил.	7640	100	8500	106	8200	208	9400	493	13900	540
Стир.маш.	950	84	5300	207	6200	237	7850	317	7290	406

Найдем индекс себестоимости:

 (9.10)

Подставим данные в формулу (9.10) и определим цепную и базисную себестоимость телевизора:

Цепная:

Базисная:

Подставим данные в формулу (9.10) и определим цепную и базисную себестоимость холодильника:

Цепная:

Базисная:

Подставим данные в формулу (9.10) и определим цепную и базисную себестоимость стиральной машины:

Цепная:

Базисная:

Определим себестоимость продукции по формуле:

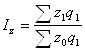 (9.11)

Подставим в формулу (9.11) и посчитаем:

Подставим данные в формулу (9.8) и получим:

9. КОРРЕЛЯЦИОННО – РЕГРЕССИОННЫЙ АНАЛИЗ

 

Корреляционно – регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ).

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции. Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определять «полезность» факторных признаков при построении уравнений множественной регрессии. Величина коэффициента корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям.

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значение. Регрессия может быть однофакторной (парной) и многофакторной (множественной).

Корреляционная зависимость является частным случаем стохастической зависимости, при которой изменение значений факторных признаков влечет за собой изменение среднего значения результативного признака. Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализов.

Основной предпосылкой применения корреляционного анализа является необходимостью подчинения совокупности значений всех факторных и результативного признаков к мерному нормальному закону распределения или близость к нему.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных. Основной предпосылкой регрессионного анализа является то, что только результативный признак подчиняется нормальному закону распределения, а факторные признаки могут иметь произвольный закон распределения.

По следующим данным о ВРП, численности активного населения и численности организаций необходимо определить зависимость между признаками:

Таблица 10.1

Расчетная таблица для определения уравнения регрессии

год	Числен.эк. акт.населения	Числен. Организаций	ВРП
2000 2000	1247	34529	41196,4	65352845,5	1563729	4529502374	74522736	3130178704	3567641711	116772,67
2001	1256	47203	65439,7	735294632,2	1578492	6875676648	75938464	3329751616	4784798369	113943,15
2002	1259	53717	151564,4	742298465,6	1598997	10887086017,44	81622899	3607323721	6266836813	170656,66
2003	1204	49563	426741.2	453712957,4	1375849	16543670332,84	79557451	3739444801	7865376152	123787,68
2004	1332	63702	163783,4	963465014,3	1783417	23820125641,29	84042210	3807507025	9523407779	184881,55
2005	1216	62147	193224,1	845392543,8	1246278	42371834673,64	83462363	4003978729	13025203443,4	155435,3
2006	1397	52784	234564,2	126543268,2	1838736	44502307362,49	65317164	2320252561	10161525113,3	85310,65
итого	11543	408015	85643,7	1347528794	12479103	164824246289.4	645387487	2547435267	64354789380,7	385787,66

Система нормальных уравнений имеет вид:

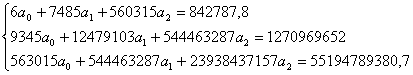
Таким образом:

С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле:

 (10.1)

Где - среднее значение соответствующего факторного признака;

- среднее значение результативного признака;

 - коэффициент регрессии при соответствующем факторном признаке.

Рассчитаем коэффициент эластичности:

Частный коэффициент детерминации:

 (10.2)

Где - парный коэффициент корреляции между результативным и i-м факторным признаками;

- соответствующий коэффициент уравнения множественной регрессии в стандартизированном масштабе.

Рассчитаем частный коэффициент детерминации:

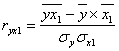
- частный коэффициент детерминации для фактора

Множественный коэффициент детерминации представляющий собой множественный коэффициент корреляции в квадрате, характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель. Для более точной оценки влияния каждого факторного признака на моделируемый используют  - коэффициент, определяемый по формуле:

 (10.3)

Где - коэффициент вариации соответствующего факторного признака.

ЗАКЛЮЧЕНИЕ

 

Анализ и обобщение статистических данных – заключительный этап статистического исследования, конечной целью которого является получение теоретических выводов и практических заключений о тенденциях и закономерностях изучаемых социально-экономических явлений и процессов.

Задачами статистического анализа являются: определение и оценка специфики и особенностей изучаемых явлений и процессов, изучение их структуры, взаимосвязей и закономерностей их развития.

В качестве этапов статистического анализа выделяются:

1) формулировка цели анализа;

2) критическая оценка данных;

3) сравнительная оценка и обеспечение сопоставимости данных;

4) формирование обобщающих показателей;

5) фиксация и обоснование существенных свойств, особенностей, сходств и различий, связей и закономерностей изучаемых явлений и процессов;

6) формулировка заключений, выводов и практических предложений о резервах и перспективах развития изучаемого явления.

Методы анализа должны меняться в зависимости от характера изучаемых процессов, их специфики, особенностей и форм проявления.

Статистический анализ данных проводится в неразрывной связи теоретического, качественного анализа сущности исследуемых явлений и соответствующего количественного инструментария изучения их структуры, связей и динамики.

Экономико-статистический анализ должен проводиться при строгом соблюдении следующих принципов, которые учитывают экономическую и статистическую их градацию.

Экономическими принципами являются: соответствие экономическим законам и положениям теории расширенного воспроизводства; адекватное отражение сущности экономической политики современного этапа общественно-экономического развития; ориентация на конечные экономические результаты; учет специфики изучаемого объекта, отрасли; согласование интересов субъектов различных иерархических уровней.

К статистическим принципам относятся: четко определенная цель экономико-статистического исследования; согласованность систем по горизонтали и вертикали; сопоставимость во времени и пространстве; логическая взаимосвязь между показателями, характеризующими объект или явление; комплексность и полнота отображения объекта исследования в статистических показателях; максимальная степень аналитичности.

Соблюдение данных принципов наряду с предпосылками применения методологии статистического анализа позволяет осуществить научно обоснованное экономико-статистическое исследование субъектов экономики в соответствии с принятой международной методологией.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.  Адамов В.Е. факторный индексный анализ (методология и проблемы). – М.: Статистика, 1997.

2.  Вайну Я.Я. Корреляция рядов динамики. – М.: Статистика, 1997.

3.  Джини К. Средние величины. – М.: Статистика, 1997.

4.  Ковалевский Г. В. Индексный метод в экономики. – М.: Финансы и статистика, 1989.

5.  Лившиц Ф.Д. Статистические таблицы. – М.: Госстатиздат, 1958.

6.  Миллс Ф Статистические методы. – М.: Госсстатиздат, 1958.

7.  Плошко В.Г., Елисеева И.И. История статистики. М.: Финансы и статистика, 1990.