Навигация
Інтегральні характеристики векторних полів
12525
знаков
0
таблиц
1
изображение
інтегральні характеристики векторних полів
1. Диференціальні операції другого порядку
Нехай в області 
задані скалярне поле 
і векторне поле 
, причому функції 
мають в області неперервні частинні похідні другого порядку. Тоді 
і 
є диференційовними векторними полями, а 
– диференційовним скалярним полем.
До векторних полів і можна застосувати операції обчислення дивергенції і ротора, а до скалярного поля 
– операцію обчислення градієнта. Таким чином, отримуємо повторні операції:
.
Операцію 
називають оператором Лапласа і позначають також символом 
:
.
З допомогою оператора Гамільтона оператор Лапласа записується у вигляді
.
Враховуючи, що
,
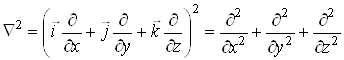дістаємо
.
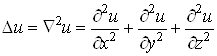Функція 
, яка задовольняє в деякій області рівняння Лапласа 
, називається гармонічною в цій області. Наприклад, лінійна функція 
є гармонічною в довільній області. Оператор Лапласа широко застосовується в рівняннях математичної фізики. Відзначимо, зокрема, що потенціал електричного поля точкового заряду або поля тяжіння точкової маси, який має вигляд 
, при 
задовольняє рівняння Лапласа:
(потенціальне векторне поле 
є безвихровим) і
(векторне поле 
є соленоїдальним).
1. Дві інші повторні операції 
і 
пов’язані співвідношенням
, (1)
де 
– вектор-функція, координатами якої є результати застосування оператора Лапласа до функцій 
.
2. Розкладання векторного поля на суму потенціального і соленоїдального полів
Довільне неперервно диференційовне векторне поле 
може бути зображено у вигляді
, (2)
де 
– потенціальне поле, 
– соленоїдальне поле.
Дійсно, за означенням потенціальне векторне поле є градієнтом деякого скалярного поля : 
. Тому для вектора із рівності (2) маємо
. (3)
Щоб векторне поле було соленоїдальним, воно має задовольняти умову 
, звідси, враховуючи рівність (3), знаходимо
.
Таким чином, для скалярного потенціала поля отримуємо рівняння
, (4)
де 
– відома функція даного поля .
Отже, якщо функція є розв’язком рівняння (4), то, поклавши , , отримаємо зображення поля у вигляді (2), де – потенціальне поле, – соленоїдальне поле.
Рівняння (2) – неоднорідне рівняння в частинних похідних другого порядку, яке називається рівнянням Пуассона:
.
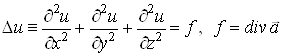Відзначимо, що це рівняння має (нескінченну) множину розв’язків, тому зображення поля у вигляді (2) не є єдиним.
Похожие работы
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
к джерела електричного поля представляють у виді еквівалентного електричного генератора. Під ним мається на увазі модельна фізична система, що повинна задовольняти двом вимогам: розрахункові потенціали електричного поля еквівалентного генератора в різних крапках організму повинні бути рівні реальним потенціалам; при варіюванні параметрів еквівалентного генератора повинні відбуватися такі ж зміни ...
... О. Костиков, В. Н. Голощапов, Г. К. Вороновский, А. Ю. Козлоков // Енергетика та електрифікація – 2007. – №9. – С. 17 – 21. АНОТАЦІЯ Альохіна С. В. Моделювання теплових процесів в елементах енергетичного обладнання ТЕС та АЄС шляхом розв’язання спряжених задач теплообміну. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.14.06 – технічна теплофі ...
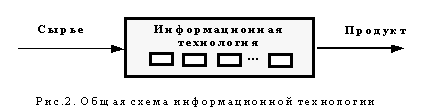
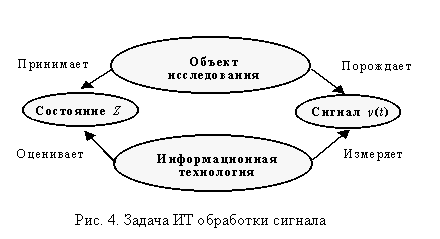
... сути, может приводить к необоснованному пессимизму в оценке практической ценности алгоритмов МГУА. Показано, что реалистичный подход к использованию алгоритмов самоорганизации в задаче синтеза ИТ обработки сигналов, основан на двухэтапном решении задачи. Первый этап предусматривает переход от исходного пространства наблюдений к обоснованному набору потенциально полезных признаков (потенциальных ...
0 комментариев