Навигация
Властивості потенціального поля
12525
знаков
0
таблиц
1
изображение
8. Властивості потенціального поля
Як відомо, векторне поле 
, яке задовольняє в області 
умову 
, називається потенціальним у цій області (
– скалярний потенціал поля ). Якщо поле 
потенціальне в області , то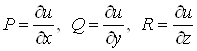 
і вираз 
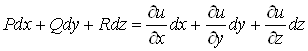є повним диференціалом функції в області . Це означає, що виконана умова незалежності криволінійного інтеграла від шляху інтегрування в просторі.
Таким чином, потенціальне в області поле має такі властивості.
1. Циркуляція потенціального поля вздовж довільного замкненого контуру 
дорівнює нулю:
.
2. Для довільних точок 
і 
області циркуляція потенціального поля 
вздовж кривої 
не залежить від вибору кривої 
і дорівнює різниці значень потенціала в точках і :
.
У випадку силового потенціального поля ця властивість означає, що робота такого поля вздовж кривої не залежить від вибору кривої, а залежить тільки від початкової і кінцевої точок і .
3. Потенціальне поле є безвихровим, тобто 
.
Нехай тепер дано векторне поле , яке задовольняє в області умову 
. Чи випливає звідси, що поле є потенціальним в області ? Відповідь на це запитання залежить від форми області . Якщо область є поверхнево однозв’язною, то із умови 
випливає, що існує функція 
така, що
.
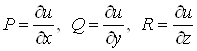Отже,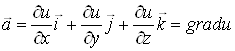 
, тобто поле 
є потенціальним в області .
Таким чином, умова є необхідною і достатньою умовою потенціальності поля у поверхнево однозв’язній області.
Потенціал потенціального поля у поверхнево однозв’язній області можна обчислити за формулою:
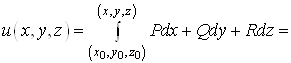
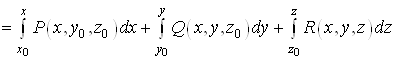. (14)
Якщо область не є поверхнево однозв’язною, то умова не є достатньою для потенціальності поля в області .
9. Інваріантне означення ротора
Нехай в області визначено векторне поле . Зафіксуємо точку 
і деяку площину, яка проходить через цю точку. Нехай 
– одиничний вектор нормалі до площини, 
– замкнений контур, який лежить в площині і обмежує область 
таку, що 
– внутрішня точка області . Запишемо формулу (12) для векторного поля в області . Застосовуючи до правої частини цієї формули теорему про середнє, отримуємо
,
диференціальне векторне поле формула соленоїдальне
звідки
,
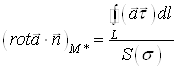де 
– площа області , 
– деяка точка області .
Стягуватимемо область до точки так, щоб залишалася внутрішньою точкою області . Тоді 
, а прямуватимемо до . Внаслідок неперервності 
значення 
прямуватимемо до 
. Таким чином, отримуємо
.
У праву частину формули входять величини, інваріантні відносно вибору системи координат (циркуляція векторного поля вздовж замкненого контура і площа плоскої області). Тому дана формула дає інваріантне означення проекції 
в точці на напрям, який виражається заданим вектором .
Отже, проекція ротора векторного поля на довільний напрям, а отже, і сам залежить тільки від векторного поля і не залежить від вибору системи координат.
Для означення вектора вищезазначеним способом достатньо розглянути в заданій точці проекції на три довільних некомпланарних напрями. Такими трьома проекціями визначається однозначно.
Размещено на http://www.
Похожие работы
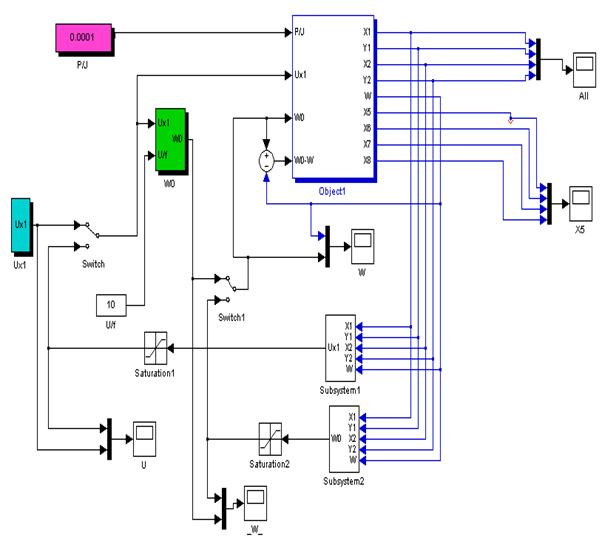
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
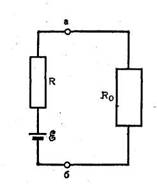
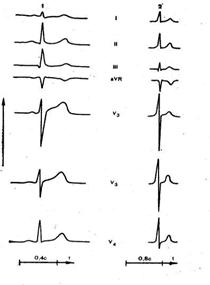
к джерела електричного поля представляють у виді еквівалентного електричного генератора. Під ним мається на увазі модельна фізична система, що повинна задовольняти двом вимогам: розрахункові потенціали електричного поля еквівалентного генератора в різних крапках організму повинні бути рівні реальним потенціалам; при варіюванні параметрів еквівалентного генератора повинні відбуватися такі ж зміни ...
... О. Костиков, В. Н. Голощапов, Г. К. Вороновский, А. Ю. Козлоков // Енергетика та електрифікація – 2007. – №9. – С. 17 – 21. АНОТАЦІЯ Альохіна С. В. Моделювання теплових процесів в елементах енергетичного обладнання ТЕС та АЄС шляхом розв’язання спряжених задач теплообміну. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.14.06 – технічна теплофі ...
... сути, может приводить к необоснованному пессимизму в оценке практической ценности алгоритмов МГУА. Показано, что реалистичный подход к использованию алгоритмов самоорганизации в задаче синтеза ИТ обработки сигналов, основан на двухэтапном решении задачи. Первый этап предусматривает переход от исходного пространства наблюдений к обоснованному набору потенциально полезных признаков (потенциальных ...
0 комментариев