Навигация
Белых 1) Событие А – появился
7 белых 1) Событие А – появился
3 черных белый шар. Р(А)=0,7
шаров Событие В – появился
черный шар. Р(В)=1/3
А и В – зависимые
Р(В) – условная вероятность
![]()
2)А-появился белый шар.Р(А)=0,7 (с возвратом)
В – появился черный шар. Р(В)=0,3
В данном случае ![]()
События А1, А2,…, Аn называются независимыми в совокупности, если каждое из них не зависит от произведения остальных событий и от каждого в отдельности.
Из попарной независимости не следует независимость в совокупности.
Если событие А1, А2,…, Аn – независимы, то ![]() 1,
1, ![]() 2,…,
2,…, ![]() n – независимы.
n – независимы.
Теорема
Вероятность совместного появления двух зависимых событий = произведению вероятности одного из них на условную вероятность другого.
![]()
В урне 7 белых, 3 черных шара. На удачу один за другим выбираем по одному шару без возврата. Найти вероятность того, что первый шар оказался белым, а второй черным.
![]()
Теорема
Вероятность совместного появления двух независимых событий = произведению вероятностей этих событий.
![]()
Вероятность появления только одного события
Пусть даны три независимых события А1, А2, А3; р1, р2, р3 – их вероятности. Найдем вероятность появления только одного из них.
B1=(только А1)=А1* ![]() 2*
2* ![]() 3
3
B2=(только А2)= ![]() 1* А2*
1* А2* ![]() 3
3
B3=(только А2)= ![]() 1*
1* ![]() 2* А3
2* А3
Т.к. В1, В2, В3 – несовместные, то
Р(только одного события)=Р(В1)+Р(В2)+Р(В3)
Т.к. А1, А2, А3 – независимые, то Ä1, Ä2, Ä3 тоже
независимые. Р(![]() 1)=q1; P(
1)=q1; P(![]() 2)=q2; P(
2)=q2; P(![]() 3)=q3
3)=q3
Р(только одного соб.)=p1*q2*q3+q1*p2*q3+q1*q2*p3
Вероятность попадания в цель при стрельбе из
трех орудий: Р1=0,7 Р2=0,8; Р3=0,9. Найти вероятность того, что только одно орудие поразило цель.Р1=0,8; Р2=0,7; Р3=0,9; q1=0,2; q2=0,3; q3= 0,1
Р(только одного события)= 0,7*0,2*0,1+0,3*0,8*0,1+0,3*0,2*0,9=0,092
Наивероятнейшее число появления события А в n независимых испытаниях
Пусть производится n независимых испытаний.
![]() ,
,
где р – вероятность появления события А при одном испытании, q – вероятность не появления события А при одном испытании.
Число k при котором данная вероятность окажется большей будет называться наивероятнейшим числом появления события А.
![]()
Если: 1) (n*p-q) – дробное число, существует одно наивероятнейшее число ![]() ; 2) (n*p-q) – целое число, то существуют два наивероятнейших числа
; 2) (n*p-q) – целое число, то существуют два наивероятнейших числа ![]() и
и ![]() ; 3) n*p – целое, то наивероятнейшее число
; 3) n*p – целое, то наивероятнейшее число ![]() .
.
Задача.
1) n=15; p=0,9; q=0,1
![]() 2) n=24; p=0,6; q=0,4
2) n=24; p=0,6; q=0,4
![]() 3) n=25; p=0,08; q=0,92
3) n=25; p=0,08; q=0,92
![]()
Вероятность суммы событий
Теорема. Вероятность появления одного из двух несовместных событий = сумме вероятностей этих событий.
![]()
Доказательство:
N – число всевозможных исходов испытания
М1 – число исходов, благоприятствующих событию А; М2 – число исходов, благоприятствующих событию В.
Т.к. события несовместные, то в них не будет общих благоприятствующих исходов.
![]() Мишень разделили на две области. Найти вероятность того, что стрелок попал в мишень.
Мишень разделили на две области. Найти вероятность того, что стрелок попал в мишень.
Соб. А – попадание в обл. А
А В Соб. В – попадание в обл. В
![]()
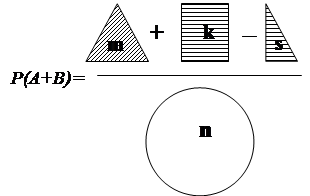
Теорема. Вероятность появления одного из двух совместных событий или обоих вместе = сумме вероятностей этих событий без вероятности их совместного появления.
![]()
Докажем с помощью диаграммы Венна.
Представим (А+В) и В через сумму двух несовместных событий. A+B=A+B* ![]()
B=A*B+B* ![]()
![]()
А А A+B=A+B-A*B
![]()
Аналогично с помощью диаграммы Венна можно доказать вероятность суммы трех совместных событий.
![]() Вероятность попадания в цель при стрельбе из
Вероятность попадания в цель при стрельбе из
трех орудий: Р1=0,8; Р2=0,7; Р3=0,9. Найти вероятность того, что цель будет поражена.
Событие А – цель поражена. Т.к. события совместные, то :
Р(А)=0,8+0,7+0,9-0,8*0,7-0,9*0,8-0,7*0,9+0,8*0,7*0,9=0,994
Формула полной вероятности
Событие А может произойти при условии появления одного из несовместных событий Н1, Н2,…, Нn, образующих полную группу событий. Их называют гипотезы.
Гипотезы исчерпывают все возможные предположения первого этапа опыта, а событие А это один из возможных исходов испытания второго этапа опыта.
Пусть известны вероятности гипотез: Р(Н1), Р(Н2), Р(Н3), …, Р(Нn) и условные вероятности события А:
![]()
Вероятность события А = сумме произведения вероятностей гипотез на соответствующие им условные вероятности.

Это Формула полной вероятности.
Задача. В двух ящиках содержится по 20 деталей, причем в первом 17 стандартных, а во втором 15 стандартных. Из второго ящика на удачу берется одна деталь и перекладывается в первый. Найти вероятность того, что извлеченная из первого ящика деталь окажется стандартной.
Гипотезы: Н1 – переложена стандартная деталь
Н2 – переложена нестандартная деталь
Р(Н1)=15/20
Р(Н2)=5/20
Событие А – из первого ящика извлекается стандартная деталь
![]()

Формулы Бейеса (вероятности гипотез)
Пусть событие А может произойти при условии появления одного из несовместных событий Н1, Н2, Н3,…,Нn, называемых гипотезами.
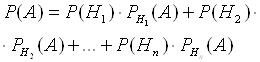
По этой формуле можно найти вероятность события А до проведении опыта.
Если событие А уже наступило (после проведения опыта) поставим задачу определить как при этом изменяются вероятности гипотез.
Найдем ![]() .
.

Аналогично можно получить формулы из остальных гипотез.
На 3-ех дочерей Алису, Бетти и Шарлоту в семье возложена обязанность мыть тарелки. Поскольку Алиса старшая ей приходится выполнять 40 % работы. Остальные 60 % делят между собой Бетти и Шарлота. Когда Алиса моет тарелку, вероятность для нее разбить тарелку 0,02, для Бетти 0,02, для Шарлоты 0,03. Родители не знают, кто вечером мыл посуду, но слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла а) Алиса, б) Бетти, в) Шарлота.
Событие А – тарелка разбита.
Гипотезы: Н1 – мыла Алиса; Н2 – мыла Бетти
Н3 – мыла Шарлота
Р(Н1)=0,4; Р(Н2)=0,3; Р(Н3)=0,3
![]() Т.к. событие А уже произошло, то необходимо применить вероятности гипотез.
Т.к. событие А уже произошло, то необходимо применить вероятности гипотез.

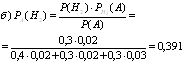
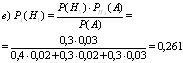
Вывод: формула Бейеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в результате которого появилось событие А. Отличие формулы полной вероятности от формулы Бейеса: формула полной вероятности применяется до опыта, а формула Бейеса после опыта.
Предельные теоремы в схеме Бернулли
![]()
Если n и k довольно большие
![]() , то в таких случаях для вычисления вероятностей применяют предельные теоремы.
, то в таких случаях для вычисления вероятностей применяют предельные теоремы.
Теорема Пуассона.
Если число испытаний n неограниченно увеличивается, т.е. ![]() и вероятность Р наступления события А в одном испытании уменьшается, т.е.
и вероятность Р наступления события А в одном испытании уменьшается, т.е. ![]() , но при этом число
, но при этом число ![]() , то вероятность того, что событие n наступит ровно k раз:
, то вероятность того, что событие n наступит ровно k раз:
![]() - асимптотическая формула Пуассона. Ее обычно используют, когда
- асимптотическая формула Пуассона. Ее обычно используют, когда ![]()
Некоторые электронные устройства выходят из строя, если откажет определенная микросхема. Вероятность ее отказа в течение одного часа работы устройства = 0,004. Какова вероятность того, что за 1000 часов работы придется 5 раз менять микросхему.
n=1000; p=0,004; ![]()
![]()
Если число n достаточно большое, а вероятность
Не стремится к 0, то для вычисления вероятность используются предельные формулы Муавра – Лапласа.
Интегральная теорема Муавра – Лапласа
Если вероятность Р наступления события А при независимых испытаниях постоянна и отлична от 0 и 1, то вероятность того, что при n независимых испытаниях событии А появится не менее k1 и не более k2 раз может быть найдена по приближенной формуле:
![]()
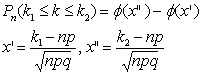
ф – функция Лапласа, значения в таблице
ф(-х)=-ф(х)
![]()
Задача.
Вероятность выпуска нестандартной лампы 0,1. Чему равна вероятность того, что в партии из 2000 ламп число стандартных не менее 1790?
p=0,9; n=2000; k1=1790; k2=2000
![]()

![]()
Среднее квадратическое отклонение дискретной случайной величины
Эта характеристика также как и дисперсия определяет рассеяние случайной величины Х вокруг ее математического ожидания. Дисперсия имеет размерность несовпадающую со значением случайной величины Х, а среднее квадратическое отклонение имеет размерность, совпадающую со значением случайной величины.
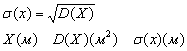
Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин = корню квадратному из суммы квадратов средних квадратических отклонений этих величин.
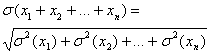
Доказательство:
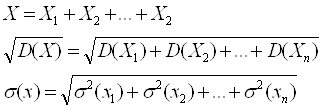
![]() Дифференциальная функция распределения случайной величины. Свойства
Дифференциальная функция распределения случайной величины. Свойства
![]() - плотность распределения вероятностей. Дифференциальная функция распределения существует только у непрерывной случайной величины.
- плотность распределения вероятностей. Дифференциальная функция распределения существует только у непрерывной случайной величины.
![]()
0 при ![]()
F(X) = k*X при ![]()
1 при ![]()
![]()
0 при ![]()
f(X) = k при ![]()
1 при ![]()
![]()
![]() F f(X)
F f(X)
Чтобы найти вероятность попадания случайной величины в интервал (a; b) с помощью дифференциальной функции используют функцию
![]()
Чтобы найти интегральную функцию распределения случайной величины используют:
![]()
Свойства.
1) ![]()
2) 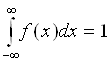
комбинаторика случайная величина вероятность математический
Математическое ожидание дискретной случайной величины. Свойства.
Математическое ожидание (среднее значение ДСВ) – постоянное число, равное сумме произведений значений случайных величин на их соответствующие вероятности.
![]()
Таблица
| Х | 2 | 3 | 5 |
| Р | 0,3 | 0,4 | 0,3 |
М(Х)=2*0,3+3*0,4+5*0,3=3,3
Свойства.
1) М(С)=С
2) М(СХ)=С*М(Х)
| Х | х1 | х2 | … | х3 |
| Р | Р1 | Р2 | … | Р3 |
![]()
| С*Х | С*х1 | С*х2 | … | С*х3 |
| Р | Р1 | Р2 | … | Р3 |
![]()
![]() 3) М(Х+У)=М(Х)+М(У) если Х и У -
3) М(Х+У)=М(Х)+М(У) если Х и У -
4) М(Х-У)=М(Х)-М(У) независимые
5) М(Х*У)=М(Х)*М(У) случ. Величины
Пример. Найти математическое ожидание М(Х+У) двумя способами.
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... оценками. Например, среднее арифметическое, медиана, мода могут показаться вполне приемлемыми для оценивания математического ожидания М (Х) совокупности. Чтобы решить, какая из статистик в данном множестве наилучшая, необходимо определить некоторые желаемые свойства таких оценок, т.е. указать условия, которым должны удовлетворять оценки. Такими условиями являются: несмещенность, эффективности ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...






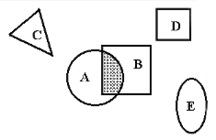


0 комментариев