Навигация
1. Х+У; М(Х+У)
2. М(Х)+М(У)
6) М(Х-М(Х))=0
(Х-М(Х)) – отклонение случайной величины от ее математического
Действия над дискретными случайными величинами
ДСВ можно 1) умножать на число,
2) возводить в степень.
1) умножение на число
2) возведение в степень
Две ДСВ называются независимыми, если событие Аi, состоящее в том, что случайная величина Х примет значения 
, 
и
событие
будут независимыми. В противном случае ДСВ называются зависимыми.
Несколько ДСВ называются взаимно независимыми, если закон распределения одной из них не зависит от того, какие ранее возможные значения приняли остальные величины.
Пример.
Если в верхней строке таблицы появляются одинаковые значения, то соответствующие столбцы объединяем и их вероятности складываем.
Действие вычитания и умножения выполняются аналогично.
Случайные величины
Дискретные случайные величины.
1) Случайной величиной называют величину, которая в результате испытания примет одно и только одно значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Случайные величины могут быть:
дискретные (прерывные), которые принимают лишь изолированные значения с определенными вероятностями. Их число может быть конечным и бесконечным (счетное). Пример: среди 100 новорож-денных число родившихся мальчиков от 1 до 10.
Непрерывные, которые могут принимать все значения из некоторого конечного промежутка. Пример: множество чисел принадлежащих промежутку
Дискретные случайные величины. Обозначаются заглавными буквами латинского алфавита X, Y,…, а их возможные значения х1, х2,…, хn.
Закон распределения ДСВ – Это соответствие между возможными значениями и их вероятностями. Его можно задать аналитически, таблично и графически, чаще всего задают таблицей:
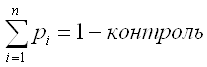
Задача. В денежно-вещевой лотерее выпущено 110 билетов. Разыгрывается приз 50000 рублей и 10 призов по 1000 рублей. Найти закон распределения случайной величины Х – стоимость выигрыша для владельца одного билета.
| Х | 500000 | 1000 | 0 |
| Р | 1/110 | 10/110 | 99/110 |
Дисперсия (рассеянное значение случайной величины вокруг математического ожидания этой величины)
Дисперсия – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
1) 
2) 
Пример.
| Х | 1 | 2 | 5 |
| Р | 0,3 | 0,5 | 0,2 |
М(Х)=1*0,3+2*0,5+5*0,2+5*0,2=2,3
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... оценками. Например, среднее арифметическое, медиана, мода могут показаться вполне приемлемыми для оценивания математического ожидания М (Х) совокупности. Чтобы решить, какая из статистик в данном множестве наилучшая, необходимо определить некоторые желаемые свойства таких оценок, т.е. указать условия, которым должны удовлетворять оценки. Такими условиями являются: несмещенность, эффективности ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
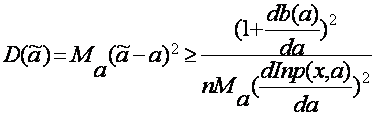
0 комментариев