Навигация
Приклади розв’язування задач
3. Приклади розв’язування задач
Задача 1. Обчислити визначник: 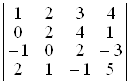 .
.
Розв’язання. I спосіб. Обчислимо визначник розкладанням за елементами (наприклад) третього рядка (властивість 10º):
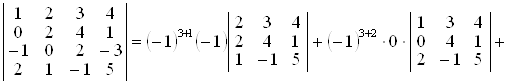
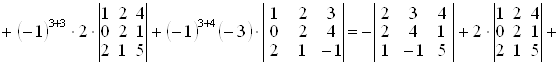
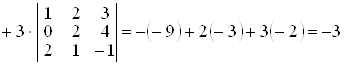 .
.
Визначники третього порядку, що входять до останнього виразу, обчислені за правилом трикутників.
II спосіб. Обчислимо визначник розкладанням за мінорами 2-го порядку (наприклад тими, що розташовані в 1-муі 2-мурядках вихідного визначника, властивість 12º). Усього таких мінорів буде шість (1-й, 2-й стовпці; 1-й, 3-й стовпці; 1-й, 4-й стовпці; 2-й, 3-й стовпці; 2-й, 4-й стовпці; 3-й, 4-й стовпці). Одержимо:
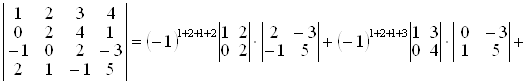
![]()
![]()
![]() .
.
III спосіб. Обчислимо визначник методом приведення визначника до трикутного вигляду. Для цього скористаємося властивістю 8°.
а) 1-й рядок додамо до 3-го рядка;
б) 1-й рядок, помножений на (–2), додамо до 4-горядка.
При цьому визначник не зміниться.
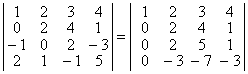
Далі: в) від 1-го рядка віднімемо 2-й рядок;
г) 2-й рядок, помножений на 3, додамо до 4-го рядка, помноженого на 2. При цьому визначник збільшиться вдвічі за рахунок множення 4-го рядка на 2.
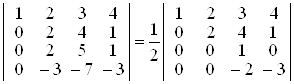 ;
;
д) в останньому визначнику 3-ій рядок помножимо на 2 і додамо до 4-го рядка. Визначник не зміниться. Одержимо:
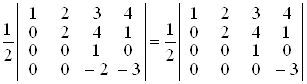 .
.
Визначник матриці трикутного вигляду обчислюється як добуток діагональних елементів. Доходимо висновку, що вихідний визначник дорівнює –3.
Задача 2. Обчислити визначник:  .
.
Рішення. Для обчислення визначника скористаємося методом виділення лінійних множників. Насамперед відзначимо, що вихідний визначник є багаточленом 4-го степеня відносно х. Крім того, при х = 2 перший і другий рядки співпадають, тобто визначник дорівнює нулеві. Отже, х = 2 є коренем багаточлена. Далі зауважуємо, що при х = 6, х = 12, х = 20 перший рядок співпадає з третім, четвертим і п’ятим рядком відповідно. Виходить, ми встановили всі чотири корені полінома, тобто
det А= C(x – 2)(x – 6)(x – 12)(x – 20).
Для знаходження C відзначимо, що у визначник множник х4 входить з коефіцієнтом, який дорівнює 1/24, а в багаточлен, що стоїть в правій частині, – з коефіцієнтом який дорівнює 1. Тоді C = 1/24. У такий спосіб:
det А = ![]() (x – 2)(x – 6)(x – 12)(x – 20).
(x – 2)(x – 6)(x – 12)(x – 20).
Задача 3. Обчислити визначник:  .
.
Рішення. Зрозуміло, що вихідний визначник можна одержати, якщо до всіх елементів визначника  додати х = 4. Тоді скористаємося методом зміни елементів визначника (властивість 13°). Одержуємо:
додати х = 4. Тоді скористаємося методом зміни елементів визначника (властивість 13°). Одержуємо:
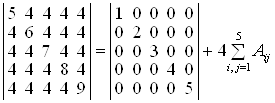 .
.
Визначник діагонального вигляду дорівнює добуткові діагональних елементів (5! = 120). Алгебраїчні доповнення дорівнюють: А11 = 5! = 120;
А22 = 3.4.5 = 60; А33 = 2.4.5 = 40; А44 = 2.3.5 = 30 і А55 = 2.3.4 = 24.
Решта Аij = 0. Одержуємо: det А = 120 + 4(120 + 60 + 40 + 30 + 24) = 120 + 4.274 = 1216.
Задача 4. Обчислити визначник n-го порядку  .
.
Рішення. Розкриємо визначник за елементами 1-го рядка:
 ,
,
а останній визначник розкриємо за елементами 1-го стовпця. Одержуємо:
Dn = 5Dn – 1 – 4Dn – 2. (*)
Записане співвідношення називається рекурентним співвідношенням і дозволяє виразити Dn через такі ж визначники більш низького порядку.
З (*) одержуємо:
1) Dn – Dn – 1 = 4(Dn – 1 – Dn – 2) = 42(Dn – 2 – Dn – 3) = … = 4n – 2 (D2 – D1) =
= 4n – 2 (21 – 5) = 4n .
2) Dn – 4Dn – 1 = Dn– 1 – 4Dn – 2 = Dn– 2 – 4Dn – 3 = … = D2 – 4D1 = 21 – 4.5 = 1.
3)
Маємо систему рівнянь: 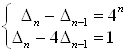 . Віднімаючи з 1-го рівняння 2-е, одержуємо: 3Dn – 1 = 4n – 1. У такий спосіб:
. Віднімаючи з 1-го рівняння 2-е, одержуємо: 3Dn – 1 = 4n – 1. У такий спосіб: 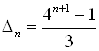 .
.
4. Задачі і вправи для самостійного розв’язування
1. Визначити число безладів у перестановках (за вихідне розташування завжди, якщо немає особливих вказівок, приймається розташування 1, 2, 3, ... у зростаючому порядку):
а) 2, 1, 5, 4, 3; б) 6, 3, 2, 5, 1, 4; в) 7, 5, 6, 4, 1, 3, 2;
г) 2, 1, 7, 9, 8, 6, 3, 5, 4; д) 9, 8, 7, 6, 5, 4, 3, 2, 1.
D а) 4; б) 10; в) 18; г) 18; д) 36. ▲
2. З'ясувати, які з наведених нижче добутків входять у визначники відповідних порядків і, якщо входять, то з яким знаком:
а) а43а21а35а12а54; б) а13а24а23а41а55;
в) а61а23а45а36а12а54; г) а32а43а14а51а66а25;
д) а27а36а51а74а25а43а62; е) а33а16а72а27а55а61а44;
ж) а12а23а34 …аn–1 n а25аkk (1 £ k £ n); з) а12а23а34 …аn-1nаn1n.
D а) –; б) не входить у визначник; в) +; г) +; д) не входить у визначник; е) +; ж) не входить у визначник; з) (–1)n. ▲
3. Вибрати значення i і k так, щоб наступні добутки входили у визначники відповідного порядку із зазначеним знаком:
а) а1iа32а4kа25а53 з « + »; б) а62аi5а33аk4а46а21 з « – »;
в) а47а63а1iа55а7kа24а31 з « + ».
D а) i = 1, k = 4; б) i = 5, k = 1; в) i = 6, k = 2. ▲
4. Користуючись тільки визначенням, знайти члени визначників, які мають у собі множники х4 і х3:
а) 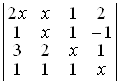 ; б)
; б) 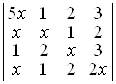 .
.
D а) 2х4, –х3; б) 10х4, –5х3. ▲
5. Знайти члени визначника 4-го порядку а) що містять елемент а32 і входять у визначник зі знаком « + »; б) що містять елемент а23 і входять у визначник зі знаком « – ».
D а) а11а24а32а43, а13а21а32а44, а14а23а32а41; б) а11а23а32а44, а12а23а34а41, а14а23а31а42. ▲
6. Виписати всі члени визначника 5-го порядку, що мають вигляд ![]() . Що вийде, якщо з їхньої суми винести а14а23 за дужки?
. Що вийде, якщо з їхньої суми винести а14а23 за дужки?
D 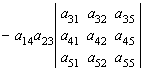 . ▲
. ▲
7. Як зміниться визначник n-гопорядку, якщо всі його стовпці записати в зворотному порядку? D Визначник помножиться на (–1)(n(n–1))/2. ▲
8. Не розкриваючи визначників, довести, що:
а) 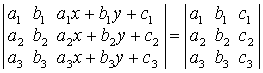 ;
;
б) 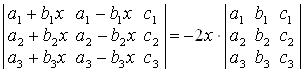 ;
;
в) 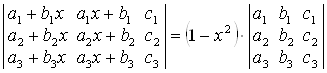 ;
;
г) 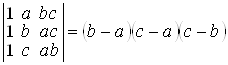 ; д)
; д) 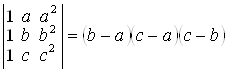 .
.
D а) властивості 7, 3; б) властивості 7, 3, 5; в) властивості 7, 3, 5; г) властивість 5;
д) властивість 5. ▲
9. Знайти мінори елементів а13, а24, а43 визначника 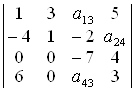 .
.
D М13 = 24; М24 = – 126; М43 = 52. ▲
10. Знайти алгебраїчне доповнення елементів а14, а23, а42 визначника
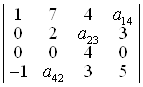 .
.
D А14 = 8; А23 = 0; А42 = – 12. ▲
11. Обчислити визначник, розкриваючи його по 3-му рядку 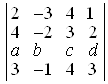 .
.
D 8a + 15b + 12c – 19d. ▲
12. Обчислити визначник, розкриваючи його по 2-му стовпцю: 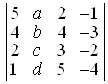 .
.
D 5a – 5b – 5c + 5d. ▲
13. Обчислити наступні визначники, знижуючи їхній порядок за допомогою розкладання за елементами деякого рядка або стовпця:
а) 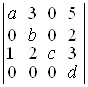 ; б)
; б) 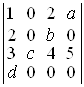 ; в)
; в)  .
.
D а) abcd; б) abcd; в) xyzuv. ▲
14. Обчислити наступні визначники 3-го порядку:
а) 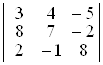 ; б)
; б) 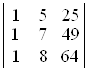 ; в)
; в) 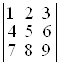 ;
;
г) 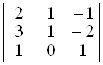 ; д)
; д) 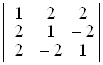 ; е)
; е) 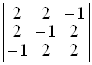 .
.
D а) 0; б) 6; в) 0; г) –2; д) –27; е) –27. ▲
15. Обчислити наступні визначники 3-го порядку:
а) 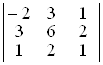 ; б)
; б) 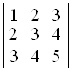 ; в)
; в) 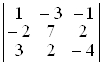 ;
;
г) 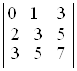 ; д)
; д) 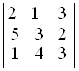 ; е)
; е) 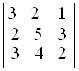 .
.
D а) –7; б) 0; в) –1; г) 4; д) 40; е) –3. ▲
16. Обчислити наступні визначники 3-го порядку:
а) 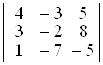 ; б)
; б) 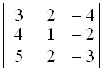 ; в)
; в) 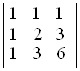 ;
;
г) 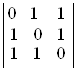 ; д)
; д) 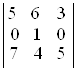 ; е)
; е) 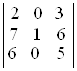 .
.
D а) 100; б) –5; в) 1; г) 2; д) 4; е) –8. ▲
17. Обчислити наступні визначники 3-го порядку:
а) 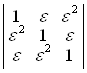 ; б)
; б) 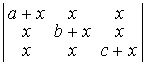 ; в)
; в) 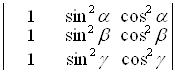 ;
;
г) 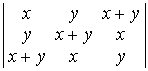 ; д)
; д)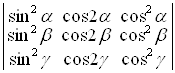 ;
;
е)  .
.
D а) (1 – e3)2; б) abc + x(ab + bc + ac); в) 0; г) –2(x3 + y3); д) 0; е) 0. ▲
18. Обчислити наступні визначники 4-го порядку:
а) 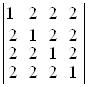 ; б)
; б) 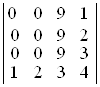 ; в)
; в)  ; г)
; г) 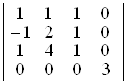 .
.
D а) –7; б) 0; в) –1; г) –18. ▲
19. Обчислити наступні визначники 4-го порядку:
а) 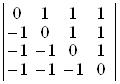 ; б)
; б) 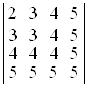 ; в)
; в) 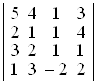 ; г)
; г) 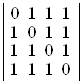 .
.
D а) 1; б) –5; в) 0; г) –3. ▲
20. Обчислити наступні визначники 4-го порядку:
а) 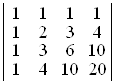 ; б)
; б) 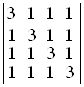 ;
;
в) 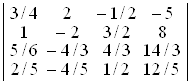 ; г)
; г)  .
.
D а) 1; б) 48; в) 1; г) 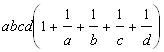 . ▲
. ▲
21. Обчислити визначники 4-го порядку:
а)  ; б)
; б) 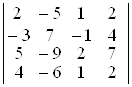 ; в)
; в) 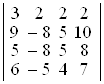 ; г)
; г) 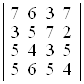 .
.
D а) –8; б) –9; в) –6; г) –10. ▲
22. Обчислити визначники 5-го порядку:
а) 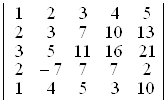 ; б)
; б) 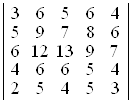 . D а) 52; б) 5. ▲
. D а) 52; б) 5. ▲
23. Зведенням до трикутного вигляду обчислити визначники:
а) 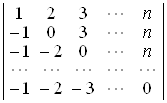 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
D а) n!; б) 2n + 1; в) хn(а0 + а1 + … + аn); г) ![]() . ▲
. ▲
24. Обчислити визначники методом виділення лінійних множників:
а)  ; б)
; б) 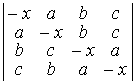 ;
;
в) 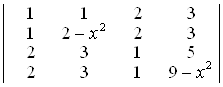 ; г)
; г)  .
.
D а) (х – 1)(х – 2)…(х – n +1); б) (x – a – b – c)(x – a + b + c)(x + a – b + c)(x + a + b – c);
в) (х2 – 1)(х2 – 4); г) x2z2, вказівка: визначник не зміниться, якщо 1-й стовпець поміняти місцями з 2-м стовпцем і одночасно 1-й рядок із 2-м рядком; при х = 0 визначник дорівнює 0, аналогічно по z. ▲
25. Розв’язати рівняння:
а)  ; б)
; б)  ;
;
в) ; г)
; г)  (х Î R).
(х Î R).
D а) хi = ai, i = 1, 2, … , n – 1; б) хi = ai, i = 1, 2, … , n; в) х = 0, 1, 2, … , n – 1; г) x = 1. ▲
26. Використовуючи метод рекурентних співвідношень, обчислити визначники: а)  ; б)
; б) 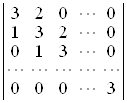 ; в)
; в)  .
.
D а) ![]() ; б) 2n + 1 – 1; в)
; б) 2n + 1 – 1; в) ![]() . ▲
. ▲
27. Обчислити визначники методом представлення їх у вигляді суми визначників:
а)  ; б)
; б)  .
.
∆ а) хn + (а1 + а2 + … + аn)хn – 1; б) вказівка: xi º (xi – ai + ai),
![]() . ▲
. ▲
28. Обчислити визначники методом зміни елементів визначника:
а)  ; б)
; б)  .
.
∆ а) ![]() ; б)
; б) ![]() . ▲
. ▲
29. Обчислити визначники n-го порядку:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
∆ а) 1; б) 3n; в) 1; г) хn; д) 1 – n; е) (–2)n –1(5n – 2). ▲
30. Обчислити визначники n-гопорядку:
а) 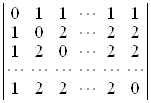 ; б)
; б) 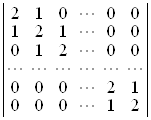 ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
∆ а) (–2)n –2(1 – n); б) n + 1; в) (–1)n –1(n – 1); г) 1; д) (1 – (–1)n)/2, вказівка:
Dn = 1– Dn –1; е) 0, якщо n = 2k +1; (–1)n/2, якщо n = 2k, kÎ Z; вказівка: Dn = – Dn – 2. ▲
31. Обчислити визначники n-го порядку:
а)  ; б)
; б) 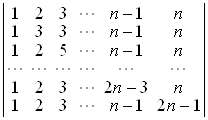 ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
∆ а) (b1 – а1)(b2 – а2) … (bn – аn); б) (n – 1)!; в) (–1)n – 1. n!; г) 0;
д) (–1)(n(n –1))/2nn–1(n + 1)/2; е) ![]() ▲
▲
Похожие работы
... часу електромашинного підсилювача Кп = 20 – коефіцієнт підсилення Отже передаточна функція ССП (без тахогенератора) буде мати такий вигляд: Kp(P) = Формалізована модель дослідження стійкості та якості перехідних процесів слідкувальної системи Формалізація приведення інформації зв’язаної з виділеними властивостями, до вибраної форми. внутрішні впливи; зовнішні впливи. ...
... лежащие на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит ...
... місцях по обсягам валюти балансу та обсягів балансового прибутку, за рівнем рентабельності активів та статутного капіталу ЗАТ КБ «Приватбанк» суттєво програє банкам, які спеціалізуються на роботі з юридичними особами. ВИСНОВКИ Досліджена в дипломному проекті фінансова діяльність комерційного банку – це діяльність, яка спричиняє зміни розміру та складу власного і залученого/запозиченого капіталу ...
... психічні процеси, формуються відповідні вміння і навички, – засобом формування загальнонавчальних умінь і навичок у нашому дослідженні вибрана дидактична гра. У процесі дослідження дидактичної гри як засобу формування загальнонавчальних умінь і навичок молодших школярів ми дійшли таких висновків: 1. У процесі аналізу психолого-педагогічної літератури встановлено, що уміння вчитися як володіння ...



0 комментариев