Навигация
Звено равномерно (ε=0) вращается вокруг оси, проходящей через центр тяжести (рис.4)
4. Звено равномерно (ε=0) вращается вокруг оси, проходящей через центр тяжести (рис.4).
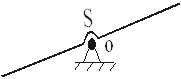
Рис.4
В этом случае сила инерции Fu=0, т.к. аS=0 и момент инерции µu=0 (т.к. ε=0).
Такое звено называется уравновешенным.
5. Звено неравномерно вращается вокруг оси, не проходящей через центр тяжести.
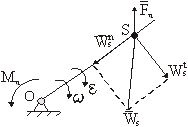
Рис.5
В этом случае возникает и сила инерции и момент сил инерции:
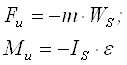
где: ![]() ; по величине
; по величине ![]()
Сила инерции приложена в центре тяжести и направлена противоположно ускорению центра тяжести WS. Момент пары сил инерции Mu направлен противоположно угловому ускорению.
Часто удобно силу инерции Fu и момент инерции Mu привести к одной равнодействующей силе Fu (рис.6). Для этого заменим момент Mu парой Fu и -Fu, момент которой равен: Fu·h=Mu.
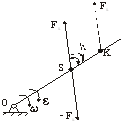
Рис. 6
Силу -Fu этой пары приложим в центре тяжести S. Тогда другая сила окажется приложенной в некоторой точке «К» звена. Силы Fu и -Fu, приложенные в центре тяжести взаимно уравновешиваются, и, таким образом, остается только одна сила, приложенная в точке «К» звена. Эта точка называется точкой качания.Положение точки качания определим из уравнения:

но: 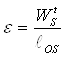
тогда: 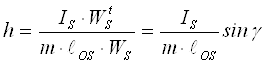 ;
;
Окончательно:  ;
;
Величина ℓSK для данного звена является величиной постоянной, не зависящей от его положения. Точка К всегда дальше от оси вращения, чем центр тяжести S.
6. Общий случай плоско-параллельного движения звена (рис.7).
Сила инерции: ![]() .
.
Сложное движение состоит из 2-х движений: из поступательного движения звена вместе с точкой А и вращательного движения звена относительно точки А. В соответствии с этим ускорение центра тяжести складывается из 2-х ускорений: ![]() .
.
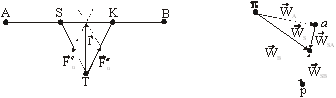
Рис.7
Тогда силы инерции звена в поступательном движении:
![]()
и силы инерции во вращательном движении:
![]()
Сила инерции в поступательном движении ![]() проходит через центр тяжести и направлена противоположно
проходит через центр тяжести и направлена противоположно ![]() .Сила инерции в относительном вращательном движении
.Сила инерции в относительном вращательном движении ![]() при учете момента сил инерции Мu проходит через точку качания «К» и направлена противоположно ускорению
при учете момента сил инерции Мu проходит через точку качания «К» и направлена противоположно ускорению ![]() . Следовательно сила
. Следовательно сила ![]() , являясь суммой сил
, являясь суммой сил ![]() и
и ![]() , проходит через точку пересечения Т линий действия этих сил и направлена противоположно ускорению центра тяжести WS.
, проходит через точку пересечения Т линий действия этих сил и направлена противоположно ускорению центра тяжести WS.
Для определения силы Fu и точки её приложения силы ![]() и
и ![]() находить не следует.
находить не следует.
Для определения точки Т следует из центра тяжести S провести прямую, параллельную ускорению ![]() , а через точку качания К - параллельную ускорению
, а через точку качания К - параллельную ускорению ![]() . Точка пересечения этих прямых и есть точка Т, через которую проходит сила инерции:
. Точка пересечения этих прямых и есть точка Т, через которую проходит сила инерции:![]() .
.
Положение точки К для всех положений звена одинаково.

4. Кинетостатический расчет механизмов
Силовой расчет механизмов ведем в предположении, что трение в кинематических парах отсутствует и все силы, действующие на звенья механизма, расположены в одной плоскости.
При отсутствии сил трения сила взаимодействия между 2-мя звеньями всегда направлена по нормали к поверхности их касания. В поступательной паре все элементарные силы взаимодействия и их равнодействующая будут расположены перпендикулярно направляющей поступательной пары.
Наиболее удобным методом силового расчета механизма является метод планов сил.
При силовом расчете механизм расчленяется на отдельные группы, при этом расчет начинается с группы, присоединенной последней в процессе образования механизма, а заканчивается расчетом ведущего звена начального механизма. Если плоский механизм имеет одну степень свободы, то начальный механизм состоит из 2-х звеньев: неподвижного (стойка) и начального звена. Эти звенья образуют либо вращательную кинематическую пару (кривошип-стойка), либо поступательную пару (ползун-направляющие). Звено, к которому приложена уравновешивающая сила Fу, будем считать при силовом расчете начальным звеном механизма. Реакция в начальном вращательном механизме зависит от способа передачи энергии начальному звену источником энергии. Если кривошипный вал приводится во вращение парой, например, непосредственно от электродвигателя, то в этом случае к валу приложен уравновешивающий момент.: Му=R3,2·h ![]() Нм
Нм![]() и реакция в опоре О вала (звено 1) будет равна действию звена 3 на звено 2 (кривошип) (рис.7).
и реакция в опоре О вала (звено 1) будет равна действию звена 3 на звено 2 (кривошип) (рис.7).
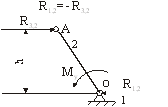
Рис.7
Рассмотрим на примере двухповодковой группы шатун АВ-ползун В кривошипно-ползунного механизма ДВС способ силового расчета, основанный на методе планов сил (рис.8).
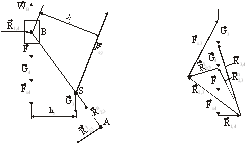
Рис.8
На звенья этой группы действуют силы:
F – давление газов на поршень;
G3, G4 – силы тяжести;
Fu3, Fu4 – результирующие силы инерции;
R1,4 – давление направляющих на ползун;
R2,3 – давление кривошипа на шатун.
Условие равновесия группы:
![]()
Раскладываем давление R2,3 на составляющие:
![]() , действующие:
, действующие:
![]() - вдоль оси звена 3 (шатун);
- вдоль оси звена 3 (шатун);
![]() - перпендикулярно к оси звена 3.
- перпендикулярно к оси звена 3.
Составляющую ![]() определим из уравнения моментов всех сил, действующих на шатун АВ, относительно точки В:
определим из уравнения моментов всех сил, действующих на шатун АВ, относительно точки В:
![]() или
или
![]()
откуда:
![]()
Строим план сил по уравнению равновесия группы.
Проводим вектор ![]() из начала вектора
из начала вектора ![]() . Через его начало проводим линию действия
. Через его начало проводим линию действия ![]() до пересечения с линией действия R1,4 ,
до пересечения с линией действия R1,4 ,
проведенной из конца вектора ![]()
![]() . R2,3 – давление в кинематической паре А.
. R2,3 – давление в кинематической паре А.
Планы сил строим в масштабе μр=500 Н/мм, 200 Н/мм, 100 Н/мм.
Давление R3,4 в паре шатун-ползун определяем из условия равновесия ползуна: ![]() .
.
Точкой приложения ![]() и
и ![]() будет точка В, т.к. силы F, Fu4 и G4, действующие на ползун, проходят через эту точку.
будет точка В, т.к. силы F, Fu4 и G4, действующие на ползун, проходят через эту точку.
Давление R1,2 в паре О-2 «Кривошип-стойка» и уравновешивающий момент Му определяем из условия равновесия кривошипа ОА (вес кривошипа и противовеса не учитываем, т.к. в большинстве положений он незначителен по сравнению с величиной R3,2).
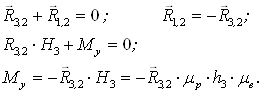
μр – масштаб плана сил;
h3 – плечо силы R3,2 относительно точки О на схеме механизма;
μе – масштаб длин кинематической схемы.
5. Теорема Н.Е. Жуковского
Если какой-либо механизм с одной степенью свободы под действием сил F1, F2, F3 …, приложенных в точках D, T, N…, находятся в равновесии, то в равновесии находится повернутый на 900 план скоростей, рассматриваемый как рычаг, вращающийся вокруг полюса Р и нагруженный теми же силами F1, F2, F3 …, приложенными в точках d, e, n….
Построение повернутого плана скоростей можно производить при помощи любого масштабного коэффициента μv, т.к. условие равновесия не зависит от величины плана.
Определим уравновешивающий момент Му для кривошипно-ползунного механизма (рис.9) и сравним его с величиной, полученной силовым расчетом механизма.
Для этого на план скоростей в изображающие точки переносим все заданные силы, включая силы инерции и уравновешивающую силу, повернутые на 900 в одном направлении.
Из условия равновесия плана скоростей как «жесткого рычага» определяем уравновешивающую силу Fу; её прикладываем в точке «а», считая её как бы приложенной в точке А кривошипа, и направляем её перпендикулярно линии кривошипа ОА.
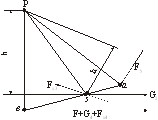
Рис.9
Следовательно,
![]() ;
;
Отсюда:
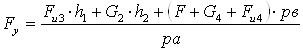 ;
;
Уравновешивающий момент:
![]()
![]() или
или ![]() ;
;
Величина расхождения:
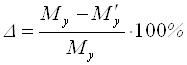
не должна превышать ± 5%.
механизм сопротивление инерция кинетостатический
Литература
1.Артоболевский И.И. Теория механизмов и машин М, 1975, с.268-271.
2.Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. Киев,1970, с.141-161.
Похожие работы
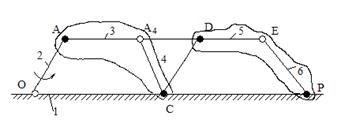
... для него план механизма. Построили диаграмму усилий, действующее на исполнительное звено, и если необходимо, построили 2 плана положений соответствующие началу и концу действия сил полезного сопротивления. Структурный анализ механизма 1. Выписываем кинематические пары определяя класс и вид 1–2 – вращ., 5 кл 2–3 – вращ., 5 кл 3–4 – поступ., 5 кл 4–1 – вращ., 5 кл 4–5 – вращ., 5 кл 5–6 – ...
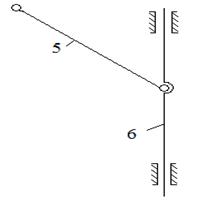
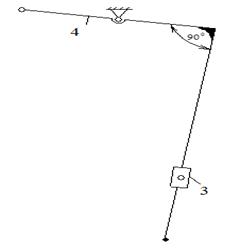
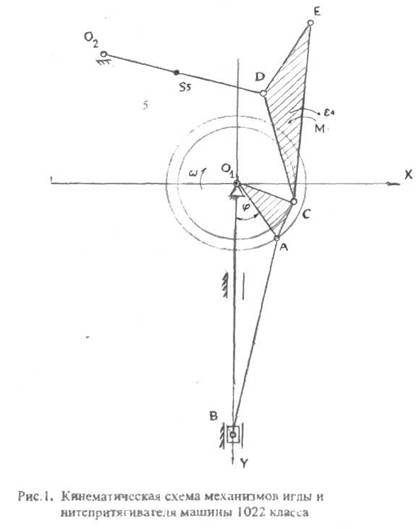
... исполнительных органов. Кинематическая схема может быть плоской или пространственной (в ортогональном или аксонометрическом изображении). На рис. I представлена плоская кинематическая схема механизмов иглы и нитепритягивателя универсальной швейной машины 1022 класса. На рис. 2 - пространственная конструктивно-кинематическая схема. Машина 1022 класса предназначена для стачивания деталей ...
... трением качения: а) платформа на катках (рис. 6.8) : f' = (k1 + k2 )/d ; (6.6) б) подшипник качения (рис. 6.9) : T = 0.5*Q*fs*d1; f' = beta*k* (1+ d1/d3) /d1 ; (6.7) для реальных конструкций подшипников beta = 1.4 - 1.6. 6.3. Коэффициенты полезного действия механизмов. 6.3.1. Коэффициент полезного действия - отношение полезной мощности на выходе Nn к мощности движущего усилия на ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
0 комментариев