Навигация
3.6 Описание алгоритмов
3.6.1 Программный модуль metod1.m
Исходный текст модуля metod1.m представлен в Приложении1.
Сначала производится инициализация переменных result (решение системы линейных алгебраических уравнений), temp (промежуточные значения решения системы линейных алгебраических уравнений на каждом шаге итерации), size_system (размерность системы), flag (флаг для остановки итерационного процесса), edop1 (абсолютное значение k-го и (k+1)-го решения), number_iter (количество итераций), time (время счета), number_oper (количество операций), a (матрица А системы Ax=b), b (столбец b системы Ax=b). После этого на дисплей выводится запрос допустимой погрешности. Когда погрешность введена, происходит очистка экрана, обнуление встроенного в MatLab счетчика операций с плавающей точкой, запоминание текущего момента времени.
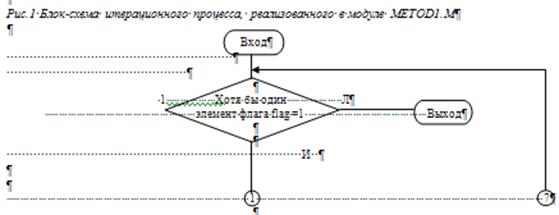
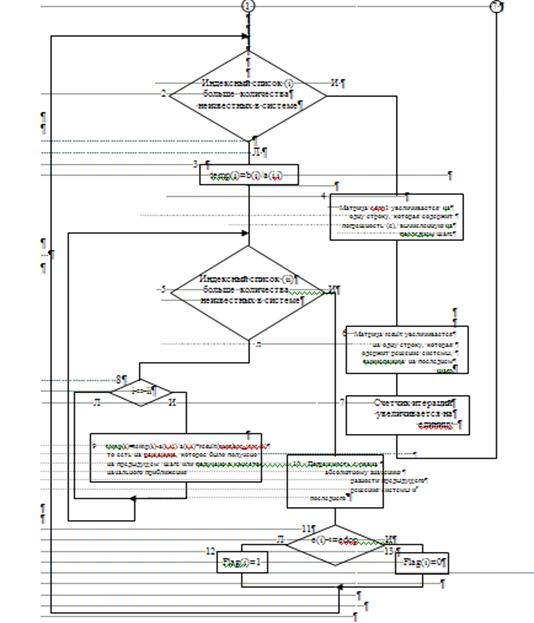
Далее после этих приготовлений запускается цикл перехода от системы вида F(x)=x к системе вида x=
(x) первым способом (см. п.2.2.) и решения системы линейных алгебраических уравнений методом простой итерации. Блок-схема цикла представлена на рис.1.
Как только заканчивается цикл итераций, происходит повторное запоминание текущего момента времени и количества операций с плавающей точкой. По окончании данных действий происходит подсчет времени счета, как разности ранее запомненных моментов времени. Далее происходит запись полученного решения в файл total.
Далее производится проверка, существует ли файл x_ok.m. Если таковой имеется, то высчитывается погрешность полученного решения и записывается в файл total.
После вышеописанных действий происходит последняя запись в файл total сведений о количестве шагов, необходимых для сходимости метода, времени счета, числе операций.
Затем происходит подготовка масштаба будущего графика итерационного процесса и непосредственно его построение, после которого выполнение программы прерывается до нажатия любой клавиши.
И наконец, когда какая-либо клавиша будет нажата, произойдет очистка экрана и построение графиков зависимости погрешности от шага итерации.
3.6.2 Программный модуль metod2.m
Исходный текст модуля metod2.m представлен в Приложении1.
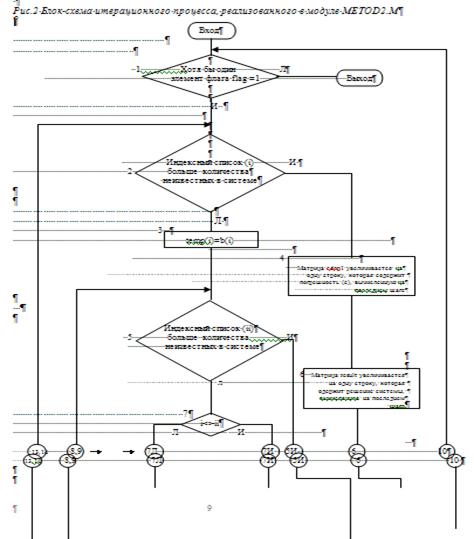
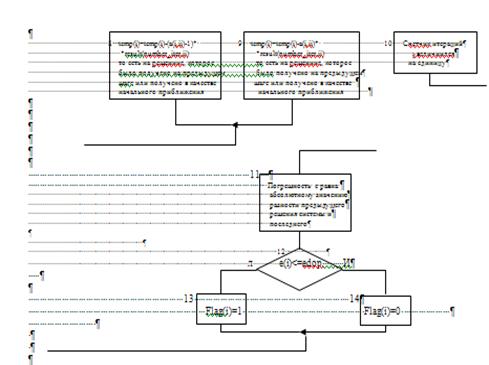
Алгоритм данного программного модуля аналогичен алгоритму модуля metod1.m. Единственное отличие - реализация цикла перехода от системы вида F(x)=x к системе вида x=(x) (см. п.2.2.) и решения системы линейных алгебраических уравнений методом простой итерации. Блок-схема цикла представлена на рис.2.
3.7 Используемые программные и технические средства
Все модули данного программного обеспечения написаны на языке MatLab в редакторе Norton Editor из комплекса утилит Norton Utilities 8.0.
Для правильной работы программ metod1 и metod2 необходима операционная система MS DOS (любой версии) или операционная система Windows95, программа MatLab 3.5f (или выше), а также персональный компьютер, совместимый с IBM PC 386SX (или выше).
4. Описание тестовых задач
В качестве тестовых задач рассмотрим две системы линейных алгебраических уравнений:
Cистема1
1,02x1 - 0,25x2 - 0,30 x3 =0,515
-0,41x1 + 1,13x2 - 0,15x3 =1,555 (4.1)
-0,25x1 - 0,14x2 + 1,21x3 =2,780
Точное решение: x1 =2,0 ; x2 =2,5 ; x3 =3,0 .
В качестве начального приближения x( 0 ) возьмем два вектора: x( 0)=(1000,1000,1000); x( 0 )=(1,1,1).
Система2
0,22x1 + 0,02x2 + 0,12x3 + 0,13x4 = -3
0,02x1 + 0,14x2 + 0,04x3 - 0,06x4 = 14
0,12x1 + 0,04x2 + 0,28x3 + 0,08x4 = 250 (4.2)
0,14x1 - 0,06x2 + 0,08x3 + 0,26x4 = -77
Точного решения нет.
В качестве начального приближения x( 0 ) возьмем два вектора: x( 0)=(0,10,20,30); x( 0 )=(-270,-503,1260,-653 ).
Все вычисления будем проводить при заданной точности 
=0.001 .
Похожие работы
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130. 4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...
... конкретной задаче (анализ) Составляя задачи на языке программирования Borland C++ Builder 6 для реализации точных методов решения СЛАУ я учитывал разное количество уравнений в системе (размерность матрицы задавал равным nxn). Но для проверки результатов использовал систему уравнений: Вообще говоря, процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, ...
0 комментариев