Навигация
Стренгл похож на Стрэддл, при разных ценах исполнения опционов. Более экономен, чем стрэддл
2. Стренгл похож на Стрэддл, при разных ценах исполнения опционов. Более экономен, чем стрэддл.
Покупка стрэнгла. Long Strangle. Данная стратегия заключается в покупке опционов колл и пут с одним сроком истечения контрактов, но разными ценами исполнения. Цена исполнения колла должна быть больше(В), чем пута(А). Используется, если ожидается, что цена базового актива изменится, волатильность повысится. (рис.6)
Продажа стрэнгла. Short Strangle. Данная стратегия заключается в продаже опционов колл и пут с одним сроком истечения контрактов, но разными ценами исполнения. Цена исполнения колла(В) должна быть больше, чем пута(А). Используется, если ожидается, что цена базового актива не изменится, волатильность понизится. (рис.7)
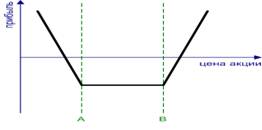
Рисунок 6 Покупка стрэнгла. Long Strangle
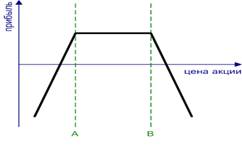
Рисунок 7 Продажа стрэнгла. Short Strangle
3. Стрэп - сочетание одного опциона пут и двух опционов колл с одинаковыми или с разными ценами исполнения – при предположении, что цена базисного актива пойдет вверх; (рис.8)
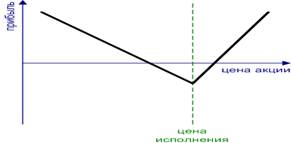
Рисунок 8 Стрэп. (Strap)
оценка опцион инвестиционный стоимость
4. Стрип комбинация из одного опциона колл и двух опционов пут с одинаковыми или с разными ценами исполнения, при вероятности снижения цены актива; Используется, если ожидается, что цена акции упадет с большой вероятностью, чем вырастет. (рис.9)
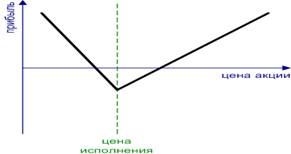
Рисунок 9 Стрип. Strip
5. Cинтетические фьючерсы – стратегия, при которой вместо базисного актива покупаются или продаются опционы (по характеру близка к стратегии покрытия опциона):
Синтетический короткий фьючерс. Synthetic Short Futures. – вместо продажи базового актива продается опцион колл и покупается опцион пут с одинаковыми ценами исполнения. При применении этой стратегии необходимо убедиться в тенденции рынка, так как и прибыль и убыток не ограничены. Расчет на снижение цены базисного актива. (рис.10)
Синтетический длинный фьючерс. Synthetic Long Futures. – покупка опциона колл и продажа опциона пут с одинаковыми ценами исполнения, при расчете на повышение цены базисного актива. прибыль и убыток не ограничены. (рис.11)
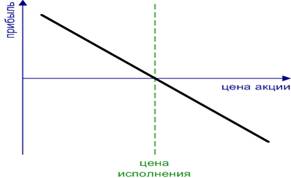
Рисунок 10 Синтетический короткий фьючерс
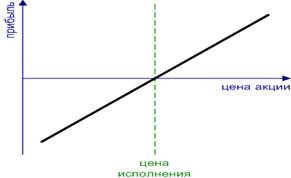
Рисунок 11 Синтетический длинный фьючерс
III. Спрэды (от англ spread- разница) – создаются из длинного и короткого опционов на один базовый актив, где оба опциона одинакового типа (либо Call, либо Put). Предназначены для ограничения риска, часто (но не всегда) ограничивают потенциал получения прибыли и убытков. Для данной опционной стратегии характерна заложенная инвестором разница в ценах или датах исполнения опционов.
1. вертикальный спрэд - комбинация, когда оба опциона имеют одинаковую дату истечения, но разную цену исполнения, за счет чего и формируется прибыль;
спрэд быка – сочетание покупки опциона колл с более низкой ценой исполнения с продажей опциона колл с более высокой ценой исполнения. Расчет на получение прибыли в ситуации падения цены базисного актива; (рис.12)
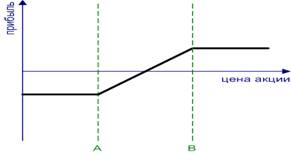
Рисунок 12 Бычий колл спрэд. Bull Call Spread
Покупка call опционов с ценой исполнения a и одновременная продажа другого колл опциона с большей ценой исполнения b. Разность премий даёт начальный убыток. Покупка put опциона с ценой исполнения a и одновременная продажа другого пут опциона с большей ценой исполнения b. Разность премий даёт начальную прибыль. Прибыль ограничена в обоих случаях: Call - разность между ценами исполнения минус начальный убыток; Put - начальная прибыль. Убыток ограничен в обоих случаях: Call -начальный убыток; put -разность между ценами исполнения минус начальная прибыль. Маржа может потребоваться. Фактор времени не особо важен, вследствие сбалансированной позиции.
спрэд медведя - одновременная покупка опциона колл и продажа такого же опциона колл, при цене исполнения меньшей, чем цена исполнения купленного опциона, в расчете на получение прибыли за счет роста цены базисного актива. Прибыльность сделки ограничена разницей в премиях двух опционов, риски колебания цены базисного актива снижаются.
Продажа колл опционов с меньшей ценой исполнения a и одновременная покупка другого колл опциона с большей ценой исполнения b. Разность премий даёт начальную прибыль:
Cash=M(Prsell-Prbuy),
Где M -размер опционного контракта; Pr — премия опциона. Продажа put опциона с меньшей ценой исполнения a и одновременная покупка другого пут опциона с большей ценой исполнения b.
Разность премий даёт начальный убыток:
Loss=M(Prsell-Prbuy),
Где M- размер опционного контракта; Pr- премия опциона. Прибыль: Ограничена в обоих случаях: Call - начальная прибыль; Put -разница между ценами исполнения минус начальный убыток. Убыток: Ограничен в обоих случаях: Call -разность между ценами исполнения минус начальная прибыль; Put- начальный убыток. Прибыли/убытки расcчитываются по формуле:
Prof=M(Prbuy-Prsell+(St-Ksell)+-(St-Kbuy)+),
Где M- размер опционного контракта; St - цена базового актива; K- цена исполнения; Pr - премия опциона. Маржа может потребоваться. Фактор времени не особо важен, вследствие сбалансированной позиции
Соответственно, put-спрэд «медведя» (рис.13) — сочетание покупки put опциона с высокой страйковой ценой и продажи пут-опциона с более низкой страйковой ценой и с единой датой истечения. Графики прибылей и убытков по put- и call-спрэдам выглядят аналогично.
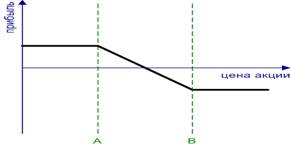
Рисунок 13 Медвежий пут спрэд. Bear Put Spread
обратный спрэд быка - одновременная продажа опциона пут и покупка опциона пут (с меньшей ценой исполнения, чем проданного опциона) на один базисный актив с одинаковым сроком исполнения, в расчете на рост базисного актива;
обратный спрэд медведя - покупка опциона пут и продажа опциона пут ( с более низкой ценой исполнения) на один базисный актив с одинаковым сроком исполнения. Расчет на снижение стоимости базисного актива;
Бэкспрэд - опционная стратегия, при которой продаются или покупаются длинные и короткие опционы, и количество длинных превышает количество коротких. Прибыль получают за счет существенного снижения либо повышения цены базисного актива;
Рейтио спрэд противоположен предыдущей опционной стратегии, количество коротких опционов превышает количество длинных, в расчете на небольшое изменение цены базисного актива;
Спрэд бабочка (сэндвич) – комбинация опционов с тремя различными ценами исполнения – для получения небольшой прибыли при незначительных изменениях цены базисного актива и страхования рисков значительного колебания цены;
Спрэд кондор заключается в приобретении опциона колл с более низкой ценой исполнения, и одновременно продаже двух опционов колл с более высокими, но отличными друг от друга ценами исполнения и в приобретении опциона колл с самой высокой ценой исполнения – всего 4 опциона.
2. Временной (календарный) спрэд состоит из двух опционов с одинаковой ценой, но разными датами исполнения. Тоже может быть бычьим и медвежьим, длинным и коротким;
3. Диагональный спрэд - это смесь спрэдов, состоит из опционов с разными сроками истечения и разными ценами исполнения;
4. Пропорциональный спрэд - стратегия, при которой количество покупаемых опционов отличается от количества продаваемых.
В общем виде использование опционов имеет такие плюсы, как ограничение риска покупателя опциона при теоретически неограниченной прибыли, высокая доходность сделок, возможность оперировать относительно небольшими денежными средствами. Имеющиеся же недостатки вполне возможно снизить при помощи формирования подходящей конкретному инвестору опционных стратегий, которые можно применять как для хеджирования, так и для спекуляций.
Глава 2. Модели оценки стоимости опционов
2.1 Методики расчета стоимости опционаСуществует несколько методик, которые позволяют провести расчет стоимости опциона.
Стоимость выбора можно определить с помощью теории оценки опционов и связанного с ней ситуационного подхода (contingent claims analysis). Однако часто такая процедура оценки становится чрезвычайно сложной, и возникает необходимость заменить ее качественными суждениями.
Применение теории оценки опционов для принятия решений — серьезный шаг вперед в развитии теории капитального бюджета, и менеджеры, занимающиеся составлением капитального бюджета на фирмах, должны понимать, когда и как можно с пользой для дела применить эти концепции.
Следует различать два типа ситуаций:
В ситуациях первого типа имеется достаточно большое количество ценных бумаг или активов, так что доходы от конкретного оцениваемого опциона можно в точности воспроизвести, купив портфель, состоящий из одной или нескольких ценных бумаг или активов. Эту ситуацию рассмотрим в первую очередь.
В ситуациях второго типа оцениваемые варианты нельзя в точности воспроизвести с помощью воображаемого портфеля ценных бумаг или других активов. Но и в исследование подобных ситуаций теория опционов также внесла значительный вклад, поскольку привлекает внимание к их существованию и к необходимости оценить выбор в этих ситуациях.
Теоретическая стоимость опциона — это тот выигрыш, который можно было бы получить, если исполнить опцион сразу. Если рыночная стоимость обыкновенной акции больше, чем цена исполнения опциона, выигрыш — это разница между ценой акции и ценой исполнения (расходами на сделку пренебрегаем). Если рыночная стоимость акции ниже цены исполнения, то теоретическая стоимость равна нулю (исполнять опцион попросту неразумно).
Пусть
Cmin - минимальная (теоретическая) стоимость опциона;
S — рыночная стоимость обыкновенной акции;
К — цена исполнения.
Тогда теоретическая стоимость опциона будет равна S - К, если S >К и 0, если S £ К.
Теоретическая стоимость ни в коем случае не является теоретически верной ценой опциона, но она устанавливает нижнюю границу стоимости опциона, если исполнить его сразу и немедленно обратить полученный выигрыш в деньги. Рыночная стоимость опциона будет либо равна теоретической, либо больше ее.
В настоящее время теория опционов развивается в направлении реальных активов.
Термин «реальный опцион» (real option) введен Стюартом Майерсом в 1977 году [Myers, 1977] по аналогии с обычным (финансовым) опционом в контексте анализа финансовой политики фирмы, а потому изначально был заключен в кавычки. Основанием для аналогии послужила общая для всех опционов (финансовых и реальных) черта – право без обязанности или (как вариант) возможность без необходимости. Другие черты финансовых опционов, а именно: фиксированный срок истечения, предмет совершаемой сделки (купля или продажа финансового актива) и заранее оговоренная цена исполнения – не обязательны. В реальном опционе они могут быть представлены в стертом или измененном виде или вообще отсутствовать. Метод реальных опционов рассматривает методологию хеджирования портфелей, включающих не только ценные бумаги, но и инвестиционные проекты, предполагающие имущественные вложения в различные активы.
Модель реальных опционов предоставляет менеджерам возможность планирования и управления стратегическими инвестициями и представляет синтез оценки рыночной стоимости и принятия инвестиционных решений в условиях неопределенности. Так, модель реальных опционов объединяет методику проектного анализа и формирования корпоративной стратегии.
Для оценки как реальных, так и обычных опционов применяются в основном две модели:
· Биноминальная модель;
· Модель Блека-Шоулза.
Эти модели играют большую роль в инвестиционном анализе. Рассмотрим и дадим оценку каждой из них.
2.2 Биноминальная модель оценки опционаДля оценки стоимости опциона «колл» или «пут» можно использовать биноминальную модель оценки стоимости опциона (ВОРМ). Лучше всего представить ее на примере европейского опциона (European option), т.е. опциона, который может быть исполнен только в день его истечения. В этом случае мы предполагаем, что по базисной акции не выплачиваются дивиденды в течение срока действия опциона. Модель также можно модифицировать для оценки стоимости американского опциона (American option), т.е. опциона, который можно исполнить в любое время в течение срока действия опциона. Модель также можно использовать для оценки стоимости опционов на акции, по которым выплачиваются дивиденды в течение срока опционного контракта.
Биномиальный метод, называемый также по имени его авторов методом Кокса-Росса-Рубинштейна (Cox-Ross-Rubinstein), был предложен в 1979 году и является более поздним по отношению к методу Блэка- Шоулса (1973). Однако начинать знакомство с подходами к оценке опционов лучше именно с более простого биномиального метода. В определенном смысле он аналогичен численным методам решения дифференциальных уравнений. Первоначально данный подход применялся для расчета стоимостей американских опционов, для которых отсутствует точное аналитическое решение, а впоследствии был распространен на многие более сложные производные инструменты. В настоящее время численные методы наряду с методами статистических испытаний (Монте-Карло) чаще всего используются в моделях обсчета производных инструментов, так как позволяют максимально учесть реальные условия операций с ними.
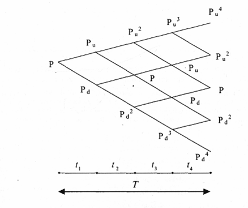
В биноминальной модели весь период действия опционного контракта разбивается на ряд интервалов времени; в рассматриваемом ниже случае – на два периода. Предполагается, что стоимость опциона и стоимость базового актива (в данном случае акции) изменяется согласно разветвленной системе на рис.14. Учитывая данные о стандартном отклонении курса базисного актива, получают значения его цены для каждого интервала времени (строят дерево распределения цены). Так же определяют вероятность повышения и понижения курсовой стоимости актива на каждом отрезке временного интервала. Имея значения цен актива к моменту истечения срока действия опциона, определяют его возможные цены в данное время. После этого последовательным дисконтированием цен опциона (с учетом вероятности повышения и понижения стоимости актива на каждом интервале времени) получают значение его цены в момент заключения контракта.
![]()
![]()
uS0 Сu1
![]() S0 С0
S0 С0
![]()
dS0 Сd1
Рисунок 14 Биноминальная модель ценообразования опционов
Техника построения биномиальной модели является более громоздкой, чем метод Блэка—Шоулза, но позволяет получить более точные результаты, когда существует несколько источников неопределенности или большое количество дат принятия решения.
В основе модели лежат два допущения:
·в одном интервале времени могут быть только два варианта развития событий (худший и лучший);
·инвесторы нейтрально относятся к риску.
Простейший пример использования биномиальной модели для расчета стоимости инвестиционного проекта уже был использован выше. Напомним, что мы рассматривали проект с одним интервалом времени и двумя вариантами реализации решений. Для каждого варианта была оценена вероятность наступления и рассчитана стоимость реального опциона. Вычисление стоимости опциона данным методом, по сути, представляет собой движение по «дереву решений», где в каждой точке менеджеры стараются принять наилучшие решения. В итоге денежные потоки, возникающие как следствие будущих решений, сводятся к приведенной стоимости. Однако в реальной жизни «дерево решений», как правило, имеет гораздо больше узлов принятия решений (рис.15)
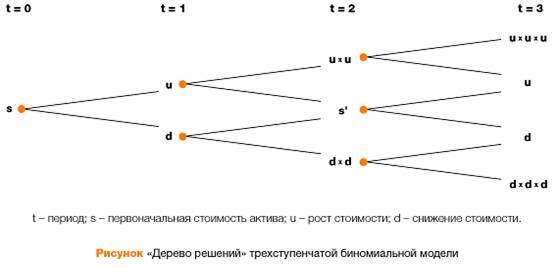
При построении «дерева решений» с большим количеством дат принятия решений применяются те же принципы расчета стоимости реального опциона, что и для рассмотренной выше одноступенчатой модели. Однако чем больше узлов принятия решений, тем сложнее сделать оценку.
На практике основные трудности использования биномиальной модели связаны с определением значений относительного роста и снижения стоимости бизнеса в каждом периоде, а также вероятностей положительного и негативного варианта развития событий. Для расчета этих параметров разработаны соответствующие формулы. Возможный рост стоимости бизнеса рассчитывается как:
u = es,
где u — относительный рост (значение данного параметра, например 1,25, означает ожидаемый рост стоимости проекта в 25%);
s — стандартное отклонение среднегодовой стоимости проекта;
h — интервал как часть года (к примеру,
h = 0,5, если решение по проекту принимается раз в полгода).
Относительное снижение стоимости (d) рассчитывается по формуле
d = 1 : u.
Тогда вероятность относительного роста (П), исходя из предположений о нейтральном отношении к риску, можно рассчитать как:
П = [(1 + r) — d ] : u - d.
Соответственно вероятность снижения стоимости проекта будет равна
1- П.
Таким образом, исследовав биноминальную модель можно сказать о том, что эта модель имеет важное значение при анализе инвестиционного проекта. С помощью нее можно рассчитать стоимость опциона, зная цену актива и предположить как будет расти цена инструмента в зависимости от цены его актива.
Если бы мы исследовали случай с несколькими периодами, портфель (акции, облигации и опционы) нужно было бы скорректировать: в нем должно быть столько ценных бумаг каждого вида, чтобы портфель всегда был хеджированным. Если периоды времени сокращаются и операции совершаются непрерывно, то мы приходим к модели оценки опционов Блэка— Шоулса. Модель Блэка—Шоулса не противоречит биномиальной модели, описанной в этом разделе, если предположить, что операции совершаются непрерывно и в очень короткие периоды. Оценка стоимости опционов с помощью биномиального метода при достаточно большом количестве дат принятия решений на протяжении года будет близка к значению, полученному с использованием модели Блэка—Шоулза.
2.3 Модель Блэка – ШоулсаМодель ценообразования опционов Блэка-Шоулза (Black-Scholes Option Pricing Model, OPM), которая оценивает call-опционы, была разработана в 1973 году, когда уже начался период быстрого роста опционной торговли. Данная модель получила широкое распространение на практике и, помимо всего прочего, может также использоваться для оценки всех производных бумаг, включая конвертируемые ценные бумаги, и даже для оценки собственного капитала финансово зависимых фирм.
Чтобы вывести свою модель ценообразования опционов, Блэк и Шоулз сделали следующие предположения:
1. По базисному активу колл опциона дивиденды не выплачиваются в течение всего срока действия опциона.
2. Нет транзакционных затрат, связанных с покупкой или продажей акции или опциона.
3. Краткосрочная безрисковая процентная ставка известна и является постоянной в течение всего срока действия опциона.
4. Любой покупатель ценной бумаги может получать ссуды по краткосрочной безрисковой ставке для оплаты любой части ее цены.
5. Короткая продажа разрешается без ограничений, и при этом продавец получит немедленно всю наличную сумму за проданную без покрытия ценную бумагу по сегодняшней цене.
6. Колл опцион может быть исполнен только в момент истечения опциона.
7. Торговля ценными бумагами ведется непрерывно, и цена акции движется непрерывно и случайным образом.
Современное управление рисками, применяемое в страховании, торговле на фондовом рынке и инвестировании, основывается на возможности использовать математические методы для предсказания будущего. Конечно, не со 100%-ной вероятностью, но достаточно точно для того, чтобы принять взвешенное инвестиционное решение. Основополагающий принцип работы на финансовых рынках состоит в следующем: чем больший риск вы готовы на себя принять, тем на большее вознаграждение вы вправе рассчитывать. Использование математики никогда не сможет полностью элиминировать риск, но может помочь правильно оценить степень принимаемого на себя риска и решить вопрос о справедливом вознаграждении.
Основная привлекательность опционов для покупателя объясняется тем, что ему заранее известен максимально возможный размер убытков - это величина премии, уплаченной за опцион, тогда как потенциальная прибыль теоретически неограниченна - в случае значительного роста цены базовых акций в период действия опциона, покупатель может рассчитывать на высокую прибыль. Особенно привлекательны опционы на акции, рынок которых отличается резкими и сильными ценовыми колебаниями, например, акции компаний, производящих компьютерное оборудование и программное обеспечение. Многие нынешние миллионеры из Силиконовой долины заработали свое состояние в результате того, что реализовали полученные как часть зарплаты опционы на акции своих молодых перспективных компаний.
Формула использует четыре переменные: срок действия опциона, цена, уровень процентных ставок, степень рыночных колебаний и позволяет получить справедливую величину премии, уплачиваемой за опцион. Формула Блэка-Шоулза не только заработала, она привела к трансформации всего рынка. Когда в 1973г. открылась Чикагская биржа опционов, в первый день ее работы торговалось менее 1,000 опционов, а уже к 1995г. объем ежедневной торговли превысил 1 миллион опционов.
Расчет стоимости опциона осуществляется по формуле Блэка—Шоулза, разработанной для оценки финансовых опционов типа «колл»:
![]()
где
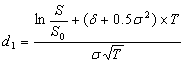
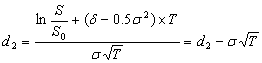
![]() -интеграл ошибок (вероятности);
-интеграл ошибок (вероятности);
S — текущая рыночная стоимость акций.
S0 – цена исполнения;
![]() - годовая безрисковая сила роста;
- годовая безрисковая сила роста;
Т – время истечения опциона в годах;
![]() - стандартное годовое отклонение цены акции
- стандартное годовое отклонение цены акции
Для расчета цены европейского опциона «пут» используется формула:
![]()
Из анализа этой формулы следует, что цена опциона тем выше, чем:
· текущая рыночная цена акции (S);
· больше времени до истечения срока опциона (Т);
· больше риск.
Следовательно, для повышения инвестиционной привлекательности проекта компаниям целесообразнее сосредоточиться на увеличении доходов, а не на снижении расходов.
Глава 3. Роль опционов в инвестиционном анализе
Похожие работы
... обсуждения руководством фирмы того, в какую сторону вообще должен развиваться бизнес данной компании. Анализ, основанный на матрице комбинирования дисконтированного денежного анализа и оценки опционов, направлен на то, чтобы создать менеджерам возможность выработать некую логику рассмотрения последствий комбинированных сигналов, которые порождаются этими двумя аналитическими подходами. 4. ...
... прироста курсовой стоимости акций, поэтому u > 1, a d - процент падения курсовой стоимости, т.е. d < 1. Рисунок 4. Динамика курса акции для одного периода биноминальной модели. Практическое значение биноминальной модели определения премии опционных контрактов Модели оценки опционов - это разновидности стандартной модели дисконтированного денежного потока с той лишь поправкой, что ...
... того, Дж. Тобин проанализировал адекватность количественных характеристик активов и портфеля, которые являются исходными данными в теории Г. Марковица. Возможно, поэтому Дж. Тобин получил Нобелевскую премию на 9 лет раньше, чем Г. Марковиц. 2. Модель оценки доходности финансовых активов. С 1964 г. появляются новые работы, открывшие следующий этап в развитии инвестиционной теории, связанный с ...
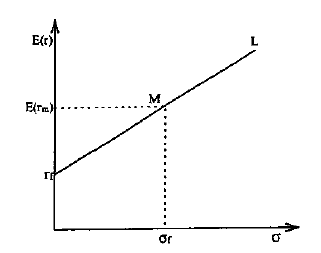
... Однако в следующие моменты должно возникнуть движение доходности актива к точке равновесного уровня. Если актив переоценен рынком, уровень его доходности ниже чем активов с аналогичной характеристикой риска, если недооценен, то выше. Показатель, который говорит о величине переоценки или недооценки актива рынком, называется альфой. Альфа представляет собой разность между действительной ожидаемой ...

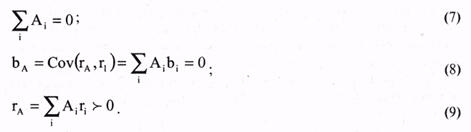
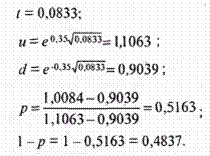
0 комментариев