Практическая работа № 2
по дисциплине "Математика"
для студентов очно – заочной формы обучения
Тема: Нахождение матрицы, обратной данной. Решение матричных уравнений. Решение системы линейных алгебраических уравнений по правилу Крамера.
Цель: Научиться находить матрицу, обратную данной., решать матричные уравнения. Научиться вычислять определители, определять совместность системы и находить решения системы линейных алгебраических уравнений по правилу Крамера.
Перечень необходимых сведений из теории:
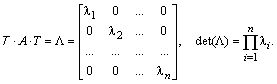
Определитель матрицы. Вычисление определителя матрицы по правилам треугольника. Алгебраические дополнения элементов матрицы. Матрица, обратная к данной.4. Системы линейных алгебраических уравнений.
5. Формулы Крамера для решения системы линейных алгебраических уравнений.
Образец выполнения задания:
Задание 1: Найдите матрицу, обратную к данной матрице
Решение:
По правилу треугольника вычислим определитель матрицы, т.к. 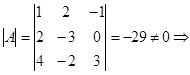 существует матрица, обратная данной.
существует матрица, обратная данной.
Вычислим алгебраические дополнения к элементам матрицы А:
|
|
|
Подставим найденные алгебраические дополнения и определитель матрицы в формулу (7) и получим: 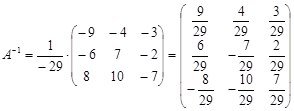
Проверку выполните самостоятельно. (![]() )
)
Ответ: 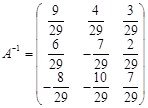
Задание 2: Решите матричное уравнение. 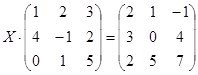
Решение: ![]() следовательно, можно решить через обратную матрицу.
следовательно, можно решить через обратную матрицу.
Найдём матрицу, обратную к А аналогично заданию №1: 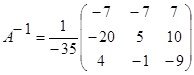 ,
, ![]() следовательно,
следовательно, 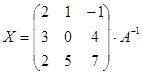
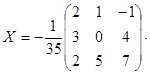
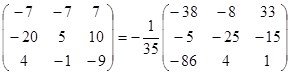
Проверка: 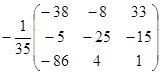
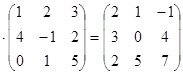
Ответ: 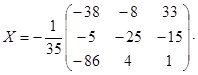
Задание 3: Решите систему линейных алгебраических уравнений по правилу Крамера: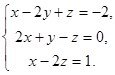
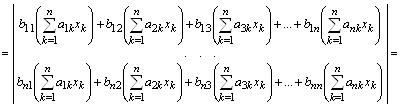
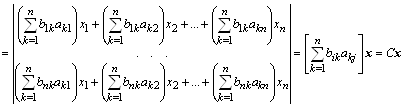
Решение: Составим определить матрицы, составленный из соответствующих коэффициентов при неизвестных:  . Вычислим определитель данной матрицы по правилу треугольников:
. Вычислим определитель данной матрицы по правилу треугольников:
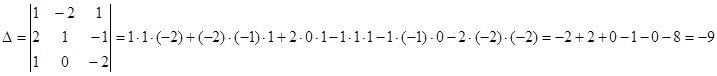
Т.К. ![]() , следовательно, система совместна и имеет единственное решение.
, следовательно, система совместна и имеет единственное решение.
Найдем определители ![]() ,подставляя столбец свободных членов
,подставляя столбец свободных членов ![]() вместо первого, второго и третьего столбцов определителя
вместо первого, второго и третьего столбцов определителя ![]() соответственно:
соответственно:
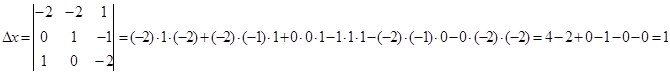

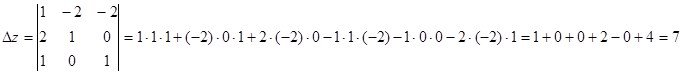
Отсюда получим решение системы линейных алгебраических уравнений:
![]() .
.
Проверку выполним, подставляя найденные значения переменных в систему уравнений (выполните самостоятельно).
Ответ: ![]()
Задания для выполнения в аудитории
Задание 1: Найдите матрицу, обратную к матрице 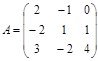 . Выполните проверку.
. Выполните проверку.
Задание 2: Решите матричное уравнение ![]() , где
, где ![]()
Задание 3: Даны системы линейных алгебраических уравнений
а) 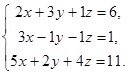 b)
b) 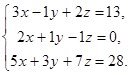
Решите системы линейных алгебраических уравнений по формулам Крамера и выполните проверку.
Задания для самостоятельного выполнения
Задание 1: Найдите матрицу, обратную к матрице 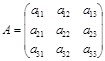 . Выполните проверку.
. Выполните проверку.
Задание 2: Решите матричное уравнение: чётные варианты: ![]() нечётные варианты:
нечётные варианты:
![]() , где
, где ![]()
![]()
Задание 3: Дана система линейных алгебраических уравнений 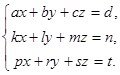 .
.
Решите систему линейных алгебраических уравнений по формулам Крамера и выполните проверку.
Исходные данные по вариантам. (задание 1,2)
|
№ вар. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
-3 |
2 |
9 |
2 |
5 |
-3 |
4 |
5 |
2 |
3 |
-1 |
6 |
3 |
-1 |
-1 |
1 |
5 |
|
2 |
3 |
4 |
2 |
8 |
2 |
-4 |
-3 |
-1 |
1 |
3 |
-1 |
2 |
-3 |
2 |
1 |
-1 |
0 |
5 |
|
3 |
1 |
2 |
3 |
5 |
4 |
5 |
6 |
8 |
7 |
3 |
-1 |
2 |
-1 |
7 |
0 |
1 |
2 |
-1 |
|
4 |
2 |
-3 |
1 |
-7 |
1 |
2 |
-3 |
4 |
-1 |
1 |
3 |
-1 |
-3 |
5 |
-1 |
4 |
5 |
3 |
|
5 |
1 |
2 |
3 |
3 |
2 |
6 |
4 |
6 |
3 |
2 |
-1 |
4 |
-7 |
7 |
3 |
-1 |
3 |
5 |
|
6 |
1 |
2 |
3 |
8 |
4 |
5 |
6 |
9 |
7 |
2 |
3 |
-4 |
-1 |
3 |
-1 |
2 |
2 |
4 |
|
7 |
1 |
2 |
3 |
4 |
2 |
6 |
4 |
-6 |
3 |
4 |
4 |
-3 |
7 |
3 |
-1 |
2 |
7 |
5 |
|
8 |
3 |
2 |
1 |
-8 |
2 |
3 |
1 |
-3 |
2 |
3 |
-2 |
1 |
-1 |
1 |
5 |
-2 |
-1 |
2 |
|
9 |
-3 |
4 |
1 |
7 |
2 |
1 |
-1 |
0 |
-2 |
5 |
-3 |
4 |
-1 |
2 |
-1 |
-2 |
-6 |
3 |
|
10 |
1 |
2 |
-3 |
-3 |
-2 |
6 |
9 |
-1 |
-4 |
5 |
-3 |
4 |
6 |
-2 |
-1 |
-1 |
0 |
1 |
Исходные данные по вариантам (задание 3)
|
№ вар. |
a |
b |
c |
d |
k |
l |
m |
n |
p |
r |
s |
t |
|
1 |
4 |
-3 |
2 |
9 |
2 |
5 |
-3 |
4 |
5 |
6 |
-2 |
18 |
|
2 |
3 |
4 |
2 |
8 |
2 |
-4 |
-3 |
-1 |
1 |
5 |
1 |
0 |
|
3 |
1 |
2 |
3 |
5 |
4 |
5 |
6 |
8 |
7 |
8 |
0 |
2 |
|
4 |
2 |
-3 |
1 |
-7 |
1 |
2 |
-3 |
14 |
-1 |
-1 |
5 |
-18 |
|
5 |
1 |
2 |
3 |
3 |
2 |
6 |
4 |
6 |
3 |
10 |
8 |
21 |
|
6 |
1 |
2 |
3 |
8 |
4 |
5 |
6 |
19 |
7 |
8 |
0 |
1 |
|
7 |
1 |
2 |
3 |
4 |
2 |
6 |
4 |
-6 |
3 |
10 |
8 |
-8 |
|
8 |
3 |
2 |
1 |
-8 |
2 |
3 |
1 |
-3 |
2 |
1 |
3 |
-1 |
|
9 |
-3 |
4 |
1 |
17 |
2 |
1 |
-1 |
0 |
-2 |
3 |
5 |
8 |
|
10 |
1 |
2 |
-3 |
-3 |
-2 |
6 |
9 |
-11 |
-4 |
-3 |
8 |
-2 |
В результате выполнения практической работы студент должен:
знать:
- определение обратной матрицы;
- алгоритм решения систем линейных алгебраических уравнений по формулам Крамера;
-
уметь:
- находить обратную матрицу;
- решать матричные уравнения.
- вычислять определитель матрицы по правилу треугольников;
- решать системы линейных алгебраических уравнений по формулам Крамера.
Похожие материалы
... его за прямые скобки. Оставшиеся коэффициенты упорядочены, как в матрице . Теперь для представления исходной системы уравнений в виде несложно определить векторно-матричную операцию , результатом которой является вектор с i-той компонентой, равной . Аксиоматическое построение линейной (векторной) алгебры с рассмотренными базовыми операциями позволило установить важные и полезные свойства, как ...
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
... лежащие на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит ...
... должны быть прямоугольными. 5. Полиномы По степени применимости, по разнообразию и качеству соответствующих команд скалярные полиномы – следующие за матрицами математические объекты в MATLAB'е. Полином p(x)=anxn+an-1xn-1+...+a0 задается вектором-строкой p из чисел an, an-1, ... , a0, т.е. коэффициентами, расположенными в порядке убывания показателя степени. Его степень n задавать не ...

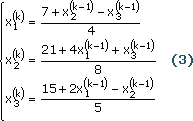

0 комментариев