Алгоритм решения однородных уравнений больших степеней, n>2.

©

Алгоритм решения однородных уравнений больших степеней, n>2.

Январь 2017г.

Начнём с кубического уравнения, -

Вспомним азы, -

- куб суммы двух чисел, (КС),

- куб разности двух чисел, (КР).

Этих знаний хватит, начнём решать примеры.

(1)

Выделим из членов уравнения (1) КР, -

(2)

Вначале интерес будут представлять подчёркнутые члены, -

(3)

Один корень нашли, - Если полученное значение подставить в уравнение (1), получим 0=0. Займёмся в уравнении (3) сомножителем в квадратных скобках, -

Заметим следующее, - в нашем случае коэффициент при в уравнении (2) по модуле меньше коэффициента при из уравнения (1), т.е. Равенство тоже возможно. Рассмотрим следующий пример, -

(4)

Выделим КС, -

(5)

(6)

В уравнении (6) для сомножителя требуется заниматься подбором из численных значений

Наше решение будет

Продолжение напрашивается следующее, -

(7)

Это неверный ход. Убедимся в этом. Для этого уравнение (7) дорешаем до конца.

Корень - это совпадение, а не удовлетворяет уравнению (4). Правильно надо поступать так, - либо уравнение (5) решать по формулам Кардано, либо уравнение (4) делить на Сделаем это, -

		,

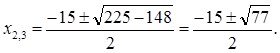
Решим следующий пример, -

(8)

До этого примеры были с Первое желание на уровне инстинкта – сделать уравнение (8) приведённым. Это делать не обязательно, хотя и ошибкой не является. Наличие в уравнении подразумевает присутствие в уравнении дробных корней. Решать будем по аналогии с предыдущими примерами, но вначале умножим все члены уравнения (8) на число четыре, -

Выделим из последнего уравнения КР и ориентироваться будем на свободный член, на число

Требуется подбор для сомножителя из чисел, -

По сравнению с исходным уравнением (8) подбор утомителен, ибо вариантов больше. Пусть нашли Чтобы найти дробные корни сделаем следующее, -

		,

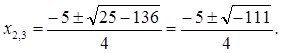
Возьмём уравнение с неполным набором членов, -

(9)

В уравнении (9) нет члена Нам хватит свободного члена

(10)

Окончательно имеем

Другие значения можно искать либо из уравнения (9) после его деления на либо из уравнения, - Это закономерность, - если справа в уравнении, типа (10), стоит нуль, тогда выражение в квадратных скобках можно приравнивать к нулю.

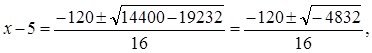
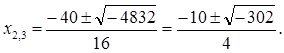
Закрепим результат, решим очередной пример, -

(11)

Умножим все члены уравнения (11) на число двенадцать, -

Подбор для сомножителя будет из чисел, -

При имеем

		,

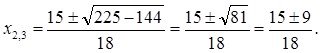
Уравнение (11) приведено в качестве иллюстрации возможностей данного метода в поисках дробных корней, когда подбор по свободному члену однородного уравнения «» затруднителен.

Разберём решение однородных уравнений четвёртой степени.

(12)

Потребуется формула, -

Далее по трафарету, как и с кубическими уравнениями. Коэффициент при равен «-15». Ближайшая к нему величина по модулю, -

- один корень нашли.

Сомножитель в квадратных скобках приравниваем к нулю, т.к. в уравнении справа стоит нуль –

Раскроем скобки, -

(13)

Выделим в уравнении (13) КР, -

(14)

Уравнение (14) можно бы и через уравнение Кардано пропустить, но пойдём своим путём, -

Подбором нашли, -

Уравнение (13) делим на «», -

		,

Имеем

Окончательно, -

Для закрепления полученных навыков решим следующий пример, -

(15)

Коэффициент при разложим на простые сомножители, -

Чтобы получить четвёртую степень коэффициента при требуется число 35721 умножить на Имеем, -

Численные значения в уравнении (15) умножим на

(16)

Начнём выделять в уравнении (16) четвёртую степень разности двух чисел, -

(17)

В уравнении (17) выполнено условие

(18)

В последнем уравнении из подчёркнутых членов выделим куб разности двух членов, а конкретно, -

Разложим коэффициент при на простые сомножители

Число 916839 умножим на число три, -

Численные значения уравнения (18) умножим на число три, -

(19)

В уравнении (19) из подчёркнутых членов именно сейчас и можно выделить куб разности двух чисел, - после предварительной работы с коэффициентом при

Из подчёркнутых членов выделим квадрат разности двух чисел, - -

Из подчёркнутых членов выделим, - -

Разложим свободный член в правой части последнего уравнения на простые сомножители, -

Подбором установлено, -

Проверка удовлетворяет уравнению (15).

Избавим уравнение (15) от корня -

(20)

В уравнении (20) разложим коэффициент при -

Число 11907 умножим на «21»

Численные значения уравнения (20) умножим на «21», -

(21)

Из уравнения выделим куб разности двух чисел

(22)

Разложим коэффициент при на множители, -

Число 6615 умножим на число «21», -

Члены уравнения (22) умножим на число «21», -

Разложим число 1497475 на множители, -

Подбором установили, -

Проверка удовлетворяет уравнению (15).

В уравнении (20) избавимся от корня

Решим квадратное уравнение, -

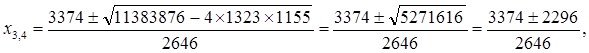
Значения и удовлетворяют уравнению (15).

Подведём предварительные итоги.

Представленный алгоритм не изящен, ибо требуется подбор.

Но есть и плюсы. Если посмотреть на пример (15), то в первоначальном его виде подбор решений из свободного члена «64350» проблематичен. Недостатком алгоритма очевидно является невозможность нахождения решений в уравнениях четвёртой степени, если все четыре корня являются мнимыми.

В заключении разберём следующий момент. В представленном алгоритме накладывалось ограничение на величину коэффициента при втором члене выделяемого многочлена. Это судя по практике лишнее. Возьмём для рассмотрения пример (1), -

Из уравнения выделим КР, и пусть коэффициент у выделяемого КР при будет

Подбором установлено, -

В рассмотренном примере было Усилим неравенство, - возьмём

В последнем примере не пришлось заниматься подбором. Это интересный результат. Попробуем решить пример (8) также ещё одним вариантом. При первоначальном решении был очень большой выбор для подбора. Посмотрим, что будет сейчас.

Разложи свободный член 118 на простые множители, -

Варианты для подбора сомножителя - что значительно меньше, чем выше по тексту.

Правильным подбором будет

Как видим вариантов для решения однородных уравнений сочинить можно много. Кому какой понравится, - на любителя.

Решения однородных уравнений при рассматривать не будем. Принципиально нового там ничего нет. Плюсом данной статьи является возможность находить дробные значения корней уравнений. В идеале, требуется вывод формул для решения однородных уравнений со степенью Кардано не в счёт. Утверждение, что таких уравнений не существует при сомнительно.

Белотелов В.А.