Навигация
ПРЕОБРАЗОВАНИЕ СИСТЕМЫ ОТСЧЕТА МИНКОВСКОГО
89841
знак
0
таблиц
6
изображений
4. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ ОТСЧЕТА МИНКОВСКОГО
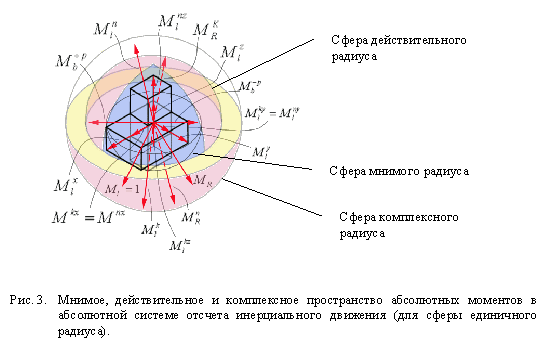
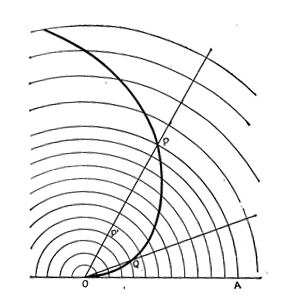
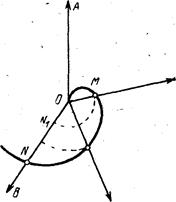
С учетом вышесказанного, преобразование ИСО СТО Минковского, с целью снятия противоречий, предполагает две главных процедуры (рис.1, рис.2):
4.1. Мнимый поворот координатных осей пространства-времени Минковского.
А) Мнимый поворот х-подобной оси х (ИСО СТО) на 
до совмещения с отрицательной полуосью времени -t (конус прошлого) и превращением ее в отрицательную мнимую величину -iх, противонаправленную времени t (Г.Корн, Т.Корн. Справочник по математике, -М.: Наука, 1973, с.31-33). Закон сохранения (для интервала массы покоя) приобретает следующее выражение:
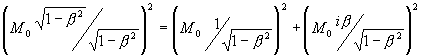3)
Поворот не изменил отношений в формуле 2). Пространственный вектор приобрел отрицательный знак относительно положительного вектора и заменил суммой разность между двумя квадратами относительных интервалов ИСО СТО, но при этом, вошедшая в выражение импульса мнимая единица, вернула нас вновь к разности квадратов интервалов.
Б) Этому повороту соответствует аналогичный поворот и совмещение -ct и ct (далее
) и, кроме того, общий поворот совмещенных осей () на 
в положение, перпендикулярное совмещенным осям (T,iХ), т.е в положение, занимаемое осью пространства ИСО СТО :
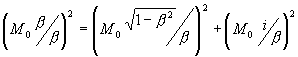4)
Относительный интервал энергии (
) получил зеркальную, x-подобную форму, относительный интервал импульса (Мо* 1/), наоборот, t-подобную форму, абсолютный интервал Мо* /
– x-подобную форму. Взятые относительно светоподобного интервала = 1/1, уравнения приобретают абсолютно идентичную количественную форму с зеркальной метрикой: свойство абсолютного интервала приобретает энергия (x-подобная и t-подобная), абсолютные интервалы в уравнениях 3) и 4) приобретают роль относительных импульсов. Абсолютные, комплексные: t-подобный 
и x-подобный 
интервалы энергии связывают в псевдоевклидовой геометрии Минковского пары относительных осевых противоположно направленных импульсов, при этом :
5)
6)
Природа псевдоевклидовой метрики связана с осевым (положительным и отрицательным) направлением относительных импульсов. Абсолютный интервал - комплексная величина. Квадрат абсолютного интервала энергии - полная энергия оси, равная разности квадратов импульсов (при скоростях и i
). С учетом мнимой величины, не исключена возможность того, что разность квадратов импульсов в правой части равенства - это разность кинетической и потенциальной энергий. Характерной особенностью уравнений, кроме их зеркальной симметрии, является то, что при действительном и мнимом импульсах, интервал энергии выступает как абсолютный, комплексный, скалярный интервал, но в случае, если мнимый импульс приобретает действительную форму, комплексная энергия приобретает действительную форму и при = =, (при
с), ее интервал равен нулю. В ИСО СТО условие равенства относительных интервалов выполняется при =1 (при скорости света). Второй особенностью является то, что из уравнений сохранения (в связи с переходом к 
= 1/1) , устранены бесконечные величины (уравнения 5), 6)). Кроме того, x-подобные (так же как и t-подобные) полуоси связаны теоремой Пифагора в Евклидовой метрике. При всех значениях разрешенных скоростей осевые и 
взаимно ортогональны.
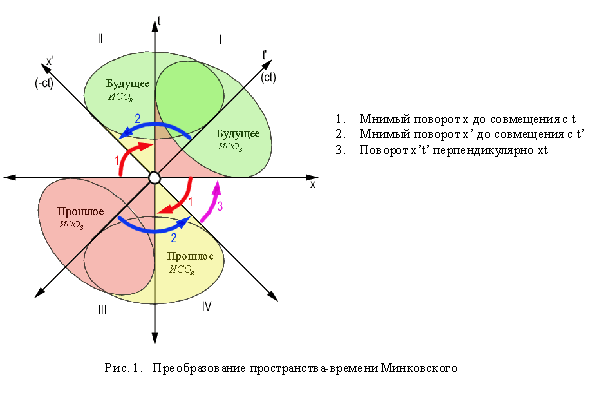
4.2. Подвижный трехгранник Френе и пространство кручений. Поскольку вновь образованная, за счет зеркальной симметрии, ИСО уже не может быть связана с поступательным движением (обе ИСО имеют единый центр, и следовательно движение может быть связано с изменением направления скорости, в условиях отсутствия трансляций), поскольку при изменении скоростей координатное пространство не подвержено преобразованиям с кручениями осей подобно ИСО СТО, она может рассматриваться только как вращательная (торсионная) система отсчета, а движение в ней (расширение или сокращение), может рассматриваться как функция изменения состояния пробной массы (объема, плотности). В связи с вышесказанным, ИСО может интерпретироваться как комплексная форма соединения мнимого и действительного “подвижных” трехгранников Френе для случая кручений по направлениям базисных (нормального, касательного, бинормального) векторов. При этом, плоскость векторов нормального и касательного моментов, соответствующая относительным импульсам в и, представляется как соприкасающаяся плоскость, а третий вектор, ортогональный двум указанным – бинормаль, равен векторному произведению нормального и касательного векторов (Г.Корн, Т.Корн. Справочник по математике. – М.: Наука, 1973г., с.521-524).
Характерно, что нормаль (или главная нормаль), касательная и бинормаль – компоненты базисных векторов трехгранника Френе, связаны с кривизной и кручением пространства и лежат в основе тензорного определения кривизны пространства (например, тензоры Риччи второго ранга), примененного А.Эйнштейном в ОТО. В связи с комплексной формой выражения законов сохранения, ИСО представлена тремя (действительным, мнимым и комплексным) трехгранниками Френе. Результатом зеркальной симметрии двух трехгранников, подвижных в противоположных направлениях, является статичная система отсчета, в которой отсутствуют трансляционные координаты (т.е. отсутствует пространство-время). Потеря пространственно-временной определенности – цена перехода к шестимерному пространству кручений. В условиях зеркальной симметрии нормального и касательного базисных векторов, векторное произведение нормальной скорости (мнимой или действительной) на касательную (мнимую или действительную) в инерциальной системе отсчета будет иметь форму квадратов относительных скоростей соответственно 
= 11, 
,.
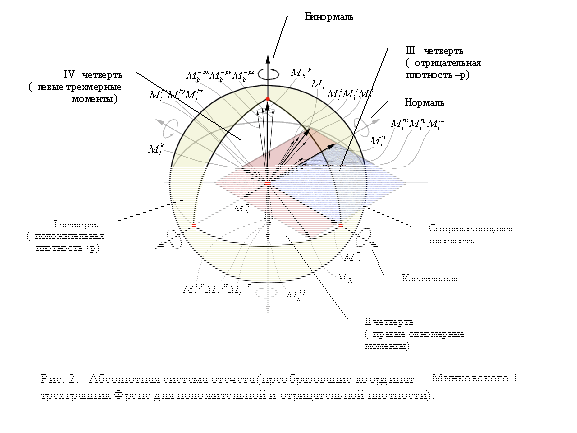
Таким образом ИСО связана с кручениями, где: 1, и - относительные угловые скорости ; = 11, , - бинормальные (квадратичные) скорости. Импульсы и энергии в законах сохранения, соответственно, являются моментами (инерции) энергий и импульсов. Поскольку в полученной системе отсчета состояние покоя связано с = = или 0,707… скорости света, (при
, связанной с массами положительной плотности и при, связанной с массами отрицательной плотности), состояние покоя результирующей системы будет характеризоваться нулевой плотностью покоя. (+p) + (-p) = 0, а сама система отсчета может рассматриваться как абсолютная система отсчета движения изолированной физической системы. Различие в метрике отдельных элементов системы отсчета отражает не отношения пространства и времени, а отношения между 3-мерными и 1-мерными элементами пространства скоростей (в частности нормальные и касательные скорости).
4.3. Уравнения законов сохранения в абсолютной системе отсчета. Геометрия преобразованной системы включает следующие основные законы сохранения (при следующих физических величинах):
- момент инерции (эквивалентный массе покоя),
1 - абсолютный интервал относительной угловой скорости 1 = с/с
- относительный интервал относительной угловой скорости = v/c, может, например, рассматриваться как угловая скорость положительной массы, как векторное разложение квадратичной бинормальной скорости на равные между собой нормальную и касательную скорости инерции положительной массы
- относительный интервал относительной угловой скорости может, рассматриваться как угловая скорость отрицательной массы, как векторное разложение квадратичной бинормальной скорости на равные между собою нормальную и касательную скорости инерции отрицательной массы
- угол между скоростью и скоростью 1
;
;; 
-общая форма уравнения скоростей
Ниже, в принципиальной форме, приведены основные уравнения абсолютных и относительных интервалов моментов (в примерном виде по модулю), без учета изменения направлений векторов скоростей и мнимых характеристик крутящих моментов. Уравнения легко переводятся в чисто геометрическую форму для единичной сферы (при =1).
А) Относительные (нормальные и касательные правовинтовые и левовинтовые
) моменты в соприкасающейся плоскости подвижного трехгранника Френе (всего - 4):
1а) 
- нормальный x-подобный интервал левого момента инерции
2а) 
- касательный x-подобный интервал левого момента инерции
3а) 
- нормальный t-подобный интервал правого момента инерции
4а) 
- касательный t-подобный интервал правого момента инерции
Б) Абсолютные (нормальные и касательные правовинтовые
и левовинтовые) интервалы моментов инерции в соприкасающейся плоскости подвижного трехгранника Френе (всего – 4):
1б) 
- абсолютный x-подобный интервал (4-я четверть)
2b) 
- абсолютный t-подобный интервал правых (2-я четверть)
3b) 
- абсолютный осевой xt-подобный интервал нормальных (,) -моментов
4b) 
- абсолютный осевой xt-подобный интервал касательных (,) -моментов
В) Бинормальные 3х мерные моменты инерции (,) для (+P) и (-P) плотности на бинормали подвижного трехгранника Френе:
1в) 
- относительный интервал бинормального момента инерции -P плотности
2в) 
-относительный интервал бинормального момента инерции +P плотности
3в) 
абсолютный бинормальный момент инерции +P плотности
нормальный и касательный моменты инерции в соприкасающейся плоскости могут рассматриваться как производные (корни) от положительных и отрицательных бинормальных моментов: 
и, соответственно, могут принимать значения:;
;;
4в) 
- относительный векторный бинормальный RL-момент инерции
где
= - угол между и продолжением
5в) 
- относительный скалярный бинормальный RL-момент инерции
где = - угол между и продолжением
Кроме того, поскольку бинормальный момент является произведением нормального и касательного векторов, один из которых 3-мерный, бинормальный вектор представляется в его трехмерной проекции.
Г) Нормальное (действительное), касательное (мнимое) и бинормальное (комплексное) пространства 3-мерных x-подобных моментов.
1г) (
, ,
) – касательный x-подобный момент и его ХУZ-проекции
2г) 
(
) - нормальный x-подобный момент и его ХУZ -проекции
3г) (
)- комплексный (результирующий) x-подобный момент и его ХУZ- проекции.
4г)
; 5г); 6г)
;
7г)
; 8г)
9г)
, при
10г)
, при
11г)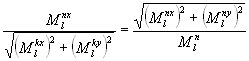
; 12г)
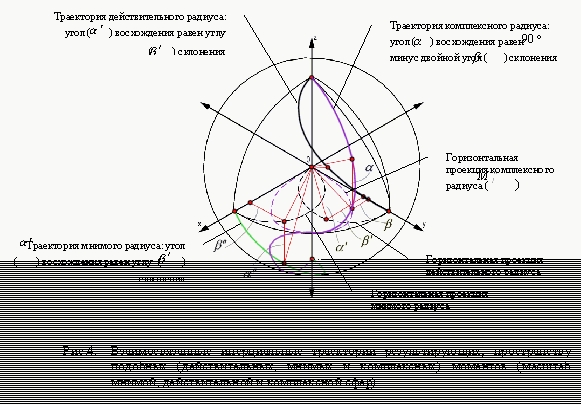
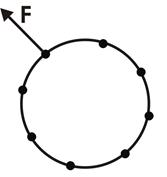
Уравнениям x-подобных моментов инерциального движения в системе декартовых координат, соответствуют инвариантные уравнения в полярных координатах (угол восхождения радиуса равен углу склонения, угол восхождения радиуса равен минус удвоенный угол склонения), отражающие специфику симметрии геометрии комплексного пространства (рис.4). При всех значениях скоростей, для пространственных модулей характерны среднепропорциональные отношения (11г, 12г).
Приведенные уравнения (а всего с учетом x-подобных, t-подобных, xt-подобных моментов, интервалов и результирующих моментов в их более 50: -13 осевых на нормали, - 13 осевых на касательной, - 13 RL-винтовых, между x-подобной и t-подобной четвертями, - 16 осевых xt-подобных на бинормали) демонстрирует богатство отношений закона сохранения движения, определяя геометрию инерциального движения на всем (
) диапазоне скоростей. С учетом различных, возможных вариаций мнимых и действительных моментов, общее количество уравнений сохранения значительно больше. Подобное многообразие мнимых, действительных и комплексных отношений инерциального движения проявляется, вероятно, не только на “виртуальном” уровне микро-материи (в мире микрочастиц), но и на других, более сложных макро- и мега- уровнях организации материи.
Переход из ИСО СТО в абсолютную систему отсчета можно проиллюстрировать следующим образом. Внешний наблюдатель явлений, происходящих в ИСО, неудовлетворенный тем, что гравитационные эффекты не обеспечивают, неискаженных кривизной пространства-времени результатов наблюдений пробной массы, обнаруживает, что в наблюдаемой ИСО, кроме базового координатного пространства (), существует инвариантная, но зеркальная система координат (относительно). Переход в нее связан с зеркальными преобразованиями, заменой с 
(расширяющаяся) на 
(сокращающаяся). Заняв место в новой, он обнаруживает; что центры обоих ИСО, совпадают; что изменение скорости не связано, ни с перемещениями относительно центра, ни с преобразованиями координатного пространства; что он всегда находится, в общем, для обоих ИСО центре, но в зеркальной системе, привычное для него расширение массы, превратилось в сокращение. Зная, что относительные связаны между собой абсолютной скоростью света, он обнаруживает еще одну, третью, , (. = 1/1 = с/с), которая ни расширяется, ни сокращается, а всегда находится в состоянии покоя. Относительно третьей ИСО, движение исследуемой массы - суть взаимосвязанные процессы сжатия и расширения (относительно состояния покоя =) под действием правых и левых моментов кручения, положительных и отрицательных энергий плотности
Похожие работы
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... философия (основные положения, проблемы, понятия).} 21. ФИЛОСОФИЯ ЭКЗИСТЕНЦИАЛИСТОВ. (Камю. "Миф и Сизифе. Эссе об абсурде", Сартр. "Экзистенциализм - это гуманизм"). Экзистенциализм - Философия существования. Иррационалистическая фил. Наиболее крупные представители: М. Хейдеггер, религиозный( К Ясперс, Г.Марсель, ) атеистический (Ж.П.Сартр, А.Камю), Н.Аббаньяно. В Герм э. ...
... методология исследования биологических циклов. В этой связи можно указать на работы ученого из Ставрополя профессора Гневушева В.В. В своих работах Гневушев В.В. активно использует общую теорию циклов и выходит на совершенно оригинальные и неожиданные результаты. Исследования хронобиологов не могут не использоваться в современной медицине. Процесс циклизации медицины в самом широком смысле уже ...
... и более живой. Хотя простейший из изучаемых уровней самоорганизации - это уровень диссипативных структур, образованных в самообновляющихся химических реакциях, применение этих принципов к биологическим, психологическим и социологическим явлениям нельзя назвать редукционистским мышлением. В отличие от редукционизма в механистической науке такие интерпретации основаны на фундаментальной гомологии, ...
0 комментариев