Навигация
Потоки насыщения и выбор стратегии механизма обслуживания
4. Потоки насыщения и выбор стратегии механизма обслуживания.
Обозначим через ![]() , максимально возможное число обслуженных на интервале времени
, максимально возможное число обслуженных на интервале времени ![]() требований потока
требований потока ![]() при наличии в накопителе
при наличии в накопителе ![]() бесконечной очереди. Тогда соответствующий поток насыщения
бесконечной очереди. Тогда соответствующий поток насыщения ![]() может быть описан с помощью маркированного точечного процесса
может быть описан с помощью маркированного точечного процесса![]() , где
, где ![]() метка обслуженных заявок на интервале
метка обслуженных заявок на интервале ![]() . Интерпритировать подобное описание
. Интерпритировать подобное описание ![]() можно как влияние погодных условий (состояния случайной среды) на механизм обслуживания. Более подробно этот процесс будет рассмотрен ниже. Мы не будем задавать конечномерные распределения маркированных точечных процессов
можно как влияние погодных условий (состояния случайной среды) на механизм обслуживания. Более подробно этот процесс будет рассмотрен ниже. Мы не будем задавать конечномерные распределения маркированных точечных процессов ![]() и
и ![]() поскольку при нелокальном описании входных потоков и потоков насыщения можно ограничеться некоторыми свойствами условных распределений дискретных компонент
поскольку при нелокальном описании входных потоков и потоков насыщения можно ограничеться некоторыми свойствами условных распределений дискретных компонент ![]() и
и ![]() .
.
Допустим, что величина ![]() задает на промежутке
задает на промежутке ![]() число фактически обслуженных заявок потока
число фактически обслуженных заявок потока ![]() . Для описания реального процесса обслуживания нужно при любом
. Для описания реального процесса обслуживания нужно при любом ![]() и каждом
и каждом ![]() указать зависимость
указать зависимость
![]() (4)
(4)
то есть некоторую стратегию ![]() механизма обслуживания. На выбор функции (4) естественно наложить следующие ограничения:
механизма обслуживания. На выбор функции (4) естественно наложить следующие ограничения:
![]() ;
;
![]() ;
;
Откуда получим:
![]() ; (5)
; (5)
Автомат, как правило, за промежуток времени ![]() обслуживает максимально возможное число машин
обслуживает максимально возможное число машин ![]() из потока
из потока ![]() или все поступающие и находящиеся в очереди машины этого потока, если их число меньше
или все поступающие и находящиеся в очереди машины этого потока, если их число меньше ![]() .
.
Тогда зависимость (4) будет иметь вид:
![]() (6)
(6)
Такая стратегия механизма обслуживания, учитывая (5), называется экстремальной.
5. Рекуррентные соотношения для маркированного точечного процесса обслуживания. Свойства условных распределений для дискретных компонент ![]() , соответствующих входным потокам и потокам насыщения.
, соответствующих входным потокам и потокам насыщения.
Будем описывать поведение системы маркированным точечным процессом ![]() с выделенной дискретной компонентой
с выделенной дискретной компонентой ![]() , где
, где ![]() - вектор длин очередей по потокам в момент
- вектор длин очередей по потокам в момент ![]() . Для процесса
. Для процесса ![]() основываясь на равенствах (1)-(3), имеет место следующее рекуррентное соотношение:
основываясь на равенствах (1)-(3), имеет место следующее рекуррентное соотношение:
![]() (7)
(7)
где ![]() ,
, ![]() ,
,![]() . Здесь векторное соотношение
. Здесь векторное соотношение ![]() предполагает выполнение равенств
предполагает выполнение равенств ![]() при
при ![]() . Принимая во внимание
выбранную нами экстремальную стратегию обслуживания
. Принимая во внимание
выбранную нами экстремальную стратегию обслуживания ![]() , имеем:
, имеем: ![]()
Для изучения вероятностных свойств метки ![]() остановимся на некоторых свойствах условных распределений величин
остановимся на некоторых свойствах условных распределений величин ![]() и
и ![]() . Полагаем что в этой модели при фиксированных значениях метки
. Полагаем что в этой модели при фиксированных значениях метки ![]() случайные величины
случайные величины![]() и
и ![]() независимы и их условные распределения при любом
независимы и их условные распределения при любом ![]() и при
и при ![]() удовлетворяют соотношениям:
удовлетворяют соотношениям:
![]()
![]()
![]()
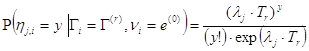 ; (8.1)
; (8.1) 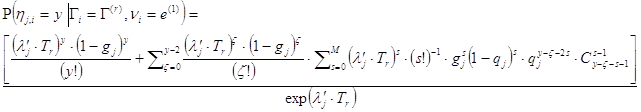
![]()
![]() (8.2)
(8.2)
![]()
![]()
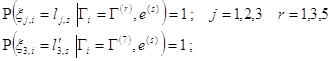 (9)
(9)
где ![]() - целая часть величины
- целая часть величины ![]()
![]() , а
, а ![]() ,
, ![]() - средняя интенсивность обслуживания заявок по потоку
- средняя интенсивность обслуживания заявок по потоку ![]() если случайная среда на интервале
если случайная среда на интервале ![]() находится в состоянии
находится в состоянии ![]() , здесь
, здесь ![]() - интенсивность пуассоновского поступления заявок по потоку
- интенсивность пуассоновского поступления заявок по потоку ![]() ,
, 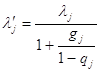 ,
, ![]() ,
, ![]() - параметры распределения Бартлетта,
- параметры распределения Бартлетта, ![]() - целая часть величины
- целая часть величины ![]() .
.
6. Марковское свойство компоненты ![]() .
.
Итак, мы определили все компоненты нашей модели: входные потоки, алгоритм управления, потоки насыщения и экстремальную стратегию механизма обслуживания. В соответствии со структурой анализируемой системы управления 3 конфликтными потоками требований, максимальный интерес представляет исследование процессов обслуживания по потокам ![]() и
и ![]() . Ключевое свойство дискретной компоненты процесса
. Ключевое свойство дискретной компоненты процесса ![]() можно сформулировать в виде следующей теоремы:
можно сформулировать в виде следующей теоремы:
Теорема: Последовательности ![]() ,
, ![]() и
и ![]() при заданном распределении вектора
при заданном распределении вектора ![]() являются марковскими.
являются марковскими.
Доказательство:
Докажем правильность утверждения для последовательности![]() . Сообразно определению, данная последовательность будет марковской, если выполнено равенство
. Сообразно определению, данная последовательность будет марковской, если выполнено равенство 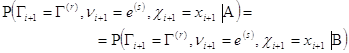
Где
![]()
![]()
Применяя формулу полной вероятности и принятые в данной модели основные свойства ее случайных элементов, получим:
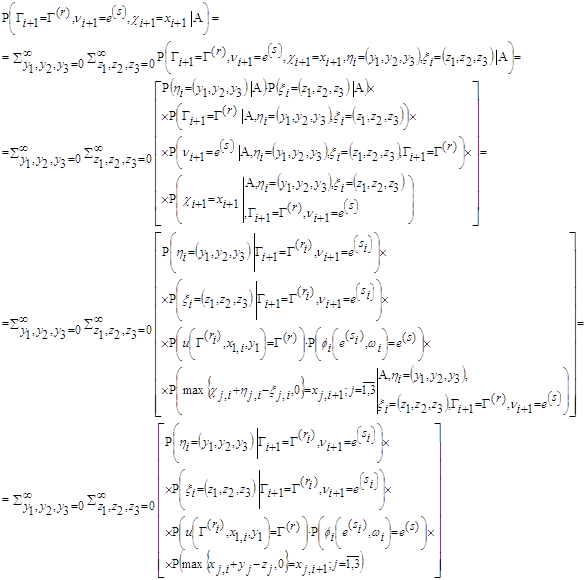
для правой части доказываемого равенства из тех же соображений получим
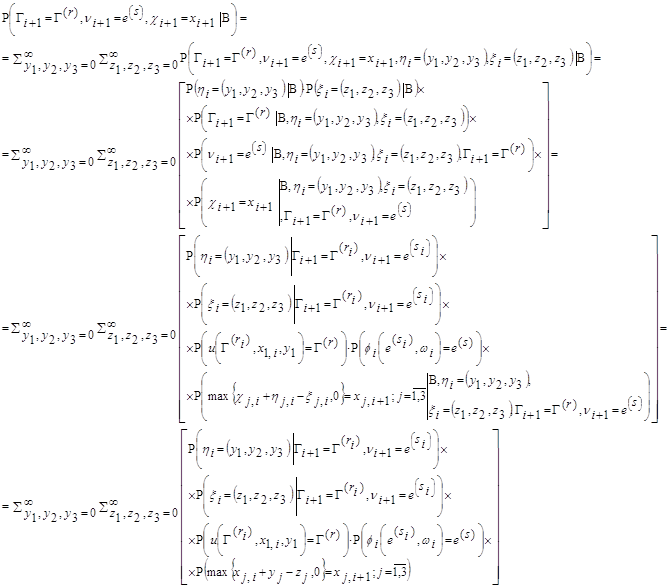
Т.е. доказываемое равенство имеет место. Стало быть, случайная последовательность ![]() образует
цепь Маркова с бесконечным счетным числом состояний.
образует
цепь Маркова с бесконечным счетным числом состояний.
Аналогично доказывается марковость последовательностей ![]() и
и ![]() .
.
7. Рекуррентные формулы для одномерных распределений дискретной компоненты маркированного точечного процесса ![]() .
.
Исследуем свойства одномерных распределений
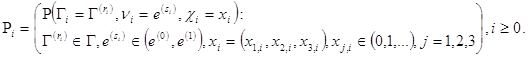
Здесь начальное распределение ![]() считается заданным. Получим рекурентные соотношения вида
считается заданным. Получим рекурентные соотношения вида ![]() , где
, где ![]() - бесконечномерная матрица переходных вероятностей за один шаг процесса
- бесконечномерная матрица переходных вероятностей за один шаг процесса ![]() . Подробно рассмотрим вероятностные свойства последовательностей
. Подробно рассмотрим вероятностные свойства последовательностей ![]() и
и ![]() . Из (7) нетрудно получить следующие, реккурентные по
. Из (7) нетрудно получить следующие, реккурентные по ![]() соотношения для этих последовательностей:
соотношения для этих последовательностей:
![]()
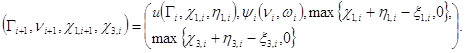
Заметим что исследование последовательностей ![]() и
и ![]() , проводятся аналогично.
, проводятся аналогично.
Введём следующие обозначения:
![]()
![]()
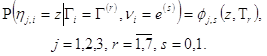
На основании доказанного свойства марковости рассматриваемых последовательностей и формулы полной вероятности можно видеть что имеют место формулы:
![]()
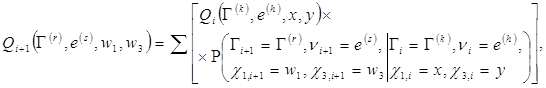 (10)
(10)
где суммирование ведётся по ![]()
Теперь вычислим условные вероятности:
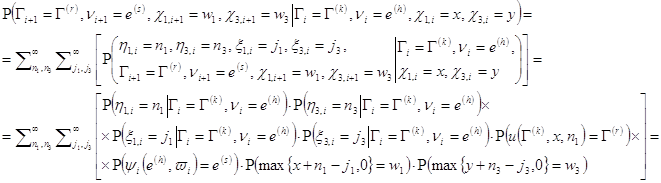
Окончательно формула (10) примет вид:
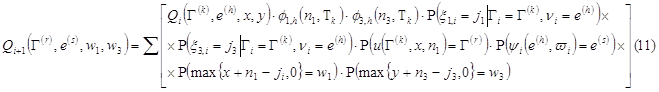 Здесь суммрование ведётся по всем точкам
Здесь суммрование ведётся по всем точкам
![]() Учитывая вид условных распределений для
Учитывая вид условных распределений для ![]() (8.1)-(9), нетрудно получить конкретный вид рекурентных формул для одномерных распределений дискретной компоненты
(8.1)-(9), нетрудно получить конкретный вид рекурентных формул для одномерных распределений дискретной компоненты ![]() . Подробно приведём только вывод формулы для вероятностей
. Подробно приведём только вывод формулы для вероятностей ![]() при
при ![]() .
.
Используя формулу (11), учитывая что при ![]() на интервалах времени
на интервалах времени ![]() ни один из потоков не обслуживается, получим для
ни один из потоков не обслуживается, получим для ![]() .
.
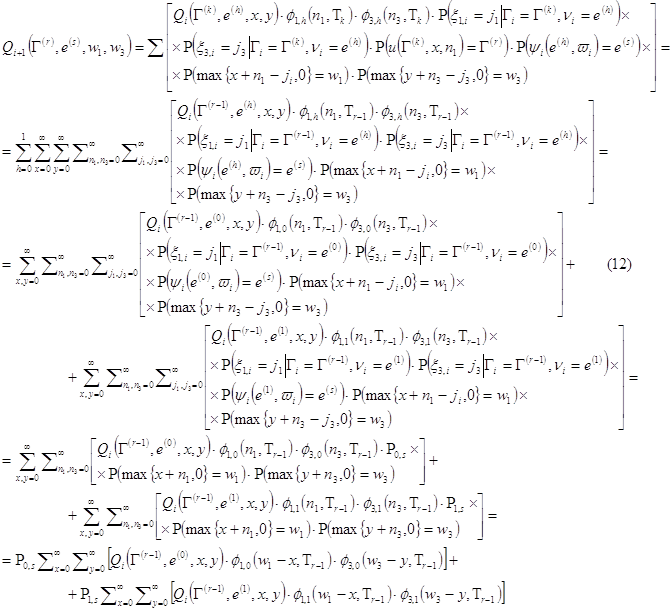 где полагаем при
где полагаем при ![]() .
.
Вероятности ![]() , образуют матрицу
, образуют матрицу
![]()
Далее через ![]() мыбудем обозначать соответственно целые части величин
мыбудем обозначать соответственно целые части величин ![]() , где
, где ![]() -интенсивность обслуживания по потоку
-интенсивность обслуживания по потоку ![]() , если случайная среда находится в состоянии
, если случайная среда находится в состоянии ![]() .
.
Поскольку при ![]() обслуживаются только требования потока
обслуживаются только требования потока ![]() ,
,
рекуррентные соотношения для вероятностей ![]() при
при![]()
![]()
![]() получаются в виде:
получаются в виде:
![]() (13)
(13)
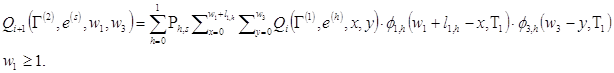 (14)
(14)
Так как при ![]() происходит обслуживание требований только по потоку
происходит обслуживание требований только по потоку ![]() , то при
, то при ![]() получим, что
получим, что ![]() при всех
при всех ![]() и
и ![]() , а при
, а при ![]() имеем:
имеем:
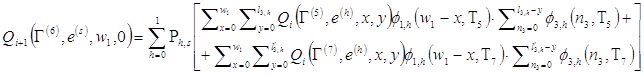 (15)
(15)
а при любых ![]() :
:
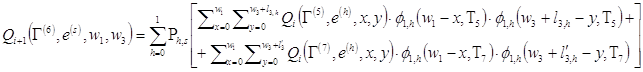 (16)
(16)
Наконец для вероятностей ![]() имеем
имеем ![]() при любом
при любом ![]() ,
, ![]() ,
, ![]() .
.
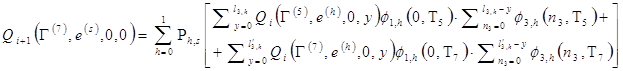 (17)
(17)
а при любых ![]() ,
, ![]() .
.
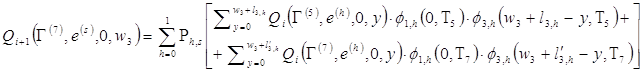 (18)
(18)
Заметим, что поскольку вероятности ![]() для
для ![]() ,
, ![]() ,
, ![]() то из (12) непосредственно следует, что
то из (12) непосредственно следует, что ![]() при всех для
при всех для ![]() ,
, ![]() ,
, ![]() .
.
Уточним теперь структуру цепи Маркова ![]() . Обозначим через
. Обозначим через ![]() . Сформулируем и докажем два вспомогательных утверждения, касающихся общей структуры цепи и асимптотического поведения распределения рассматриваемой цепи Маркова при
. Сформулируем и докажем два вспомогательных утверждения, касающихся общей структуры цепи и асимптотического поведения распределения рассматриваемой цепи Маркова при ![]() .
.
Лемма 1. Пространство ![]() состояний цепи Маркова
состояний цепи Маркова ![]() распадается на незамкнутое множество
распадается на незамкнутое множество ![]() несущественных состояний и минимально замкнутое множество
несущественных состояний и минимально замкнутое множество ![]() существенных сообщающихся непериодических состояний.
существенных сообщающихся непериодических состояний.
Доказательство. Из того, что ![]() и
и ![]() для всех
для всех ![]() , следует что случайный процесс
, следует что случайный процесс ![]() за некоторое конечное число шагов из произвольного состояния
за некоторое конечное число шагов из произвольного состояния ![]() с положительной вероятностью по цепочке
с положительной вероятностью по цепочке ![]() попадёт в состояние
попадёт в состояние ![]() . Следовательно состояние
. Следовательно состояние ![]() является существенным. Согласно теореме 3.5 из /7/ совокупность состояний цепи, сообщающихся с
является существенным. Согласно теореме 3.5 из /7/ совокупность состояний цепи, сообщающихся с ![]() также является существенным. Используя полученные нами рекурентные соотношения (12)-(18) и приведённые выше замечания нетрудно видеть, что множество
также является существенным. Используя полученные нами рекурентные соотношения (12)-(18) и приведённые выше замечания нетрудно видеть, что множество 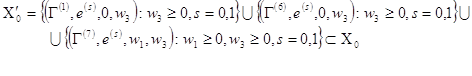
Покажем, что ![]() не содержит других состояний, кроме отмеченных. Возьмём, к примеру, состояние
не содержит других состояний, кроме отмеченных. Возьмём, к примеру, состояние ![]() где
где ![]() . Тогда по цепочке переходов
. Тогда по цепочке переходов ![]() цепь Маркова
цепь Маркова ![]() перейдёт из существенного состояния
перейдёт из существенного состояния ![]() в состояние
в состояние ![]() . Следовательно, состояние
. Следовательно, состояние ![]() является существенным и сообщающимся с
является существенным и сообщающимся с ![]() . Указанный переход возможен с положительной вероятностью, поскольку
. Указанный переход возможен с положительной вероятностью, поскольку ![]() и
и ![]() . Аналогично доказывается, что возможен переход из
. Аналогично доказывается, что возможен переход из ![]() или
или ![]() в любое другое состояние, не принадлежащие множеству
в любое другое состояние, не принадлежащие множеству ![]() . Значит
. Значит ![]() . Поскольку состояние
. Поскольку состояние ![]() достижимо из любого состояния
достижимо из любого состояния ![]() , то множество
, то множество ![]() не является замкнутым, а
не является замкнутым, а ![]() содержит единственное
замкнутое минимальное
содержит единственное
замкнутое минимальное ![]() . Из очевидного неравенства
. Из очевидного неравенства
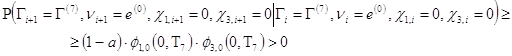
следует, что все состояния из будут непериодическими (/8/ стр. 408). Лемма доказана.
Лемма 2. При любом начальном распределении ![]() векторной цепи Маркова
векторной цепи Маркова ![]() либо для всех
либо для всех ![]() :
:
![]() и в системе не существует стационарного распределения, либо существуют пределы:
и в системе не существует стационарного распределения, либо существуют пределы:
![]() такие, что
такие, что ![]() , и всистеме существует стационарное распределение.
, и всистеме существует стационарное распределение.
Доказательство. Из структуры множества ![]() и из того, что
и из того, что ![]() следует, что векторный случайный процесс
следует, что векторный случайный процесс ![]() из произвольного состояния
из произвольного состояния ![]() с положительной вероятностью, не меньшей, чем
с положительной вероятностью, не меньшей, чем ![]() , за один шаг может достигнуть множества
, за один шаг может достигнуть множества ![]() . Обозначим через
. Обозначим через ![]() вероятность того, что рассматриваемая цепь Маркова исходя из произвольного несущественного состояния
вероятность того, что рассматриваемая цепь Маркова исходя из произвольного несущественного состояния ![]() когда-либо достигнет некоторого существенного состояния из
когда-либо достигнет некоторого существенного состояния из ![]() . Известно, что величины
. Известно, что величины ![]()
![]() , являются решениями системы уравнений вида (8.6), приведённой в /8/ на стр. 392. Тогда, в силу неравенства
, являются решениями системы уравнений вида (8.6), приведённой в /8/ на стр. 392. Тогда, в силу неравенства ![]() и леммы 1, эта система является вполне регулярной и имеет ограниченное решение
и леммы 1, эта система является вполне регулярной и имеет ограниченное решение ![]() ,
, ![]() . В этом можно убедиться непосредсвенной подстановкой. По теореме 11 из /9/ это решение будет единственным. Отсюда на основании эргодической теоремы в главе 15 из /8/ получим утверждение доказываемой леммы.
. В этом можно убедиться непосредсвенной подстановкой. По теореме 11 из /9/ это решение будет единственным. Отсюда на основании эргодической теоремы в главе 15 из /8/ получим утверждение доказываемой леммы.
Итак, ассимптотическое поведение одномерного распределения ![]() случайного векторного процесса
случайного векторного процесса ![]() при
при ![]() не зависит от начального распределения
не зависит от начального распределения ![]() .
.
Заключение.
В конце этой (весьма краткой) работы хочется подвести итог того, что нами было уже сделано:
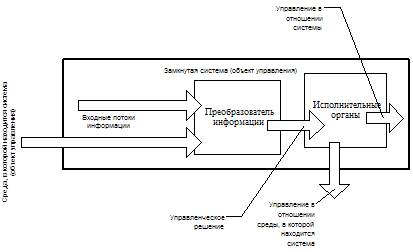
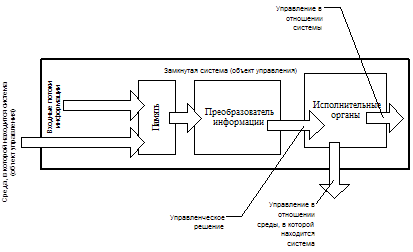
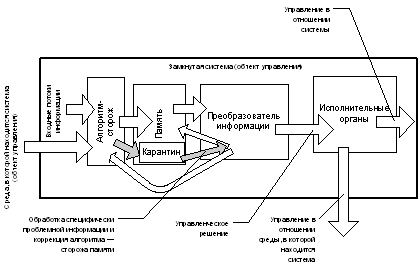
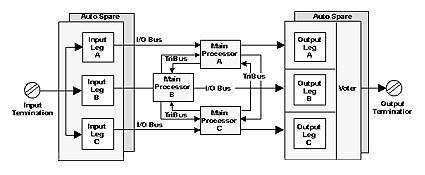
Ø Была дана общая характеристика случайной среды, системы управления, приведена её функциональная схема;
Ø На содержательном уровне дано определение конфликтности и потоков насыщения системы;
Ø Приведено математическое описание составляющих элементов системы и построен маркированный случайный точечный процесс, моделирующий динамическое поведение системы;
Ø Была доказана теорема марковости выделенной дискретной компоненты процесса ![]() .
.
Ø Выведены рекуррентные формулы для одномерных распределений дискретной компоненты маркированного точечного процесса ![]() .
.
Литература.
1. Куделин А.Н. Модель управления конфликтными потоками в случайной среде: “Теория вероятностей и математическая статистика. Диссертация на соискание уч. степени кандидата ф.-м.н”.
2. Бронштейн О.И. Рыков В.В., Об оптимальных дисциплинах обслуживания в управляемых системах // В сборн. "Управление производством", Тр. III Всесоюзн. совещ. по автоматическому управлению. Техническая кибернетика.- 1965.- М.: "Наука", 1967.
3. Рыков В.В. Управляемые системы массового обслуживания // Сборн. "Итоги науки. Теория вероятностей. Математическая статистика. Теоретическая кибернетика. ВИНИТИ АН СССР".
4. Файнберг М.А., Файнберг Е.А. Управление в системах массового обслуживания // "Зарубежная радиоэлектроника".
5. Федоткин М.А. Теория дискретных систем с переменной структурой обслуживания квазигенерирующих потоков : "Теория вероятностей и математическая статистика. Диссертация на соискание уч. степени доктора ф.-м.н.".
6. Федоткин М.А. Неполное описание потоков неоднородных требований. -"Теория массов. обслуж."
7. Чжун К.Л. Однородные цепи Маркова. –М.: Мир, 1964.
8. Феллер В. введение в теорию вероятностей и её приложения. Т.1, - М.: Мир, 1967.
9. Кантарович Л.В., Крылов В.И. Приблежённые методы высшего анализа. – М. –Л.: 'ГИФМЛ', 1962.
Похожие работы
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... БИОРЕАКТОРА Лист 90 Доклад. Уважаемые члены государственной экзаменационной комиссии разрешите представить вашему вниманию дипломный проект на тему: «Система автоматизированного управления процесса стерилизации биореактора» Процесс стерилизации биореактора (или ферментера) является важной стадией процесса биосинтеза антибиотика эритромицина. Суть процесса стерилизации состоит в ...
... высок и необходим курс мер по стабилизации социального напряжения в городе Нижнекамске. 3 Совершенствование организации системы профилактики социальной напряженности как фактора дестабилизации муниципальной среды управления 3.1 Долгосрочные социальные программы как универсальный метод стабилизации муниципальной среды управления Актуальность социальной проблематики в России сегодня ...
... формированию коллектива органа Г и М управления, социальные требования к условиям работы аппарата, перечень оргтехники и мебели. *Вопрос 7. Основные направления совершенствования современного государственного и муниципального управления. Государственное управление – это организующая исполнительно-распорядительная деятельность органов государственной власти, осуществляемая на основе и во ...
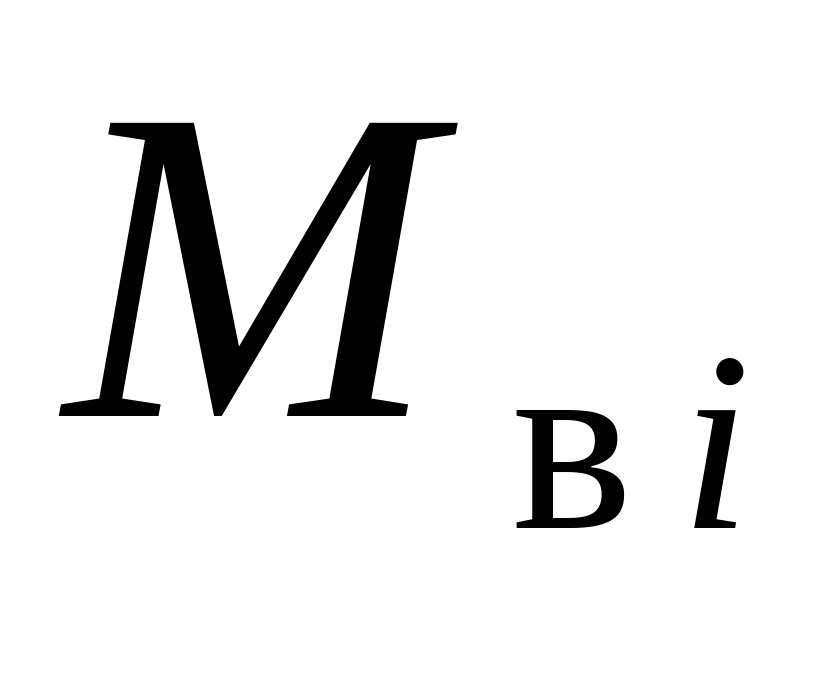
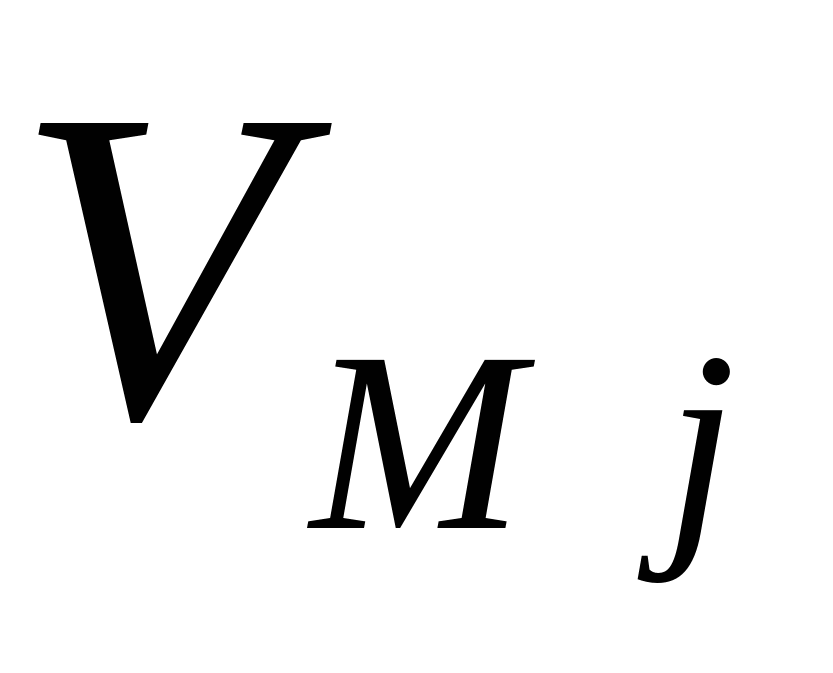
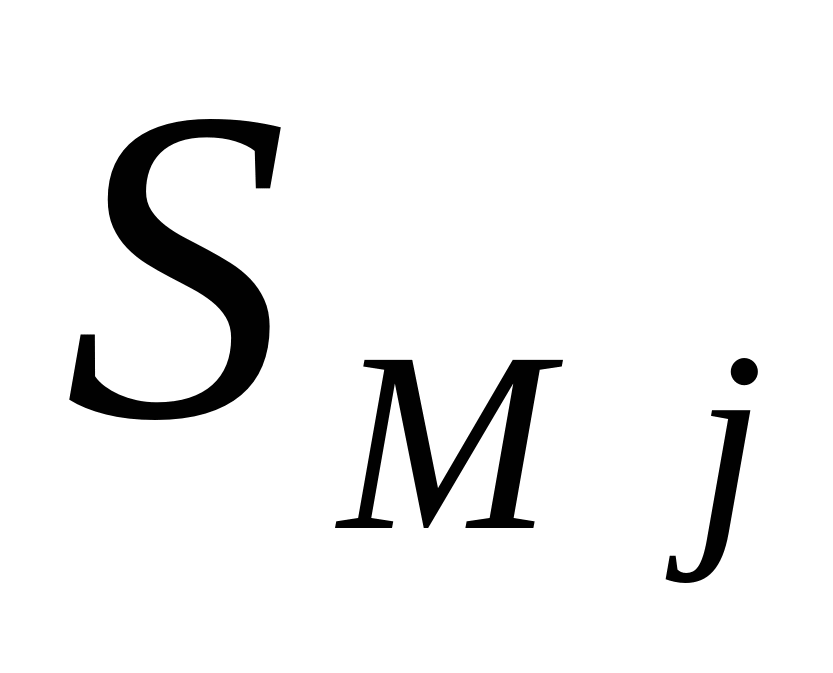
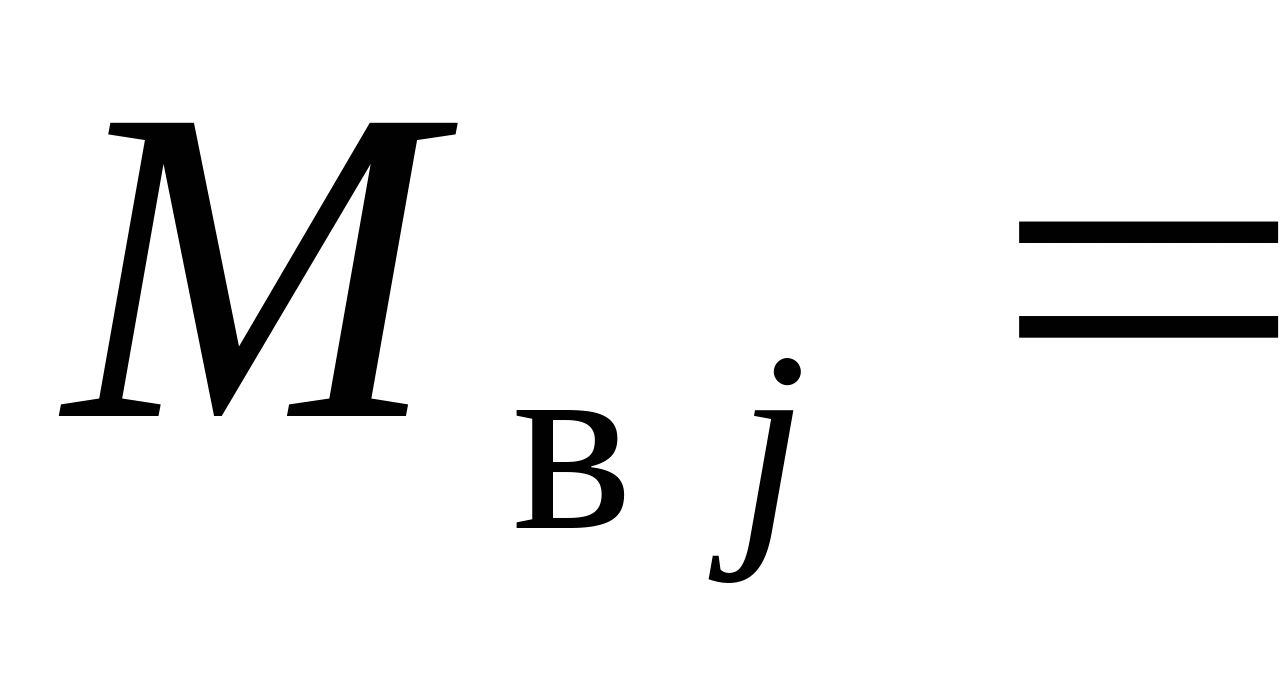
0 комментариев