Навигация
Методы относительных средних
37380
знаков
14
таблиц
0
изображений
4. Методы относительных средних.
Метод невзвешенных относительных средних.
В качестве альтернативы рассмотренным методам построения индексов, мы можем использовать метод невзвешенных относительных средних. При подсчете простого индекса (табл.1.1) уже была использована разновидность метода относительных средних. В том примере с одной измеряемой величиной мы подсчитали относительный процент путем деления количества корпораций в текущем году P1 на их количество в базовом году P2 затем умножили результат на 100.
Подсчет невзвешенного индекса относительных средних: В случае более чем одного наименования продукта или рода деятельности, сначала находится отношение текущей цены к базовой (для каждого продукта) и каждое отношение умножают на 100. Затем полученные значения складываются и результат делится на количество товаров.
(4.8)
Используя данные табл.3.4, рассчитаем индекс по методу невзвешенных относительных средних. Соответствующие вычисления приведены в табл.4.12 : индекс общего уровня цен для 1989 г. составляет 138. В табл.2.4 совокупный невзвешенный индекс был равен 145. Различие между двумя методами заключается в том, что в случае метода относительных средних мы рассчитываем среднее значение отношения цен по. всем продуктам, а в случае невзвешенного совокупного метода мы подсчитываем отношение сумм цен на все продукты. Заметим, что в рассматриваемом методе мы не присваиваем некоторым видам продуктов больший вес по сравнению с другими, а помещаем каждый элемент в относительную шкалу, где он представлен в виде процента, а не в виде денежной суммы. Таким образом каждый элемент группы оценивается относительно базы, принимаемой за 100%.
Таблица 4.12
Подсчет невзвешенного индекса относительных средних
| Продукт (1) | Цены 1984 г., долл. (2) | Цены 1989 г., долл. (3) | (3):(2)*100 (4) |
| Молоко (1 галлон) Яйца (1 дюжина) Гамбургер (1 фунт) Бензин (1 галлон) | 1.92 0.81 1.49 1.00 | 3.40 1.00 2.00 1.17 | 177 123 134 117 |
| S | 551 |
Невзв. индекс = 
= 
=138
Метод взвешенных относительных средних.
Во многих задачах требуется определять индексные числа, исходя из взвешивания в соответствии с важностью (значимостью) того или иного элемента, поэтому более распространенным является метод взвешенных относительных средних. В разделе 3, где подсчитывался взвешенный совокупный ценовой индекс, мы использовали объем потребления продукции в качестве весовых коэффициентов, тогда как в методе взвешенных относительных средних мы используем валовую стоимости каждого элемента группы (это величина получается умножением цены на количество).
Различные способы определения весов. В данном методе существует несколько способов определения взвешенных значений. Как и для индекса Ласпере, мы можем использовать базовую валовую стоимость, полученную умножением базового количества на базовую цену. Использование базовой стоимости приведет нас к тому же результату, что и в случае подсчета индекса по методу Ласпере. Поскольку результат одинаков, то решение об использовании метода Ласпере или метода взвешенных относительных средних часто зависит от возможности получения самих данных. Если более доступными являются данные о стоимости товаров, то используется метод взвешенных относительных средних. Мы применяем индекс Ласпере, если проще и дешевле получить количественные данные.
Подсчет взвешенного индекса относительного среднего:
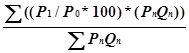(4.9)
PnQn- стоимость;
P1- цены текущего периода;
P0- цены базового периода.
Pn и Qn - цены и количества, которые определяют значения, используемые нами как веса. В частности:
n = 0 для базового периода:
n = 1 для текущего периода;
n = 2 для фиксированного периода.
Следовательно, в случае базовых стоимостей формула (3.7) примет вид:
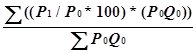(4.10)
Соотношение между данными методом и методом Ласпере: расчет по формуле (4.10) эквивалентен расчету индекса Ласпере для любой задачи.
В особых случаях в общей формуле возможно использование стоимостей, полученных умножением цены из одного периода на количество из другого периода.
Пример: Данные, приведенные в табл.4.13 были взяты из табл.3.9. Поскольку мы имеем цены и количества базового периода, то расчеты будем делать по формуле (4.10). Ценовой индекс, равный 122, немного отличается от 121, полученного в табл.3.7. Расхождение объясняется промежуточными округлениями.
Таблица 4.13
Подсчет взвешенного индекса относительных средних
| Элементы | P0 | P1 | Q0 | P1:P0 | P0Q2 | Взвеш. относит |
| Совокупного | Средняя цена (долл.) | Среднее колич. | (3):(2)*100 | Базовая стоимость | процент | |
| Индекса (1) | 1985 г. (2) | 1989 г. (3) | продуктов потреб. семьей в 1984 г. (4) |
(5) | (2)*(4) (6) | (5)*(6) (7) |
| Хлеб, бух. Картофель,фунт Курица, шт. | 0.91 0.79 3.92 | 1.19 0.99 4.50 | 200 300 100 | 131 125 115 | 182 237 392 | 23842 29625 45080 |
| S | 811 | 98547 | ||||
Индекс = 
= 122
Использование базовых, фиксированных и текущих стоимостей
В случаях базовых стоимостей P0Q0 или фиксированных стоимостей P1Q1 мы можем сравнивать уровни цен разных периодов. Однако при использовании текущих стоимостей P1Q1 мы не можем непосредственно сравнивать значения разных периодов, так как и цены, и количества могли изменится. Поэтому при вычислении индекса взвешенных относительных средних обычно используются либо базовые, либо фиксированные стоимости.
Похожие работы
... степень влияния каждого из факторов на общую динамику средней. Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных ...
... применение данных методов значительно улучшает анализ внешней торговли, вскрывает неиспользованные резервы, тем самым способствуя в целом повышению эффективности ВЭС. 3.МЕТОДОЛОГИЯ ПРИМЕНЕНИЯ ИНДЕКСНОГО МЕТОДА В ТАМОЖЕННОЙ СТАТИСТИКЕ В качестве первичной исходной информации при формировании индексов внешней торговли РФ используются данные, содержащиеся в грузовых таможенных декларациях (ГТД ...
... . · Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя. · Работа с факторной моделью (практическое ее использование для управления экономическими процессами). 2. Измерение влияния факторов в индексном анализе Индекс - это статистический показатель, представляющий собой отношение двух состояний какого-либо признака. С помощью ...
... квартиры отличаются в среднем от средней арифметической цены на 1,8 тысяч рублей. % Значение коэффициента вариации (8,9 %) свидетельствует о том, что совокупность цен на трехкомнатные квартиры однородна. 2.5 Применение индексного метода анализа цен По формуле (19) рассчитаем цепные и базисные индексы цен Ласпейреса. Цепные индексы цен Ласпейреса: Зная, что произведение ...
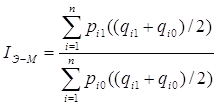
0 комментариев