Навигация
Теорема Дирихле
2.3. Теорема Дирихле.
Выше
мы нашли оценку
погрешности,
возникающей
при замене
любого действительного
числа ![]() рациональными
дробями определенного
типа, а именно:
подходящими
дробями.
рациональными
дробями определенного
типа, а именно:
подходящими
дробями.
А сейчас рассмотрим некоторые сравнительно простые результаты, показывающие как обстоит дело с приближением действительных чисел рациональными числами, не предрешая заранее, что эти рациональные числа будут подходящими дробями.
Пусть ![]() –
произвольное
действительное
число. Из теории
десятичных
дробей следует
существование
рационального
числа
–
произвольное
действительное
число. Из теории
десятичных
дробей следует
существование
рационального
числа
![]() такого, что
такого, что ![]() .
поставим вопрос
о возможности
таких приближений
.
поставим вопрос
о возможности
таких приближений
![]() рациональными
числами
рациональными
числами ![]() ,
при которых
точность приближения
будет оценена
не величиной
,
при которых
точность приближения
будет оценена
не величиной ![]() ,
а величиной,
в
,
а величиной,
в
![]() раз
меньшей, то
есть вопрос
о нахождении
рациональных
чисел
раз
меньшей, то
есть вопрос
о нахождении
рациональных
чисел
![]() таких, что
таких, что ![]() ,
где
,
где ![]() – любое
заранее положительное
число.
– любое
заранее положительное
число.
Например,
можно поставить
задачу нахождения
такого рационального
приближения
к ![]() ,
чтобы точность
приближения
была в
1000 или
в
1000000 раз
лучшей, чем
величина, обратная
знаменателю.
Это соответствует
выбору
,
чтобы точность
приближения
была в
1000 или
в
1000000 раз
лучшей, чем
величина, обратная
знаменателю.
Это соответствует
выбору
![]() =1000
или
=1000
или ![]() =1000000.
оказывается,
что как бы велико
ни было
=1000000.
оказывается,
что как бы велико
ни было ![]() ,
можно найти
рациональную
дробь
,
можно найти
рациональную
дробь ![]() ,
приближающую
,
приближающую
![]() с точностью
до
с точностью
до ![]() ,
причем и это
является самым
интересным,
дробь
,
причем и это
является самым
интересным,
дробь
![]() мы можем выбрать
так, что
мы можем выбрать
так, что ![]() .
.
Теорема
Дирихле:
Пусть
![]() и
и ![]() –
действительные
числа; существует
несократимая
дробь
–
действительные
числа; существует
несократимая
дробь ![]() ,
для которой
,
для которой
![]() ,
,
![]()
(или:
существует
такая пара
взаимно простых
целых чисел
a
и b,
что ![]() ,
, ![]() ).
).
Доказательство: Теорему легко доказать с помощью аппарата цепных дробей.
Пусть
![]() подходящая
дробь числа
подходящая
дробь числа ![]() ;
выберем наибольший
из знаменателей
;
выберем наибольший
из знаменателей
![]() ,
не превышающий
,
не превышающий ![]() ,
то есть наибольшее
k,
чтобы
,
то есть наибольшее
k,
чтобы ![]()
![]() и положим
и положим ![]() =
=![]() .
Рассмотрим
два случая:
.
Рассмотрим
два случая:
![]() не является последним знаменателем, то есть существует
не является последним знаменателем, то есть существует ![]() такое, что
такое, что ![]()
![]()
![]() . Тогда при a=
. Тогда при a=![]() и b=
и b=![]() имеем:
имеем:
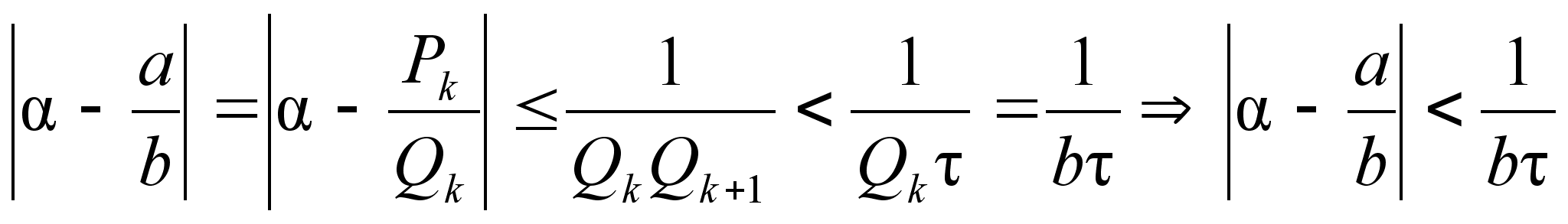
2) ![]() –
знаменатель
последней
подходящей
дроби разложения
–
знаменатель
последней
подходящей
дроби разложения ![]() ,
то есть
,
то есть ![]() =
=![]() .
Тогда при a=
.
Тогда при a=![]() ,
b=
,
b=![]() ,
имеем:
,
имеем:
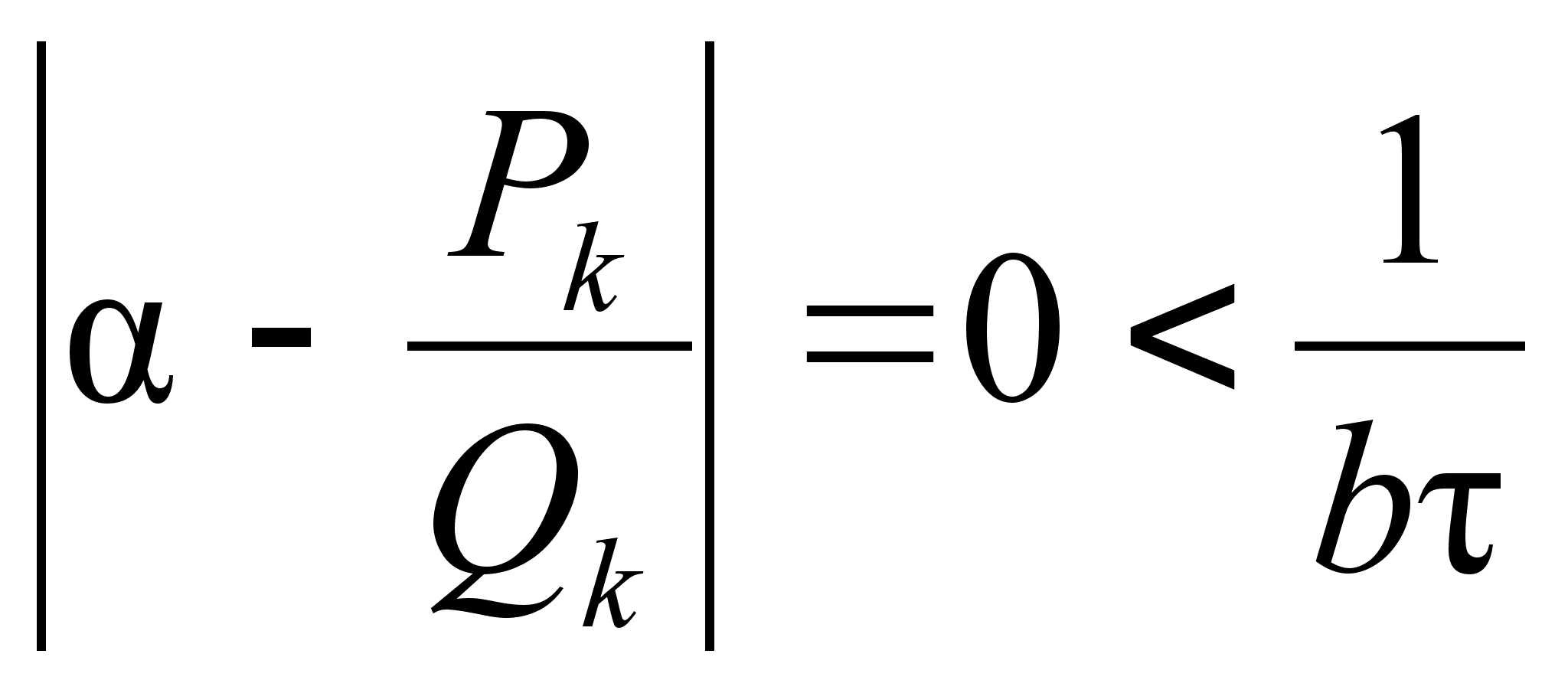 .
.
Теорема доказана.
Сам Дирихле дал другое доказательство, использовав в нем принцип, который носит теперь имя Дирихле: при распределении N объектов между N-1 ящиками хотя бы в одном ящике должно находиться 2 объекта. Приведем это доказательство.
Пусть
![]() ,
рассмотрим
совокупность
t+2
чисел, состоящую
из
1 и
значений дробных
частей
,
рассмотрим
совокупность
t+2
чисел, состоящую
из
1 и
значений дробных
частей
![]() для x=0,
1, …, t
(причем
для x=0,
1, …, t
(причем ![]() =
=![]() -
-![]() ,
, ![]() ).
Очевидно, каждое
из чисел этой
совокупности
принадлежит
точно одному
из
t+1
промежутков
).
Очевидно, каждое
из чисел этой
совокупности
принадлежит
точно одному
из
t+1
промежутков
![]() ,
,
![]() ,
…,
,
…, ![]() ,
из которых
первые
t
являются
полусегментами,
а последний
сегментом.
,
из которых
первые
t
являются
полусегментами,
а последний
сегментом.
————![]() ————
————![]() ————
————![]() ——————————————
——————————————![]() ————
————![]() ——
——
0 ![]()
![]()
![]() 1
1
Так
как чисел у нас
t+2,
то (согласно
принципу Дирихле)
обязательно
найдется такой
промежуток,
который содержит
2 числа
из совокупности
![]() и 1.
Разность этих
двух чисел не
превосходит
длину содержащего
их промежутка,
то есть
и 1.
Разность этих
двух чисел не
превосходит
длину содержащего
их промежутка,
то есть ![]() .
.
Если такими числами являются ![]() и
и ![]() , то
, то ![]() . Пусть
. Пусть ![]() и
и ![]() ,
, ![]() . Так как
. Так как ![]() , то
, то ![]() ,
, ![]() ).
).
Если ![]() и 1 принадлежат одному промежутку, то
и 1 принадлежат одному промежутку, то
![]()
Пусть
в таком случае
![]() ,
,
![]() .
Очевидно, и
здесь
.
Очевидно, и
здесь ![]() ,
так что
,
так что ![]() ,
, ![]() ).
).
Теорема доказана.
Рассмотрим пример применения теоремы Дирихле.
Найти
рациональное
приближение
![]() к
к
![]() с точностью
до
с точностью
до ![]() .
.
Решение:
Разложим
![]() в цепную дробь.
в цепную дробь.
![]() =2
=2
![]() -21,
то
-21,
то ![]() ,
то есть если
,
то есть если
![]()
![]() ,
то
,
то ![]() .
.
Доказательство:
Рассмотрим
случай, когда
![]() (иначе теряет
смысл). Тогда
(иначе теряет
смысл). Тогда ![]() всегда лежит
между любыми
двумя последующими
подходящими
дробями так,
что для
k>1
всегда лежит
между любыми
двумя последующими
подходящими
дробями так,
что для
k>1 ![]() всегда лежит
между
всегда лежит
между
![]() и
и ![]() ,
причем ближе
к
,
причем ближе
к ![]() ,
чем к
,
чем к ![]() .
Поэтому, если
.
Поэтому, если
![]() ближе к
ближе к ![]() ,
чем
,
чем ![]() ,
то оно находится
между
,
то оно находится
между
![]() и
и ![]() .
В случае четного
.
В случае четного
![]() можно записать
можно записать
![]()
![]()
![]() (в случае нечетного
k
доказательство
существенно
не меняется),
откуда
(в случае нечетного
k
доказательство
существенно
не меняется),
откуда ![]() ,
или
,
или ![]() ,
,![]()
![]()
![]() ,
откуда, домножая
неравенство
на
,
откуда, домножая
неравенство
на ![]() ,
получаем
,
получаем ![]() .
Так как
.
Так как ![]() – число целое
и положительное,
то из предыдущего
равенства
следует
– число целое
и положительное,
то из предыдущего
равенства
следует ![]() ,
что и требовалось
доказать.
,
что и требовалось
доказать.
Попутно
мы установили,
что любая
рациональная
дробь ![]() ,
принадлежащая
интервалу
,
принадлежащая
интервалу ![]() ,
k>1,
имеет знаменатель
,
k>1,
имеет знаменатель
![]() .
Для
k=1
теорема неверна:
.
Для
k=1
теорема неверна:
![]() может
оказаться ближе
к
может
оказаться ближе
к ![]() ,
чем его подходящая
дробь
,
чем его подходящая
дробь ![]() ,
хотя
,
хотя ![]() .
.
Доказанная теорема приводит нас к следующему определению:
Рациональную
дробь
![]() называют наилучшим
приближением
действительного
называют наилучшим
приближением
действительного ![]() ,
если любая
более близкая
к
,
если любая
более близкая
к ![]() рациональная
дробь
рациональная
дробь
![]() имеет больший
знаменатель,
чем
имеет больший
знаменатель,
чем ![]() ,
то есть если
из
,
то есть если
из
![]() следует d>b.
следует d>b.
Таким
образом, подходящие
дроби являются
наилучшими
приближениями,
например, Архимедово
число ![]() для
для
![]() является наилучшим
приближением.
является наилучшим
приближением.
Ранее
мы доказали,
что для оценки
погрешности ![]() ,
возникающей
при замене
любого действительного
,
возникающей
при замене
любого действительного ![]() его подходящей
дробью
его подходящей
дробью ![]() ,
можно пользоваться
неравенством
,
можно пользоваться
неравенством ![]() .
Выразим этот
результат по
отношению к
действительному
иррациональному
.
Выразим этот
результат по
отношению к
действительному
иррациональному
![]() ,
имеющим бесконечное
множество
подходящих
дробей, следующим
образом: для
любого действительного
иррационального
,
имеющим бесконечное
множество
подходящих
дробей, следующим
образом: для
любого действительного
иррационального ![]() существует
при
c=1
бесконечное
множество
несократимых
дробей
существует
при
c=1
бесконечное
множество
несократимых
дробей
![]() таких, что
таких, что 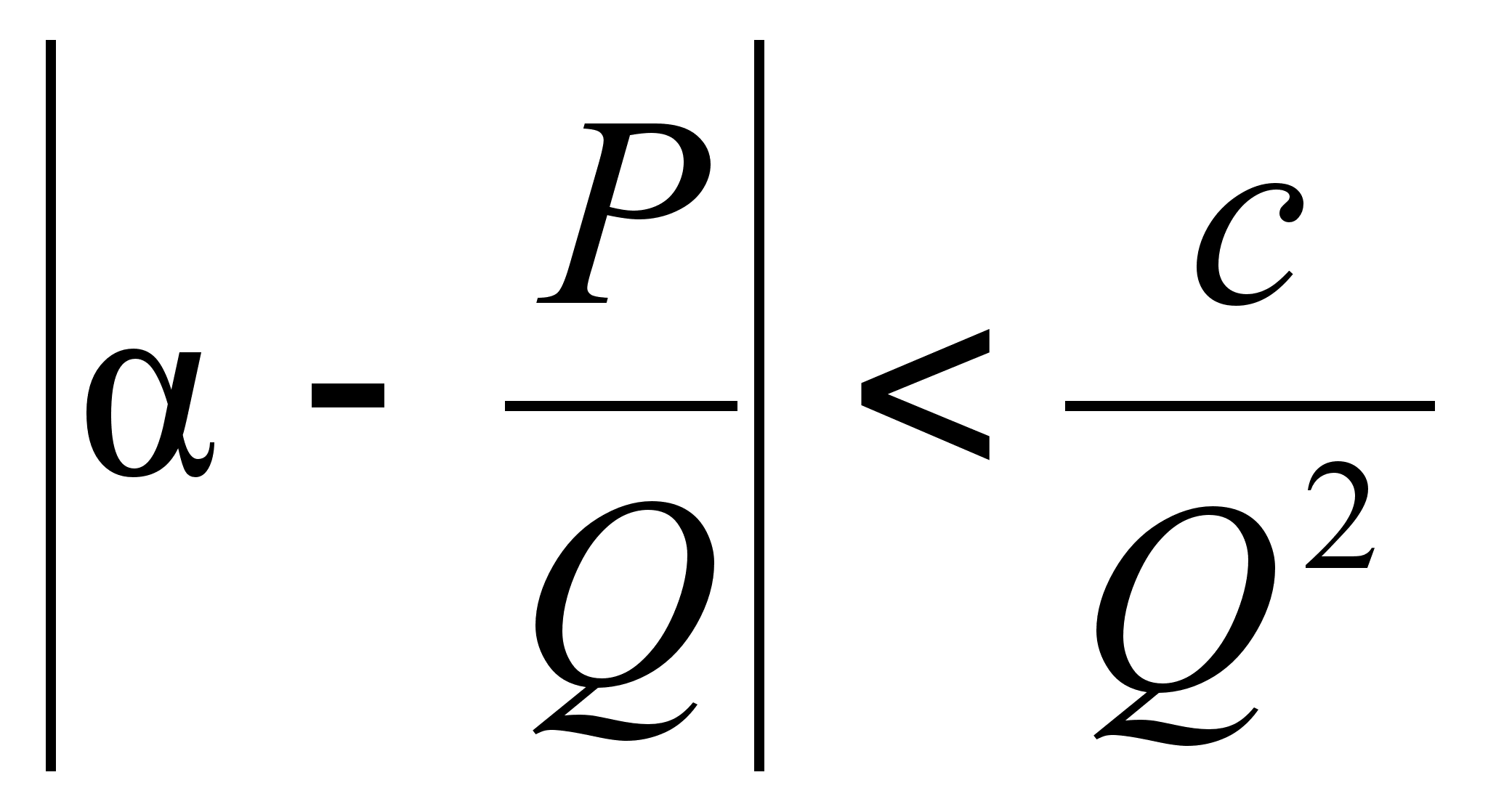 (1).
(1).
Такими
дробями являются,
например, все
подходящие
дроби для ![]()
![]() .
.
Возникает
вопрос: При
каких меньших
значениях
c
(чем c=1)
существует
для любого
действительного
иррационального ![]() бесконечное
множество
(несократимых)
рациональных
приближений
бесконечное
множество
(несократимых)
рациональных
приближений ![]() ,
погрешность
которых
,
погрешность
которых ![]() .
.
Теорема:
Для любого
действительного
иррационального
числа ![]() существует
при
существует
при
![]() бесконечное
множество
несократимых
рациональных
дробей
бесконечное
множество
несократимых
рациональных
дробей
![]() таких, что
таких, что 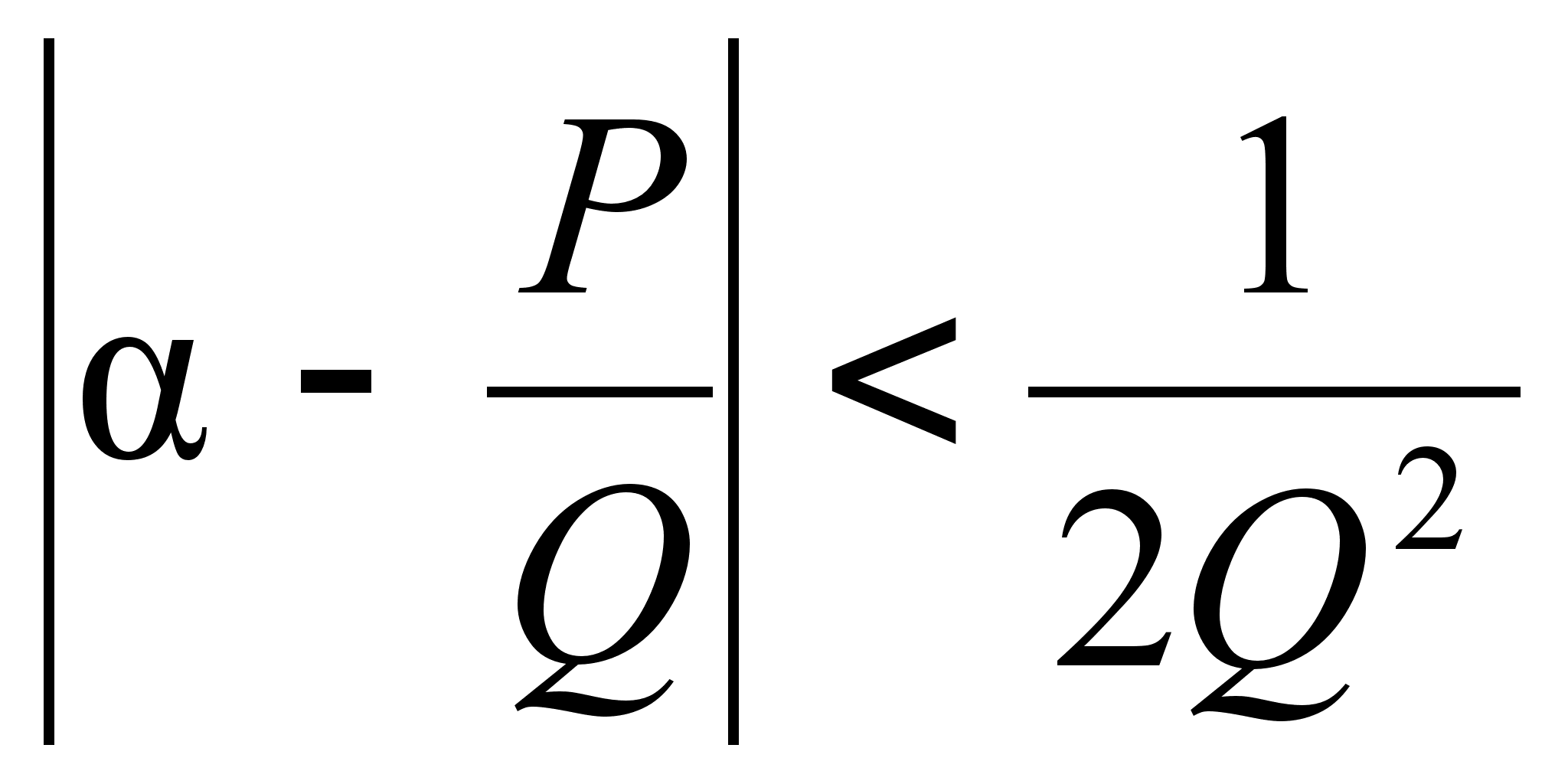 (
(![]() ).
Такими рациональными
дробями могут
быть только
подходящие
дроби к
).
Такими рациональными
дробями могут
быть только
подходящие
дроби к ![]() .
.
Доказательство:
Докажем первую
часть теоремы.
Рассмотрим
две последующие
подходящие
дроби к ![]()
![]() и
и ![]() .
Допустим, что
ни одна из этих
дробей не
удовлетворяет
неравенству
(
.
Допустим, что
ни одна из этих
дробей не
удовлетворяет
неравенству
(![]() ).
Тогда имеем:
).
Тогда имеем:
![]() ,
,
![]() .
Отсюда
.
Отсюда 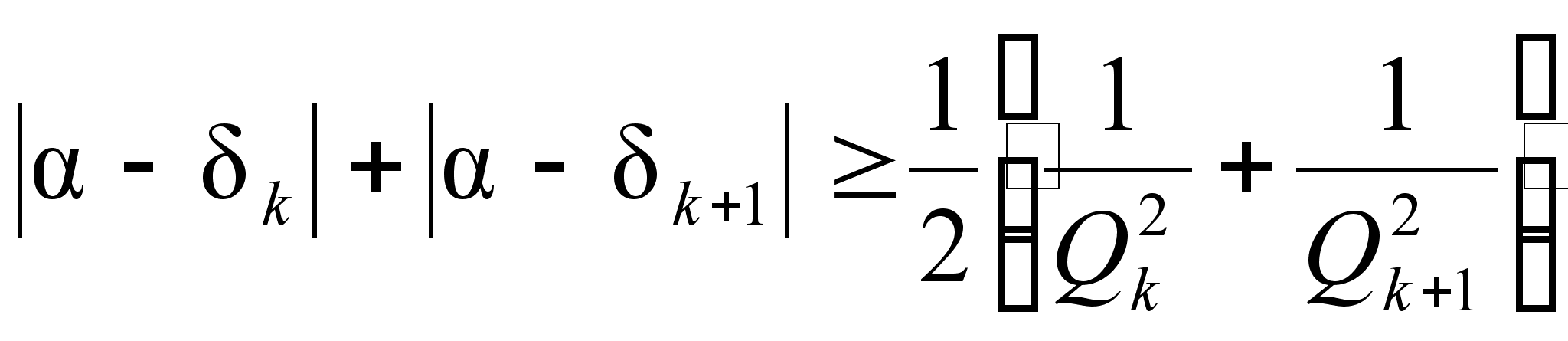 .
.
Но
так как ![]() лежит между
лежит между
![]() и
и ![]() ,
то
,
то ![]()
![]() ,
вследствие
чего
,
вследствие
чего 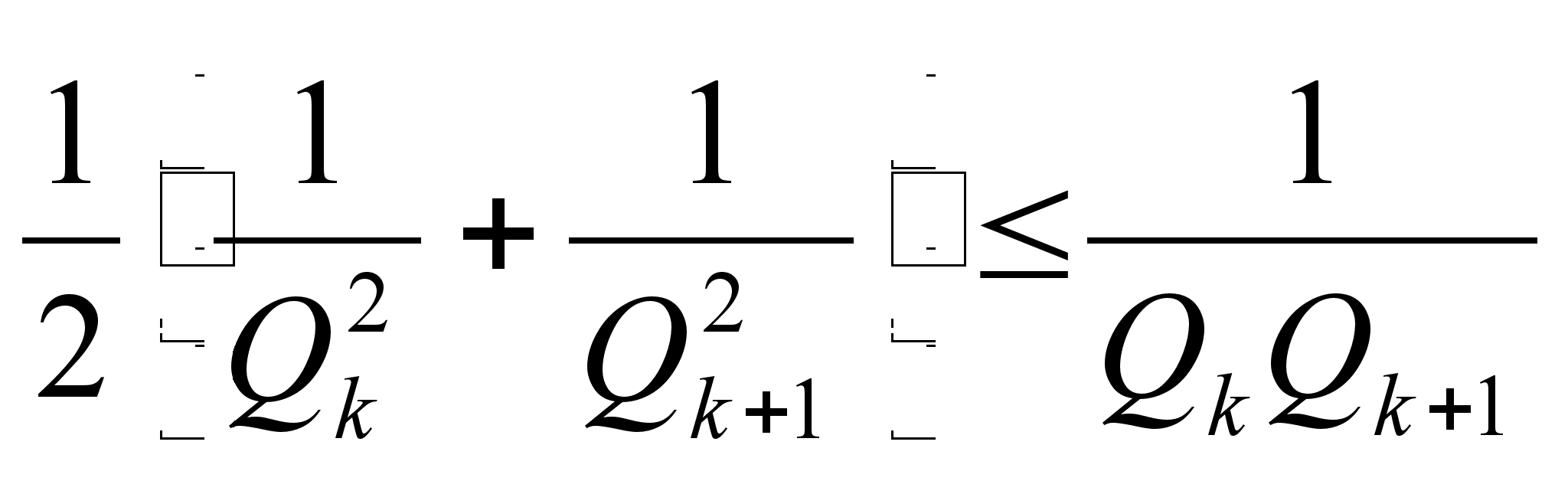 ,
или
,
или 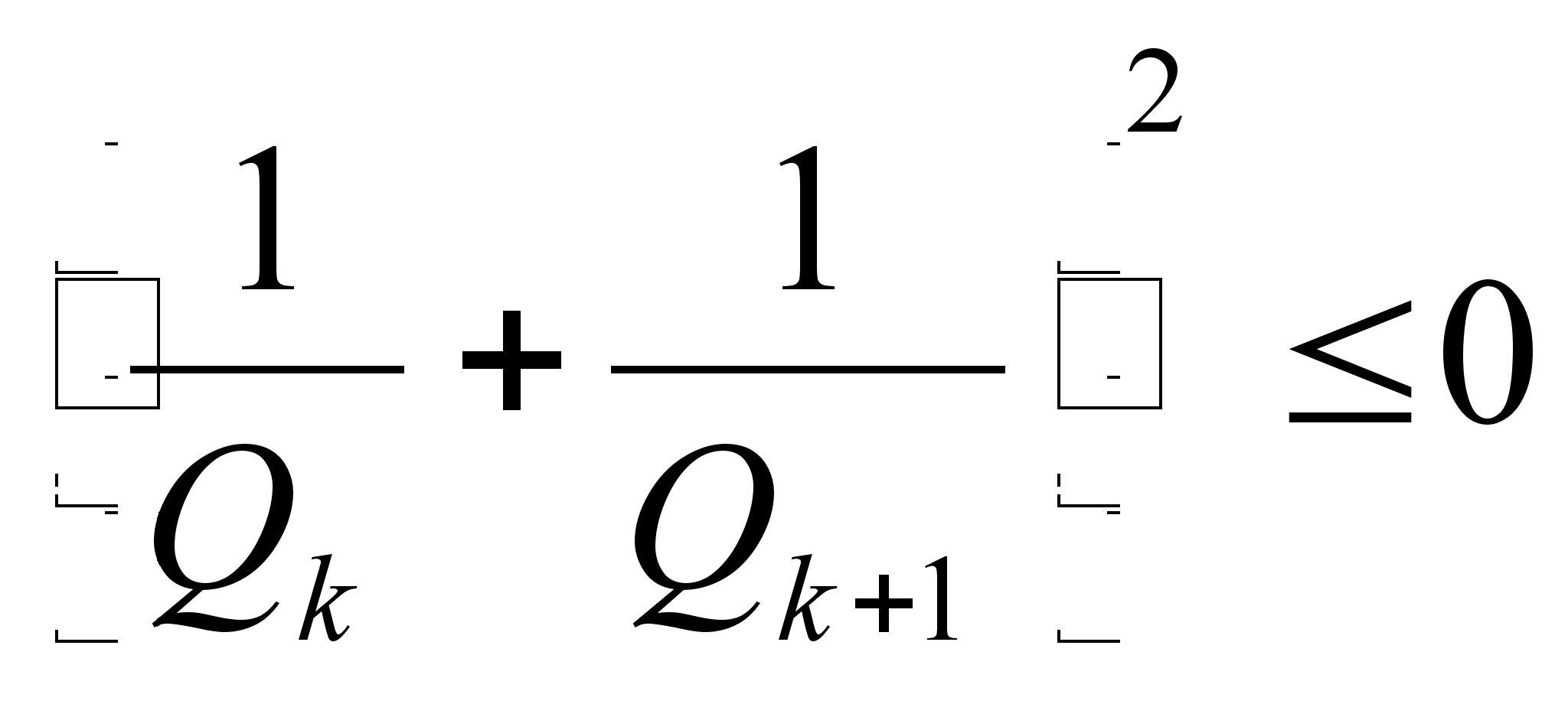 ,
а это для
k>1
невозможно.
Мы пришли к
противоречию,
значит наше
допущение
неверно, а верно
то, что требуется
доказать.
,
а это для
k>1
невозможно.
Мы пришли к
противоречию,
значит наше
допущение
неверно, а верно
то, что требуется
доказать.
Для
доказательства
второй части
теоремы докажем
достаточный
признак подходящей
дроби к действительному
числу ![]() :
если
:
если ![]() ,
где Q>0,
несократимая
дробь и для
действительного
,
где Q>0,
несократимая
дробь и для
действительного ![]() имеет место
неравенство
(
имеет место
неравенство
(![]() ),
то
),
то
![]() является подходящей
дробью к
является подходящей
дробью к ![]() .
.
Доказательство:
Покажем, что
если
![]() =(
=(![]() )=
)=![]() (
(![]() удовлетворяет
условию теоремы)
подходящая
дробь к
удовлетворяет
условию теоремы)
подходящая
дробь к ![]() ,
то соответствующее
остаточное
число
,
то соответствующее
остаточное
число ![]() разложения
данного
разложения
данного ![]() в цепную дробь
окажется >1.
Действительно,
в цепную дробь
окажется >1.
Действительно,
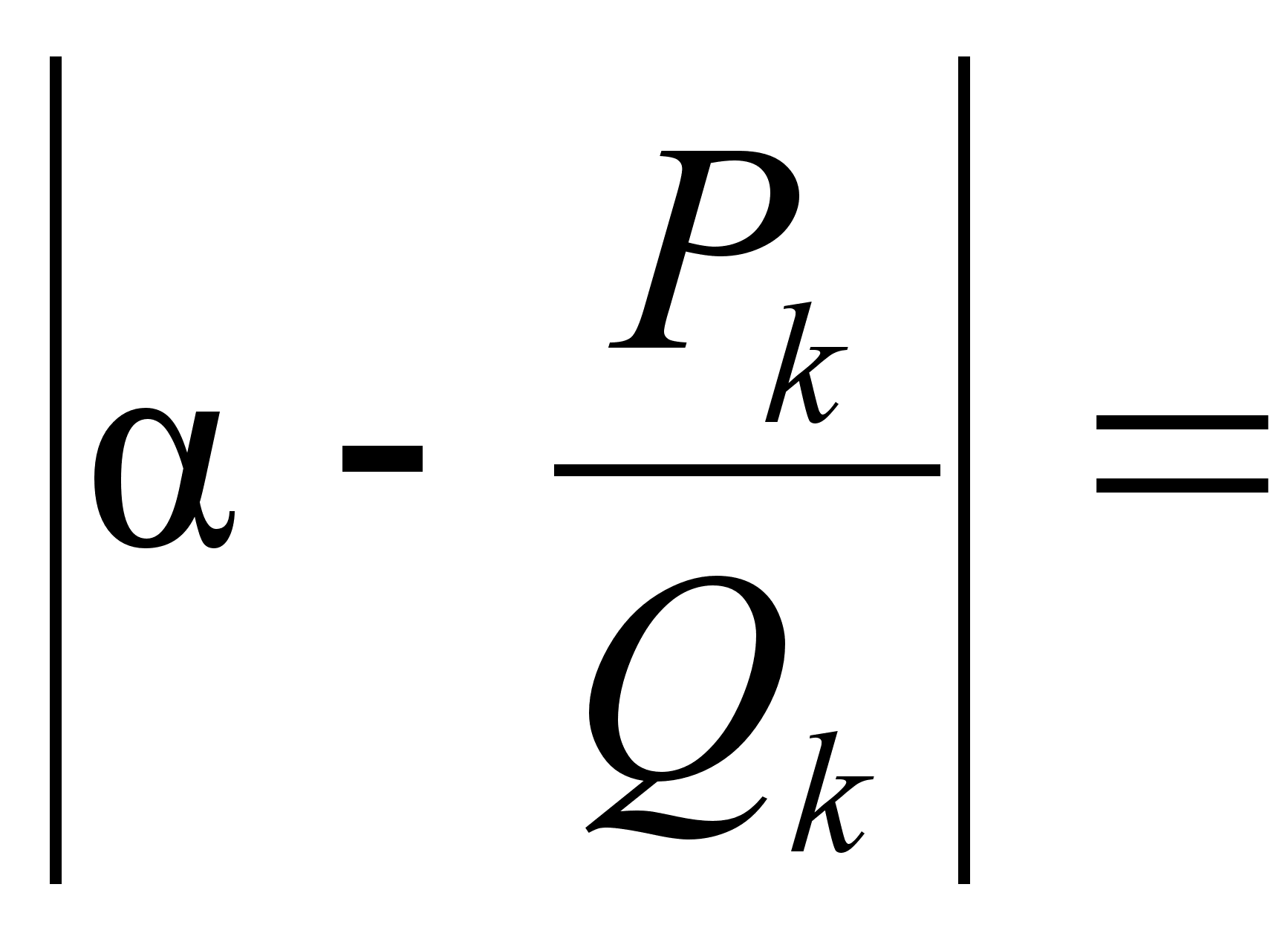
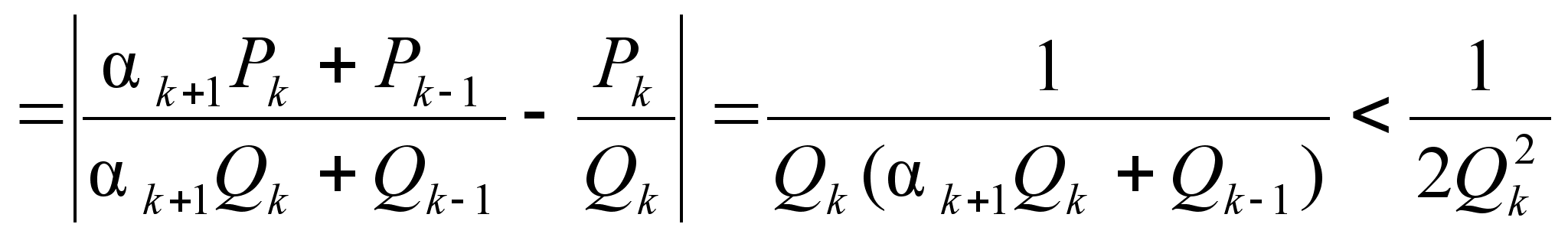 ,
откуда следует
,
откуда следует
![]() ,
так как
,
так как ![]() .
.
Теорема доказана полностью.
Достаточный
признак подходящей
дроби не является
ее необходимым
признаком;
могут существовать
подходящие
дроби для ![]() ,
которые ему
не удовлетворяют.
,
которые ему
не удовлетворяют.
Крайнюю возможность уменьшения c в указанном раньше смысле выражает теорема Гурвица-Бореля:
Теорема:
Для любого
действительного
иррационального
числа ![]() существует
при
существует
при
![]() бесконечное
множество
несократимых
рациональных
дробей
бесконечное
множество
несократимых
рациональных
дробей
![]() таких, что
выполняется
неравенство
(1),
то есть неравенство
таких, что
выполняется
неравенство
(1),
то есть неравенство
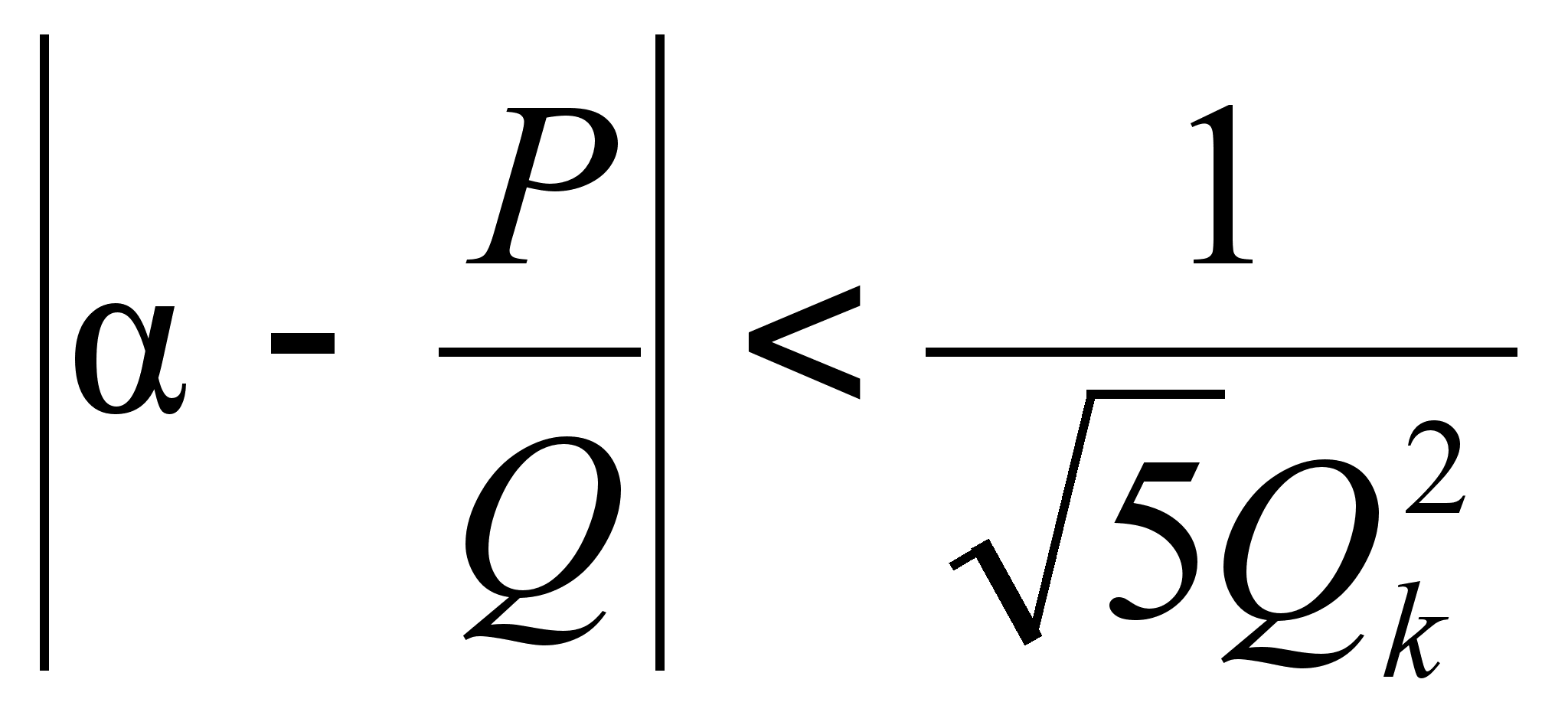 ,
(
,
(![]() )
)
если
же ![]() ,
то существуют
такие действительные
иррациональные
,
то существуют
такие действительные
иррациональные
![]() ,
для которых
неравенство
(1) имеет
не более конечного
числа рациональных
решений
,
для которых
неравенство
(1) имеет
не более конечного
числа рациональных
решений ![]() .
.
Доказательство:
Докажем первую
часть. Разложим ![]() в цепную дробь.
Мы докажем, что
из трех любых
соседних подходящих
дробей
в цепную дробь.
Мы докажем, что
из трех любых
соседних подходящих
дробей ![]() ,
i=k,
k+1,
k+2
по
крайней мере
одна удовлетворяет
условию
,
i=k,
k+1,
k+2
по
крайней мере
одна удовлетворяет
условию ![]() .
Доказательство
этого утверждения
будем вести
методом от
противного.
Предположим,
что для каких-либо
трех соседних
подходящих
дробей выполняются
неравенства:
.
Доказательство
этого утверждения
будем вести
методом от
противного.
Предположим,
что для каких-либо
трех соседних
подходящих
дробей выполняются
неравенства:
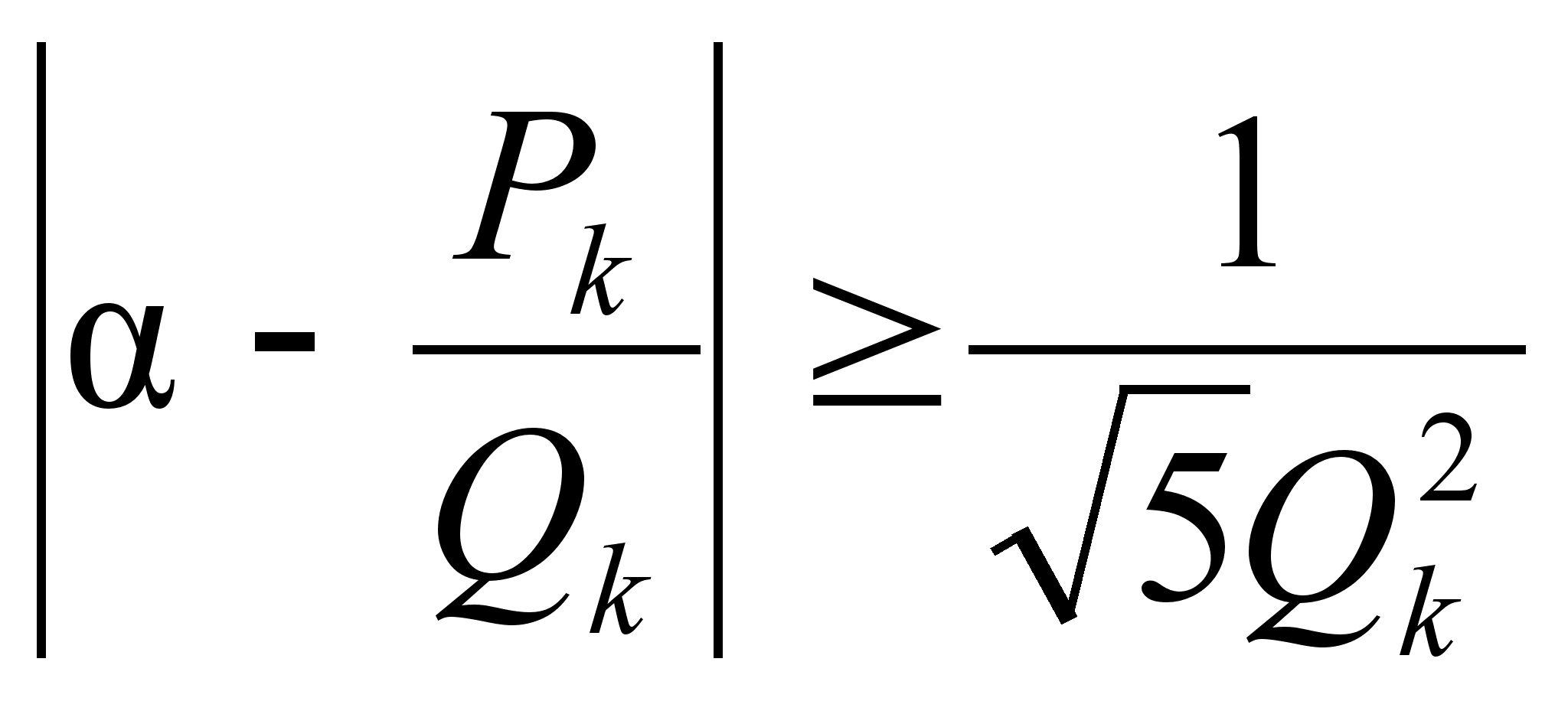 ,
, 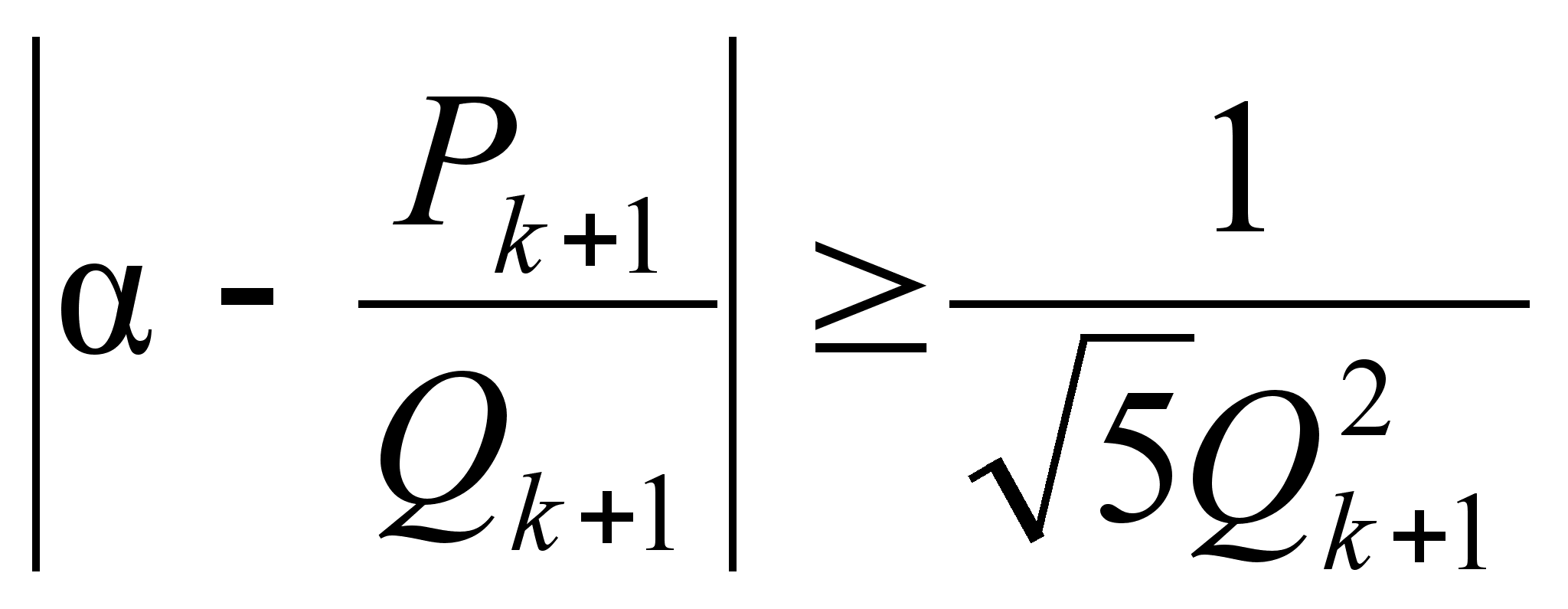 ,
,
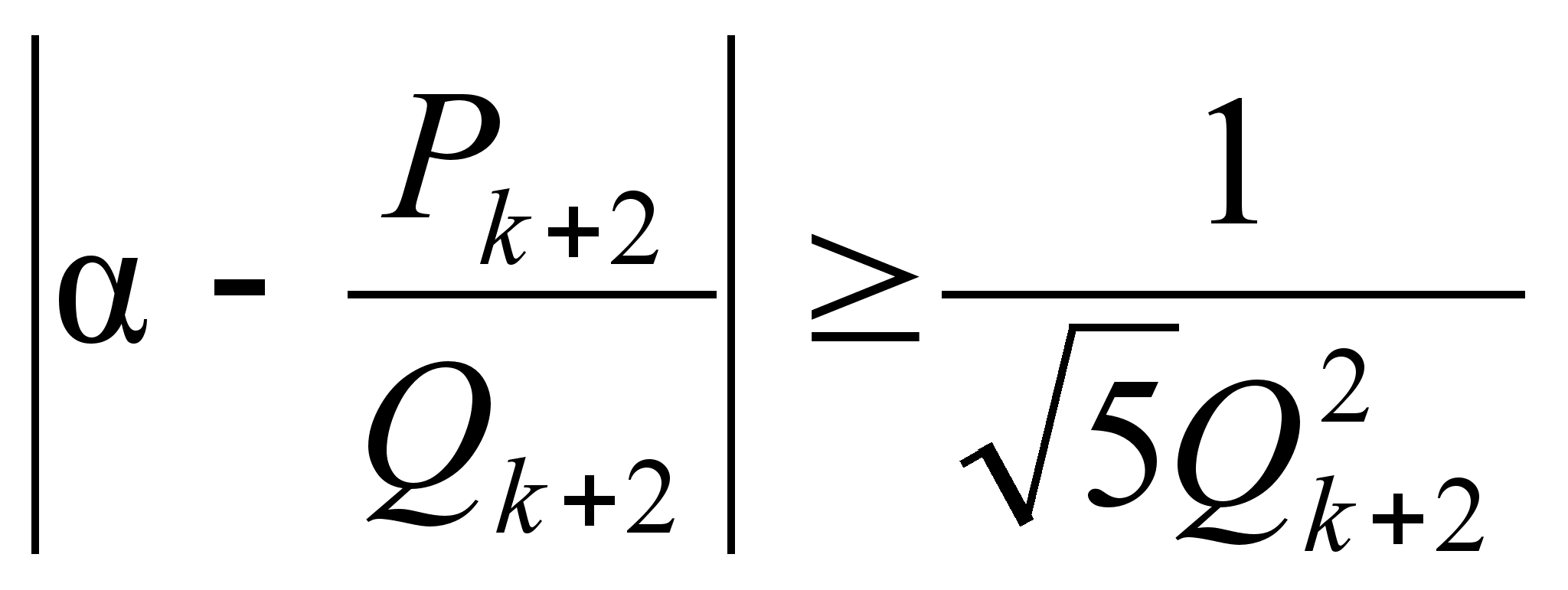 (2)
(2)
![]() и
и ![]() расположены
по разные стороны
от
расположены
по разные стороны
от ![]() и поэтому при
нечетном
k
из
(2) следует
и поэтому при
нечетном
k
из
(2) следует
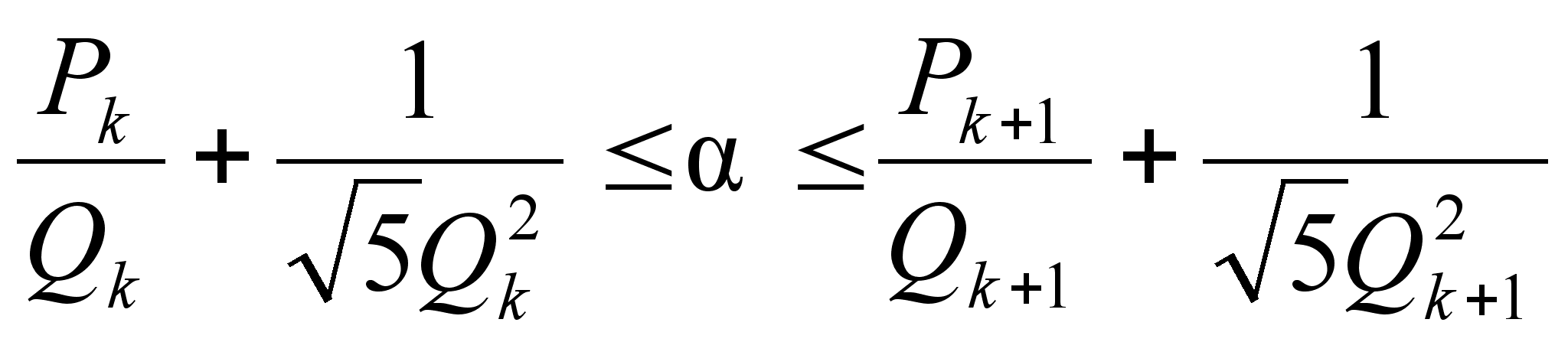 ,
,
а
при четном: 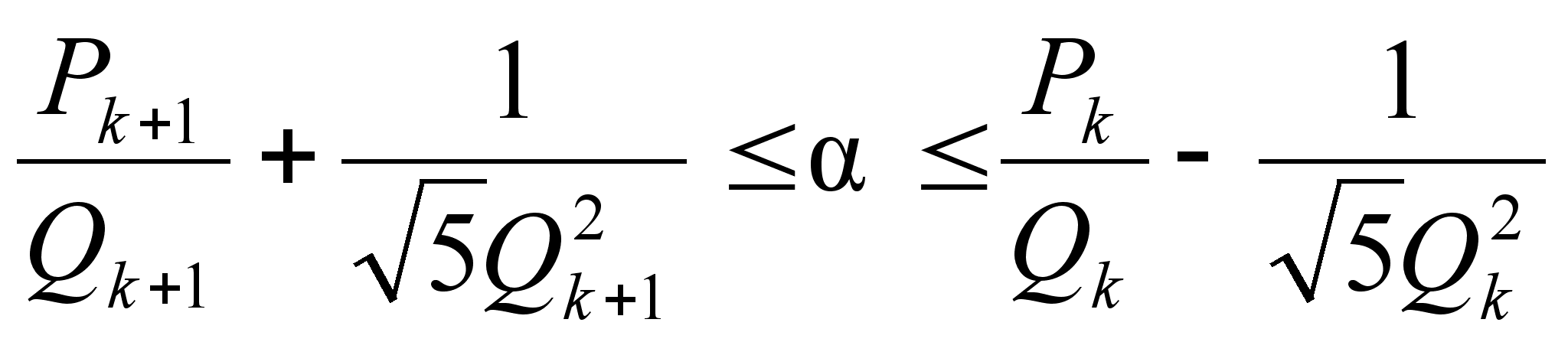 ,
так что и в том,
и в другом случае
имеем:
,
так что и в том,
и в другом случае
имеем:
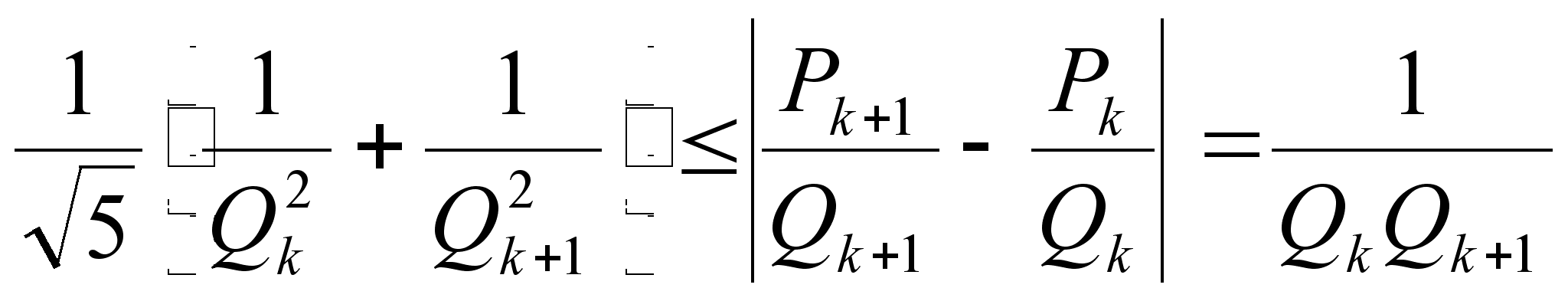
,
или, умножая
на
![]() и перенося все
члены в одну
сторону
и перенося все
члены в одну
сторону 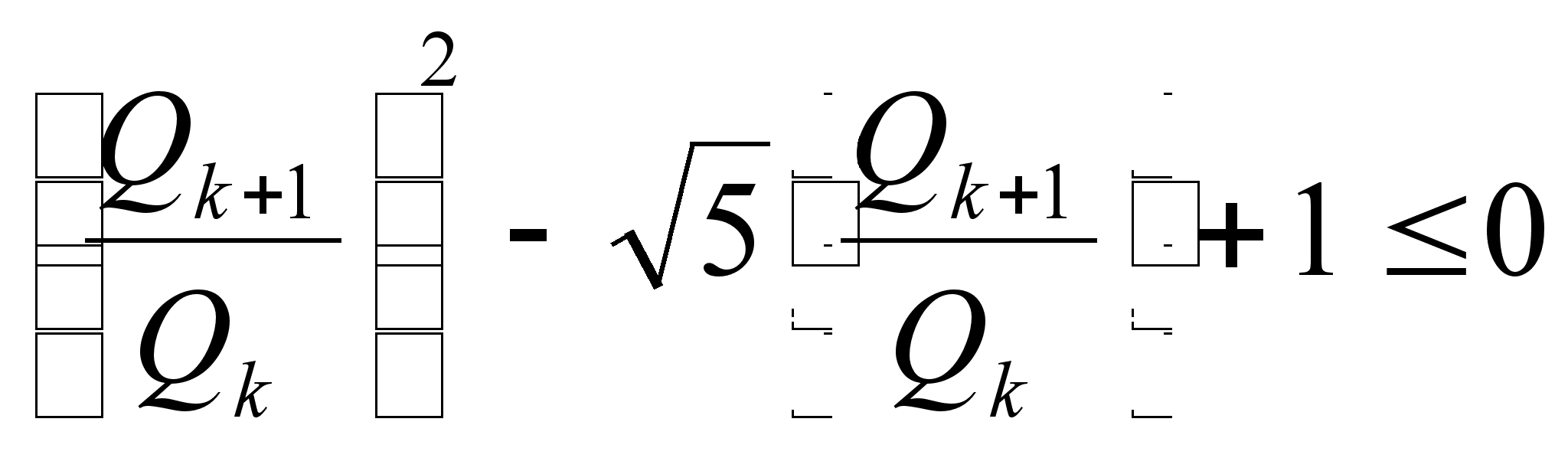 ,
то есть
,
то есть 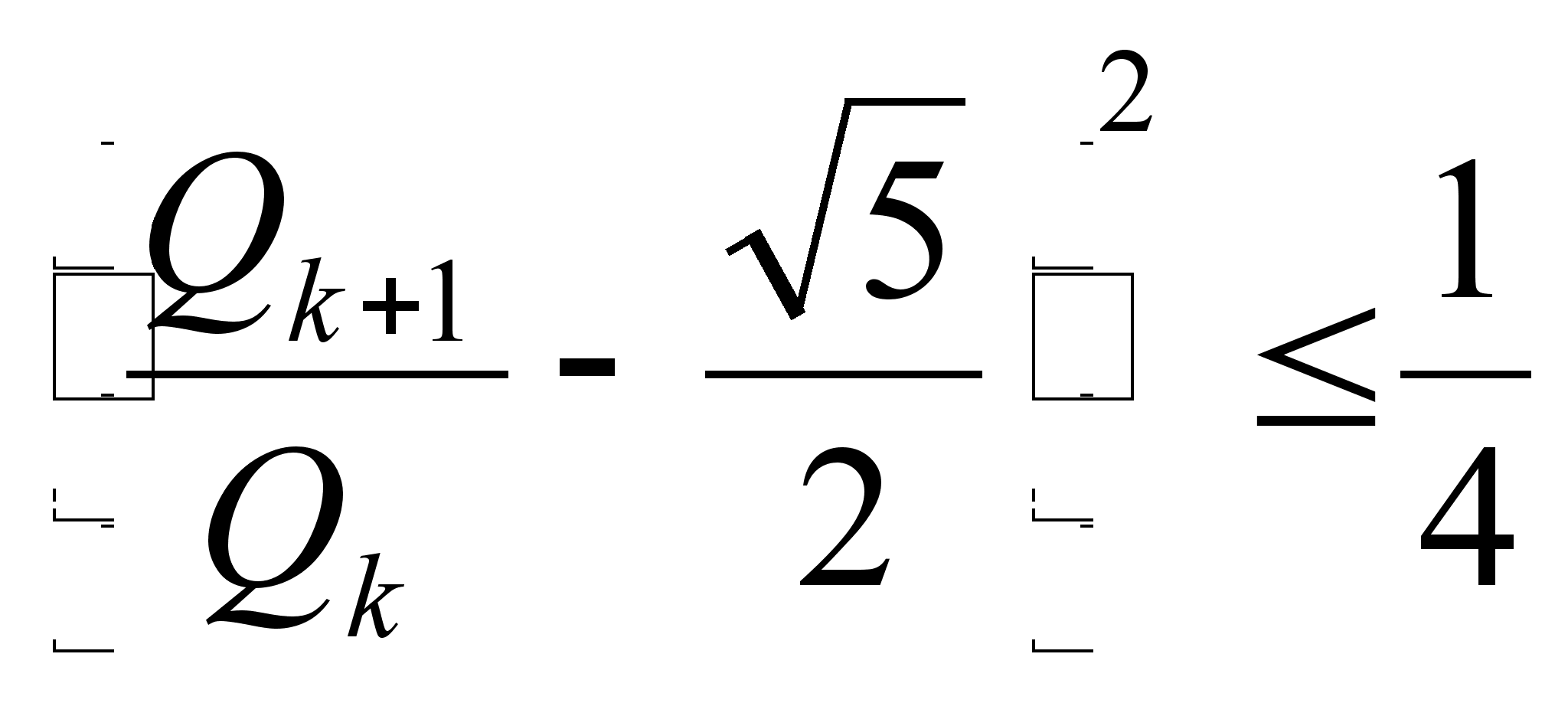 ,
,
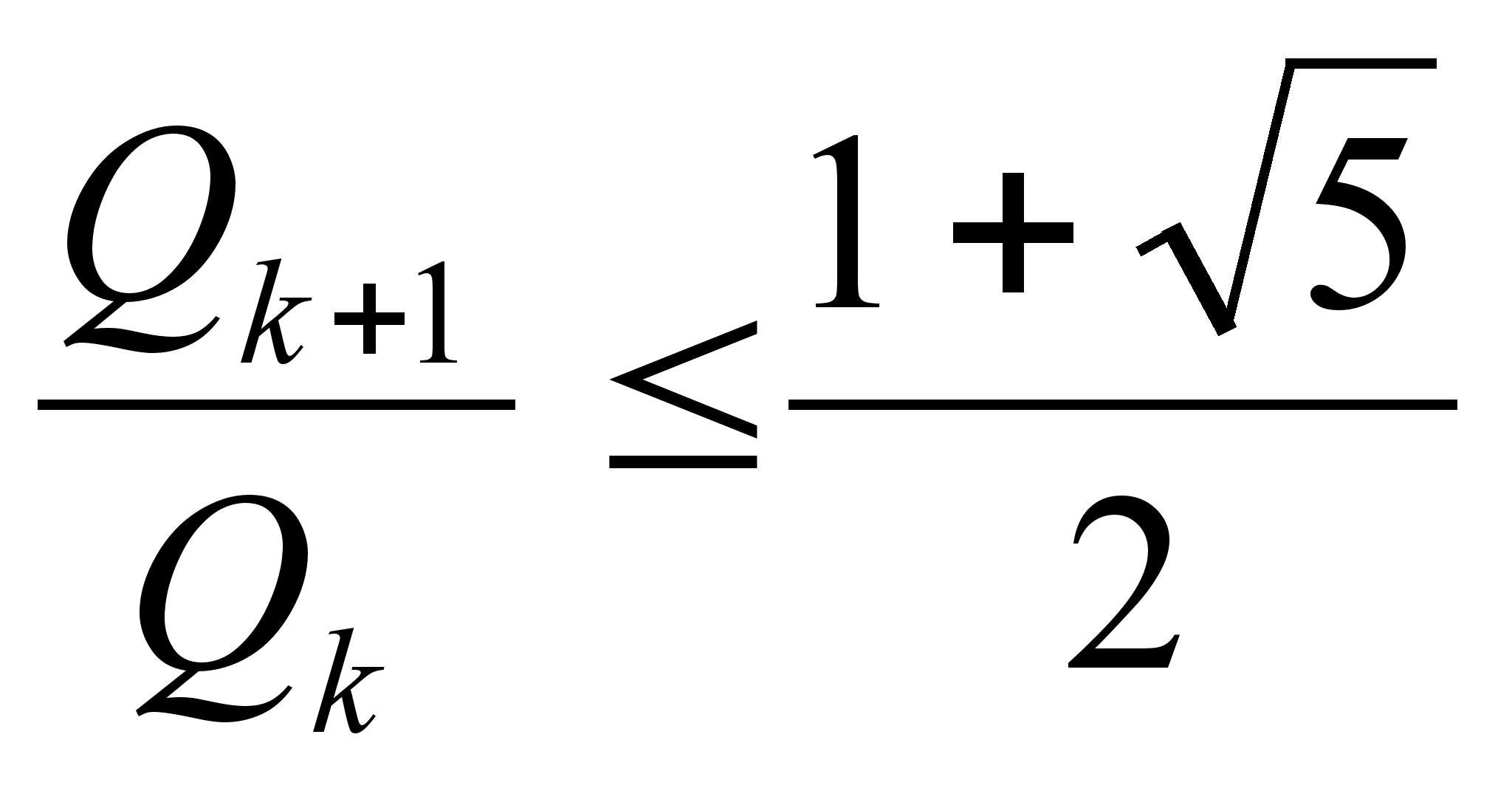 ,
или, поскольку
,
или, поскольку
![]() и
и ![]() целые,
целые,
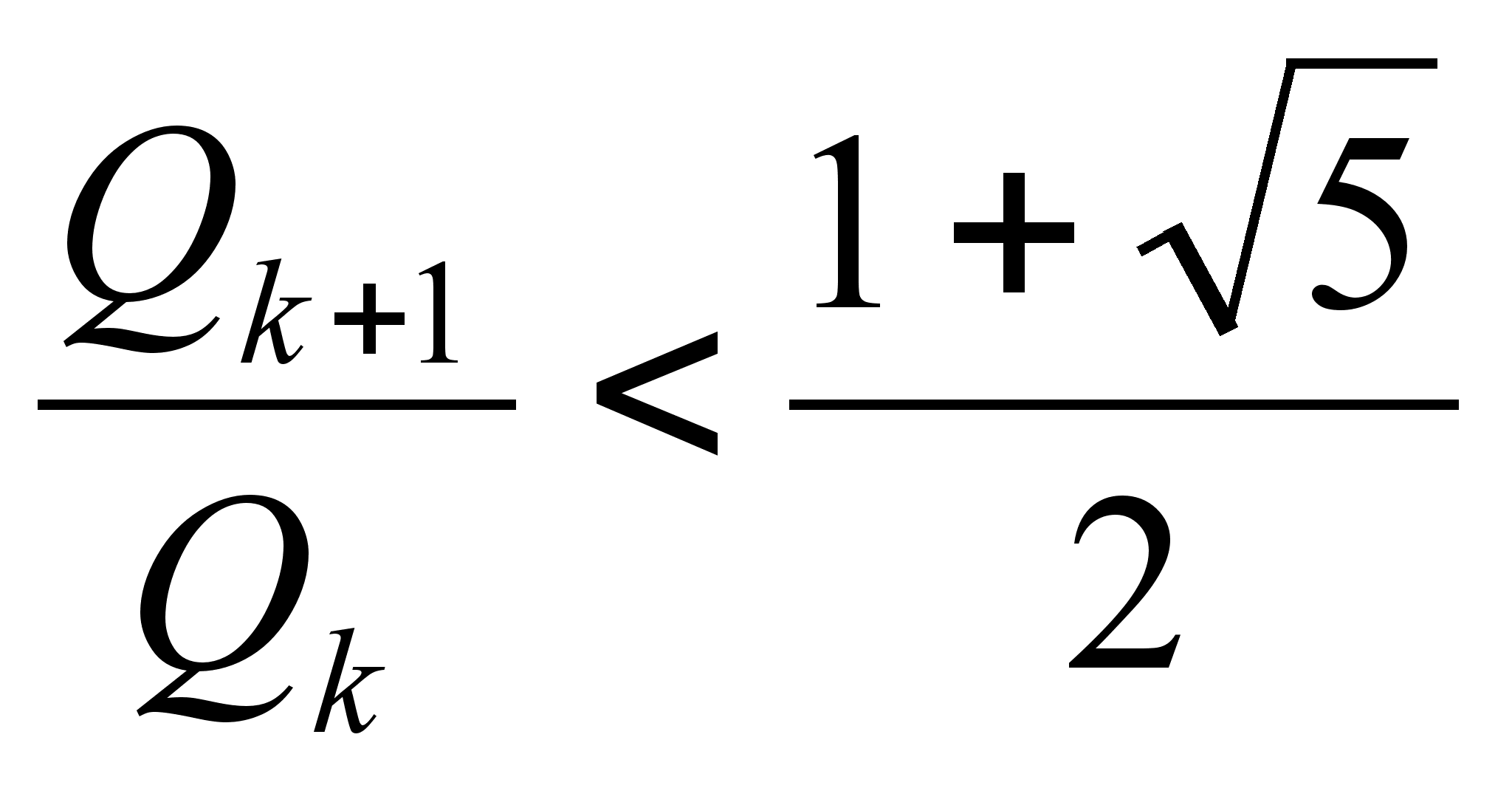 . (3)
. (3)
Так
как
![]() и
и
![]() также расположены
по разные стороны
от
также расположены
по разные стороны
от ![]() ,
из
(2) аналогично
получаем:
,
из
(2) аналогично
получаем: 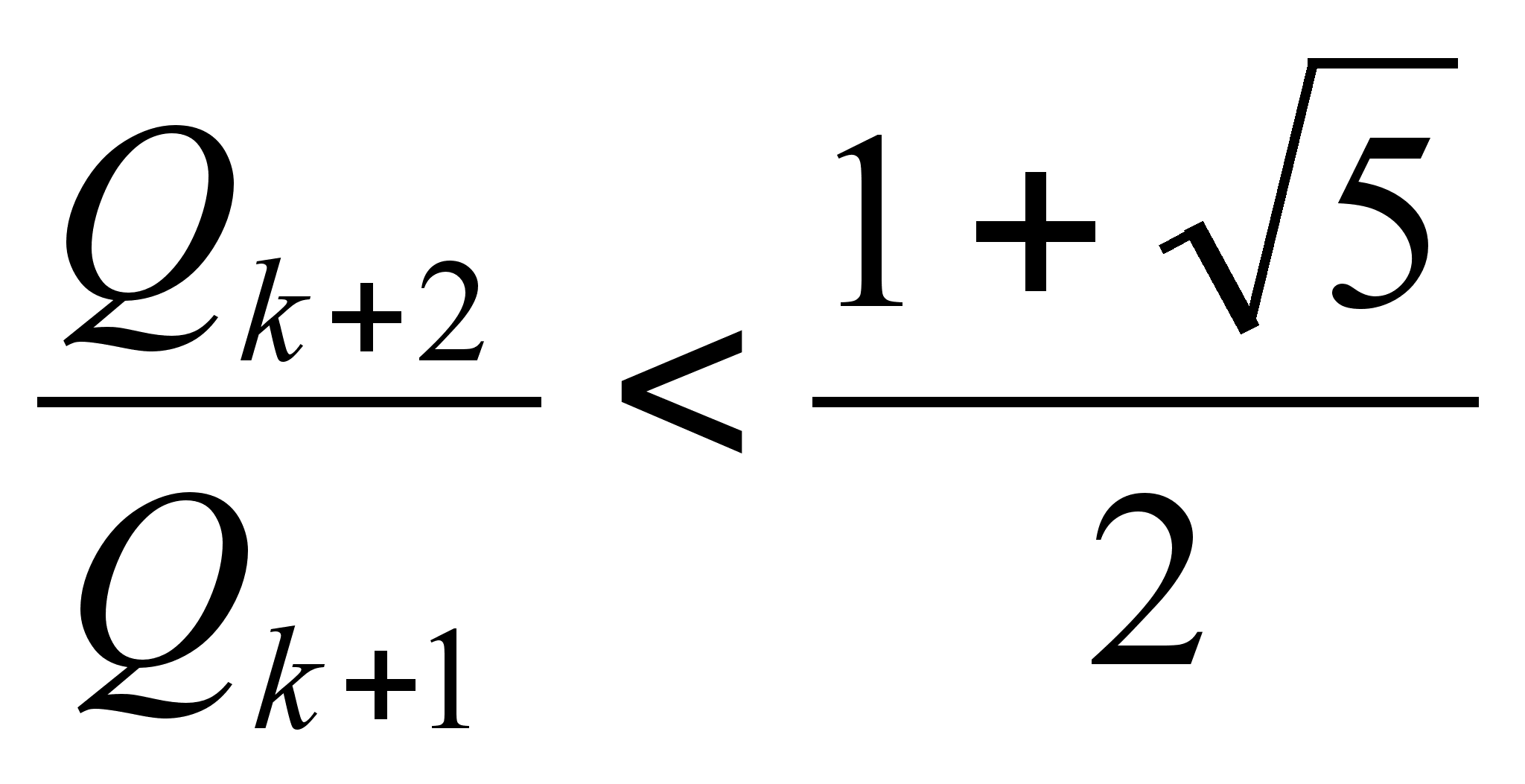 . (4)
. (4)
Пользуясь
еще тем, что
![]() из
(3) и
(4) получаем:
из
(3) и
(4) получаем:
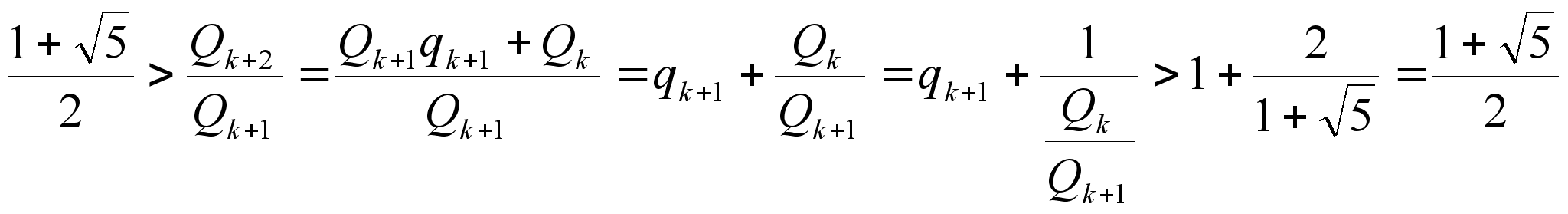 .
.
Предположение,
что выполнены
все три неравенства
(2),
привело нас
к противоречию,
поэтому по
крайней мере
для одной из
трех подходящих
дробей ![]() ,
, ![]() ,
, ![]() ,
взятой в качестве
,
взятой в качестве ![]() ,
должно выполняться
неравенство
(
,
должно выполняться
неравенство
(![]() ).
).
Придавая
k
различные
значения, получим
бесконечное
множество
дробей, удовлетворяющих
неравенству
(![]() ).
).
Докажем вторую часть.
Предположим,
что при ![]() ,
,
![]() неравенство
(1)
неравенство
(1) 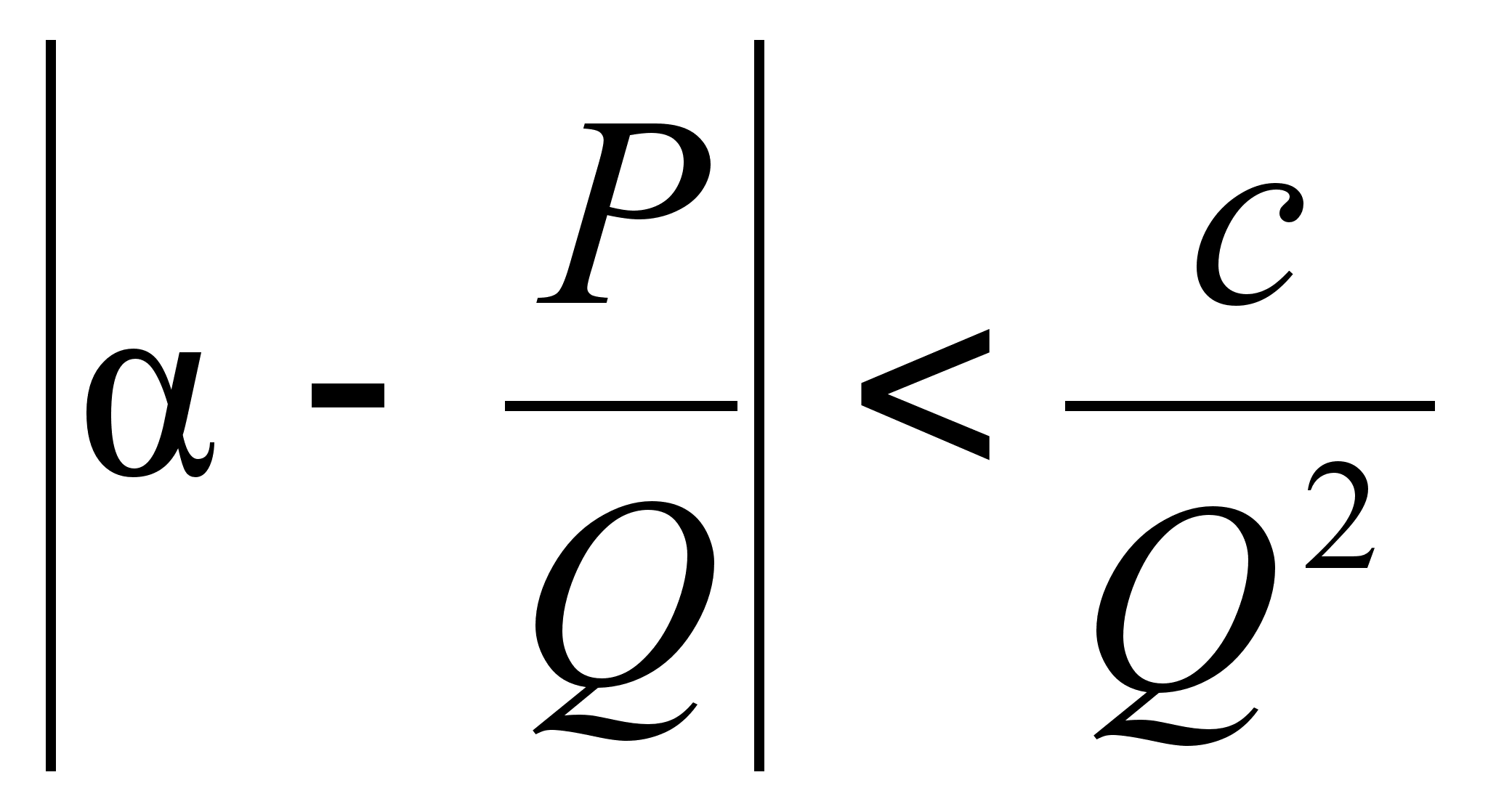 удовлетворяется
для бесконечного
множества
рациональных
чисел
удовлетворяется
для бесконечного
множества
рациональных
чисел ![]() .
Тогда для каждой
такой дроби
неравенства
.
Тогда для каждой
такой дроби
неравенства ![]() ,
откуда, подставляя
значение
,
откуда, подставляя
значение ![]() ,
получаем
,
получаем 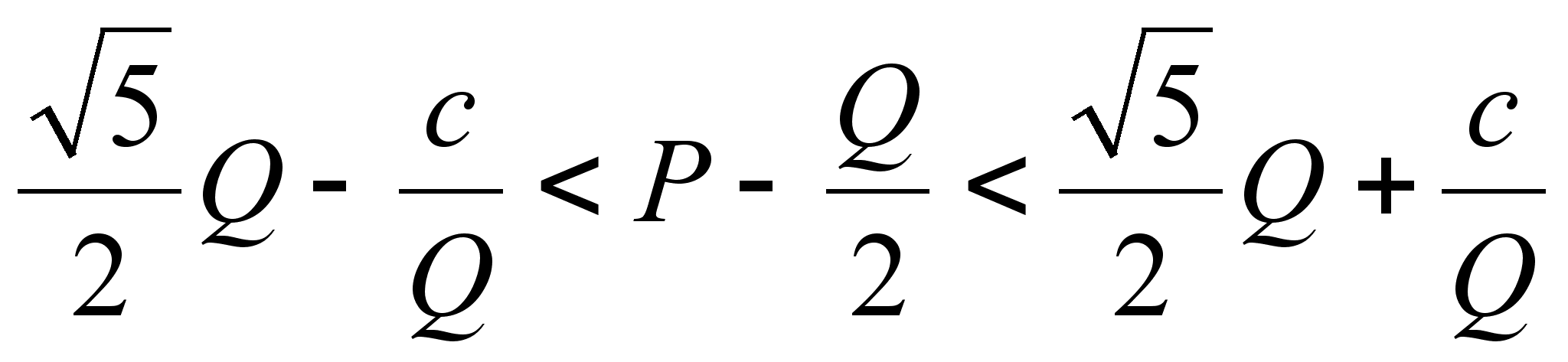 ,
а возводя в
квадрат, получаем:
,
а возводя в
квадрат, получаем: 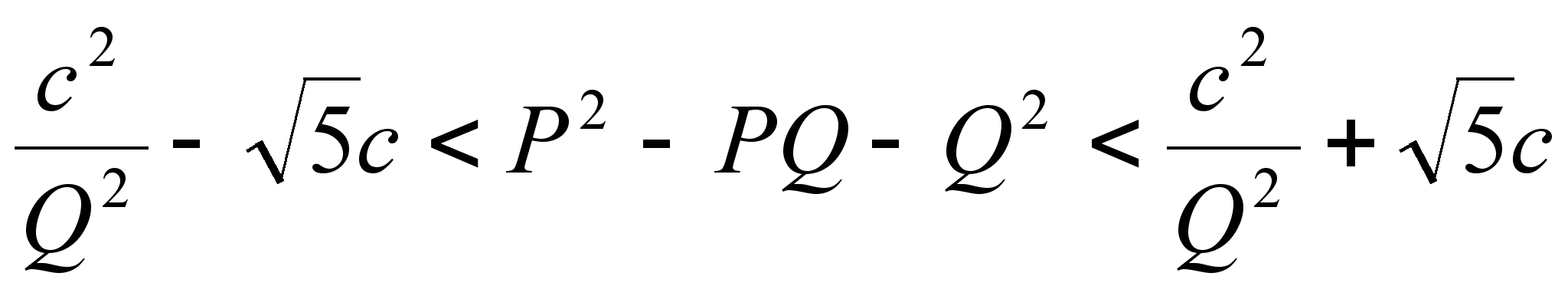 .
Так как
.
Так как ![]() ,
то при достаточно
большом
Q будем
иметь:
,
то при достаточно
большом
Q будем
иметь:
![]() и, следовательно,
целое число
и, следовательно,
целое число ![]() ,
,
![]() =
=![]() ,
что при целых
P
и
Q
не может иметь
места. Полученное
противоречие
показывает,
что неравенство
(1) может
иметь место
только для
конечного числа
рациональных
чисел
,
что при целых
P
и
Q
не может иметь
места. Полученное
противоречие
показывает,
что неравенство
(1) может
иметь место
только для
конечного числа
рациональных
чисел ![]() .
Теорема доказана
полностью.
.
Теорема доказана
полностью.
Эта теорема
была опубликована
Гурвицем в 1891
году. Тот факт,
что из трех
соседних подходящих
дробей по крайней
мере одна даст
приближение
вида 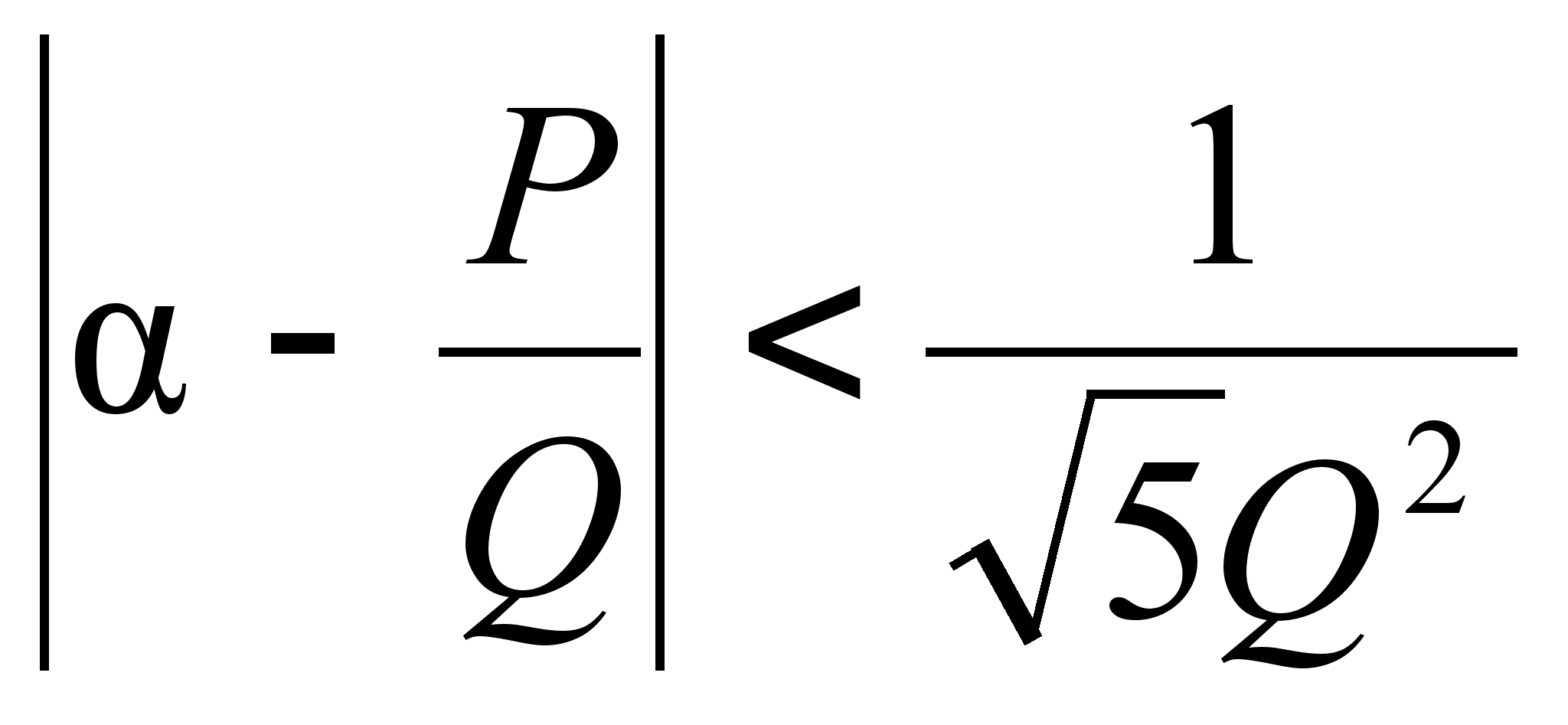 ,
был доказан
Борелем в 1903 году.
,
был доказан
Борелем в 1903 году.
Последним теоремам можно дать и другое очень важное истолкование.
Рассмотрим
для этого уравнение
![]() ,
где
,
где ![]() – любое действительное
иррациональное
число. Исключая
тривиальное
решение x=y=0,
это уравнение
не может иметь
решение в целых
числах. Однако
можно поставить
задачу о приближенном
его решении
в целых числах,
то есть о нахождении
таких пар чисел
x(x>0)
и y,
чтобы:
– любое действительное
иррациональное
число. Исключая
тривиальное
решение x=y=0,
это уравнение
не может иметь
решение в целых
числах. Однако
можно поставить
задачу о приближенном
его решении
в целых числах,
то есть о нахождении
таких пар чисел
x(x>0)
и y,
чтобы:
![]() или
или ![]() .
.
Теорема
Гурвица-Бореля
показывает,
что для
![]() всегда существует
бесконечное
множество таких
пар; если же
всегда существует
бесконечное
множество таких
пар; если же ![]() ,
то существуют
такие действительные
числа, для которых
таких пар имеется
лишь конечное
множество.
,
то существуют
такие действительные
числа, для которых
таких пар имеется
лишь конечное
множество.
Новая точка зрения получает в содружестве с методом Дирихле весьма значительное применение в теории диофантовых приближений.
§ 3. Квадратические иррациональности и периодические цепные дроби.
Рациональные
числа представляют
собой корни
уравнений
первой степени
вида
![]() с целыми коэффициентами.
с целыми коэффициентами.
Во множестве иррациональных чисел наиболее простыми являются те иррациональности, которые являются корнями квадратных уравнений с целыми коэффициентами; такие числа будем называть квадратическими иррациональностями.
Число ![]() называется
квадратической
иррациональностью,
если
называется
квадратической
иррациональностью,
если ![]() – иррациональный
корень некоторого
уравнения
– иррациональный
корень некоторого
уравнения
![]() (1) с
целыми коэффициентами,
не равными
одновременно
нулю.
(1) с
целыми коэффициентами,
не равными
одновременно
нулю.
При таком
![]() ,
очевидно, будет
a
,
очевидно, будет
a![]() 0,
c
0,
c![]() 0.
Коэффициенты
a,
b,
c
уравнения (1),
очевидно, можно
взять взаимно
простыми; в
этом случае
дискриминант
этого уравнения
0.
Коэффициенты
a,
b,
c
уравнения (1),
очевидно, можно
взять взаимно
простыми; в
этом случае
дискриминант
этого уравнения
![]() будем называть
также дискриминантом
будем называть
также дискриминантом
![]() .
Корни уравнения
(1) равны
.
Корни уравнения
(1) равны
![]() и
и ![]() ,
так что любую
квадратическую
иррациональность
,
так что любую
квадратическую
иррациональность ![]() можно представить
в виде
можно представить
в виде 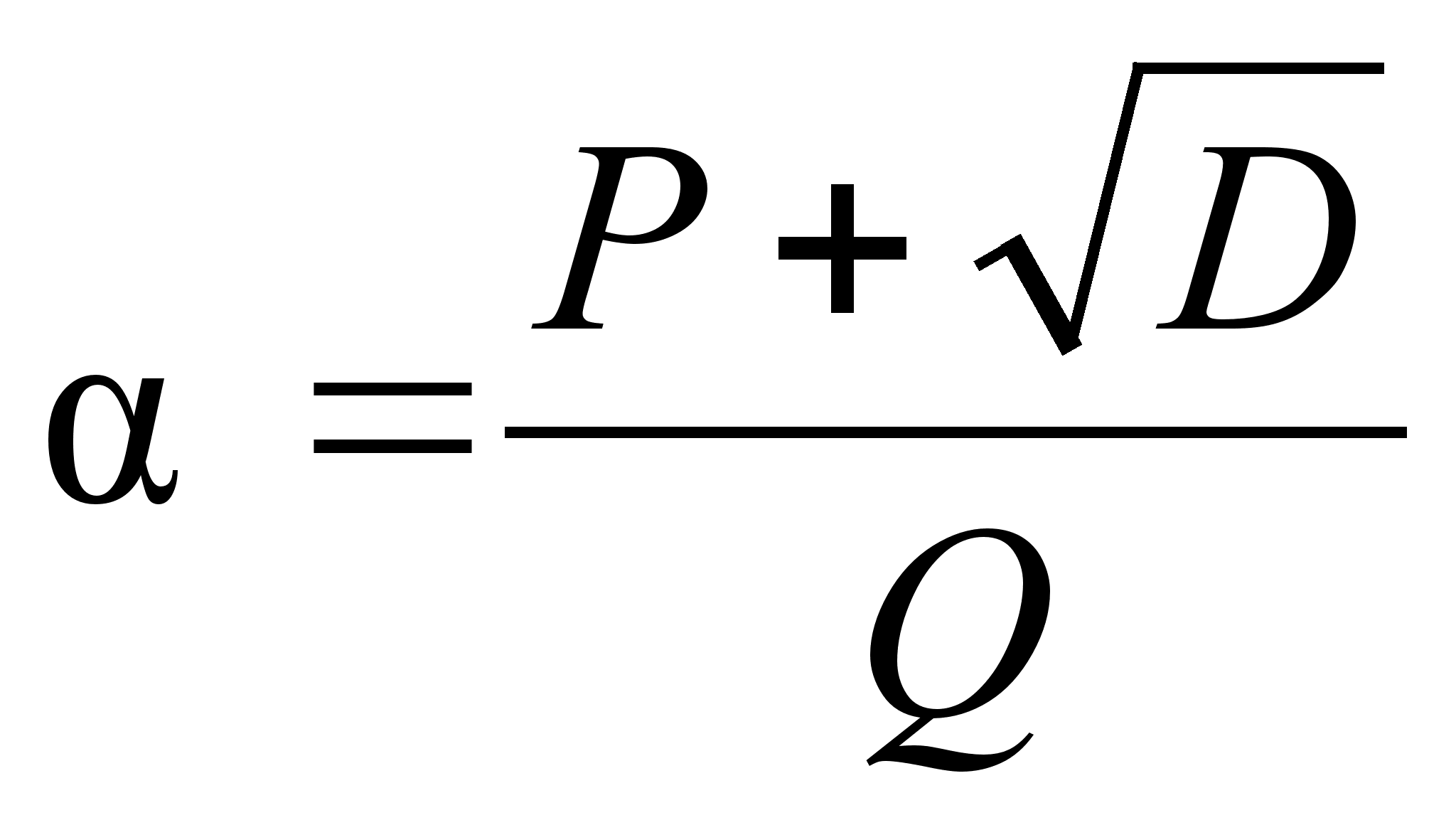 ,
где
P,
Q
– целые, а
D
(D>1)
– целое неквадратное
число.
,
где
P,
Q
– целые, а
D
(D>1)
– целое неквадратное
число.
Второй
корень уравнения
(1) 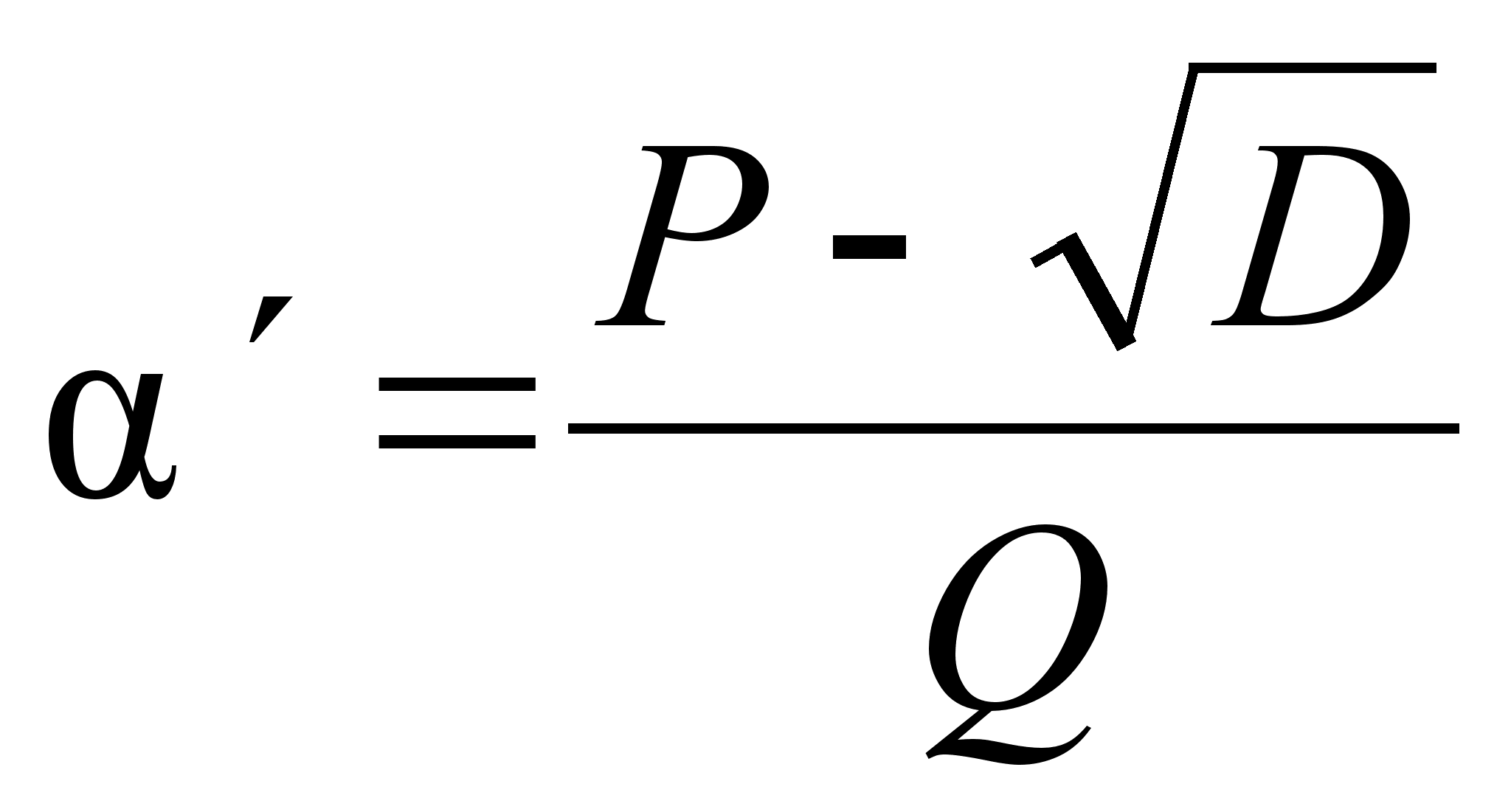 будем называть
иррациональностью,
сопряженной
с
будем называть
иррациональностью,
сопряженной
с ![]() .
.
В определении
квадратической
иррациональности
особенно важно
обратить внимание
на то, что речь
идет о квадратных
уравнениях
с целыми коэффициентами.
Любое ![]() является корнем
квадратного
уравнения и
даже уравнения
первой степени,
например уравнений
является корнем
квадратного
уравнения и
даже уравнения
первой степени,
например уравнений
![]() ,
x-
,
x-![]() =0.
=0.
Примеры:
![]() – квадратическая иррациональность, так как
– квадратическая иррациональность, так как ![]() является иррациональным корнем уравнения
является иррациональным корнем уравнения ![]() .
.
![]() – квадратическая иррациональность, так как
– квадратическая иррациональность, так как ![]() представляет собой иррациональный корень уравнения
представляет собой иррациональный корень уравнения ![]() . Здесь P=–1, Q=–3, D=5.
. Здесь P=–1, Q=–3, D=5.
![]() не является квадратической иррациональностью.
не является квадратической иррациональностью.
Действительно,
корень любого
квадратного
уравнения с
целыми коэффициентами
имеет вид 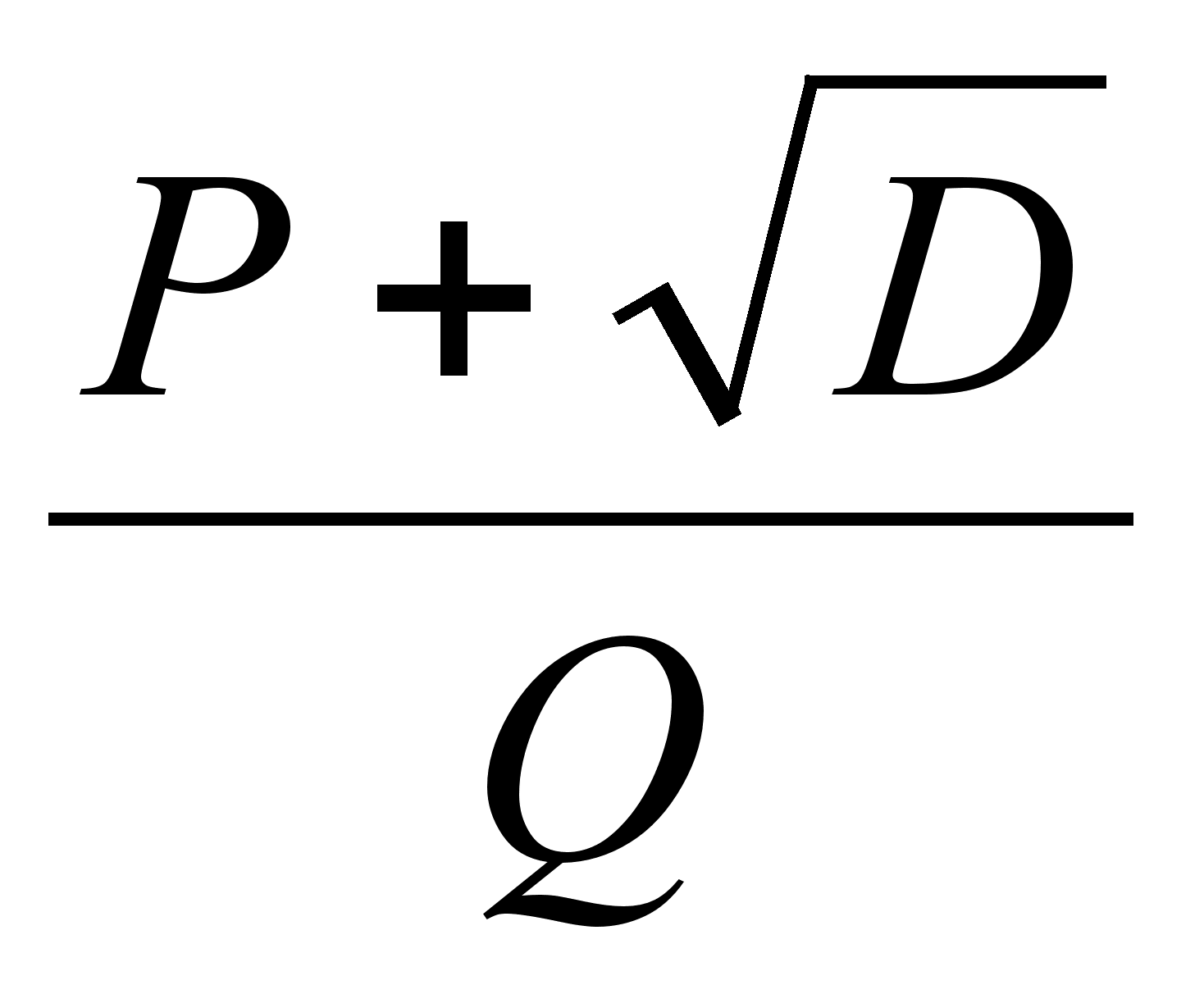 ,
где P,
Q,
D
,
где P,
Q,
D![]() ,
причем D>1.
Если бы мы имели
,
причем D>1.
Если бы мы имели ![]() =
=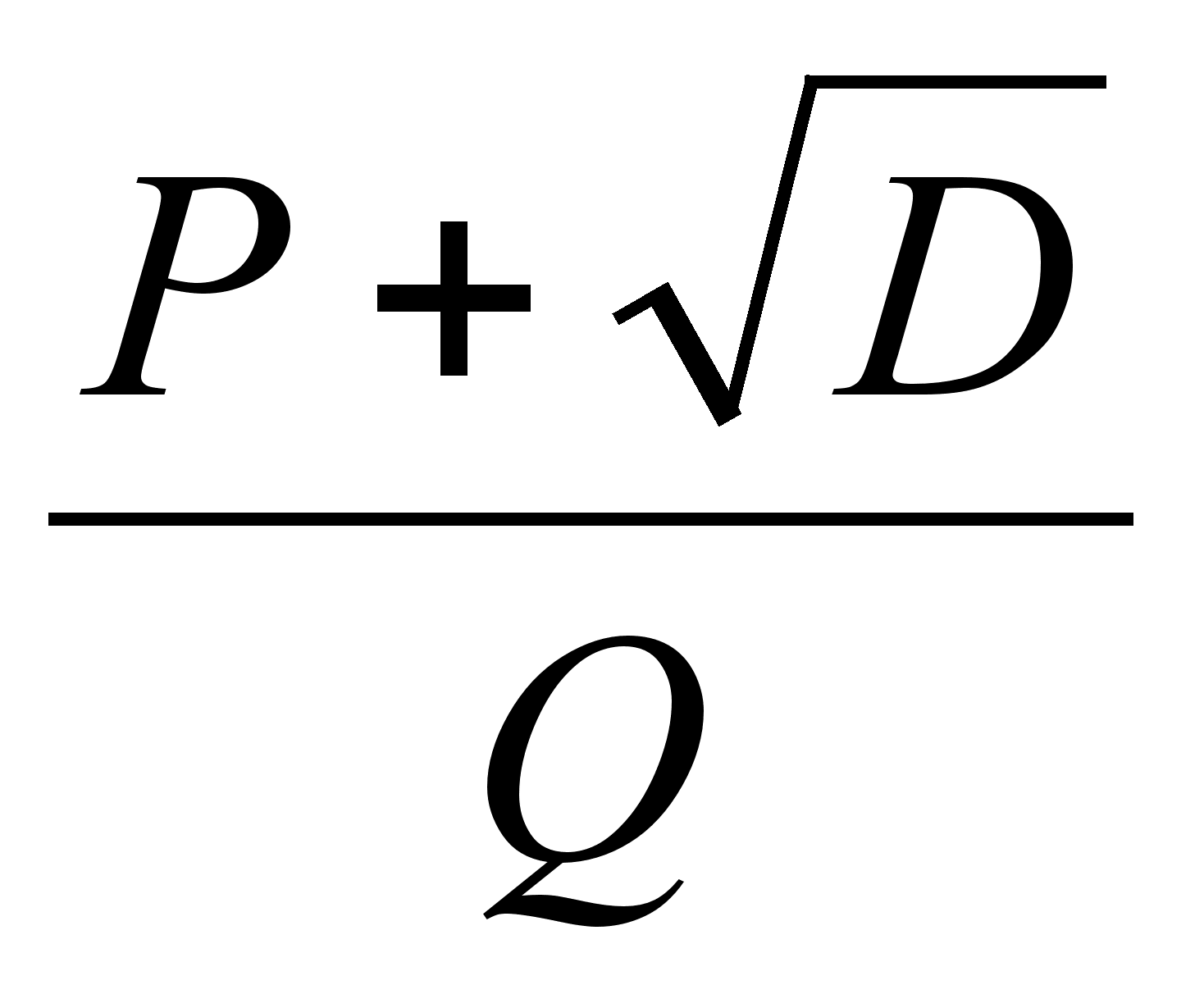 ,
то, возводя это
равенство в
куб, мы получили
бы, что
,
то, возводя это
равенство в
куб, мы получили
бы, что
![]() – рациональное
число, а следовательно,
рациональным
являлся бы и
– рациональное
число, а следовательно,
рациональным
являлся бы и ![]() ,
а это не так.
,
а это не так.
Теорема: Всякая периодическая непрерывная дробь изображает квадратическую иррациональность.
Доказательство:
Пусть ![]() –
смешанная
периодическая
цепная дробь,
то есть
–
смешанная
периодическая
цепная дробь,
то есть ![]() ,
где
,
где ![]() – чисто периодическая
цепная дробь.
– чисто периодическая
цепная дробь.
Обозначим
подходящие
дроби к ![]() и
и ![]() соответственно
через
соответственно
через
![]() и
и ![]() .
.
Так
как ![]() ,
то,
согласно формуле
(5) из 1.1 этой главы,
,
то,
согласно формуле
(5) из 1.1 этой главы, ![]() .
Выполнив необходимые
преобразования,
получаем:
.
Выполнив необходимые
преобразования,
получаем:
![]() .
.
Из
этой формулы
видно, что ![]() удовлетворяет
квадратному
уравнению с
целыми коэффициентами.
Кроме того,
удовлетворяет
квадратному
уравнению с
целыми коэффициентами.
Кроме того, ![]() - число иррациональное,
так как оно
представляет
бесконечную
непрерывную
дробь. Таким
образом,
- число иррациональное,
так как оно
представляет
бесконечную
непрерывную
дробь. Таким
образом, ![]() - квадратическая
иррациональность.
Но по той же
формуле
- квадратическая
иррациональность.
Но по той же
формуле ![]() ,
поэтому и
,
поэтому и ![]() является, очевидно,
квадратической
иррациональностью,
что и требовалось
доказать.
является, очевидно,
квадратической
иррациональностью,
что и требовалось
доказать.
Докажем обратную теорему, которая носит имя Лагранжа.
Теорема Лагранжа: Всякая действительная квадратическая иррациональность изображается периодической непрерывной дробью.
Доказательство:
Пусть ![]() – действительный
иррациональный
корень квадратного
уравнения
– действительный
иррациональный
корень квадратного
уравнения
![]() (1) с
целыми коэффициентами
a,
b,
c.
(1) с
целыми коэффициентами
a,
b,
c.
При
разложении ![]() в непрерывную
дробь получаем
в непрерывную
дробь получаем ![]() (2), где
(2), где ![]() – остаток
– остаток ![]() порядка k+1.
порядка k+1.
Подставляя
выражение ![]() из
(2) в
(1),
получаем
из
(2) в
(1),
получаем
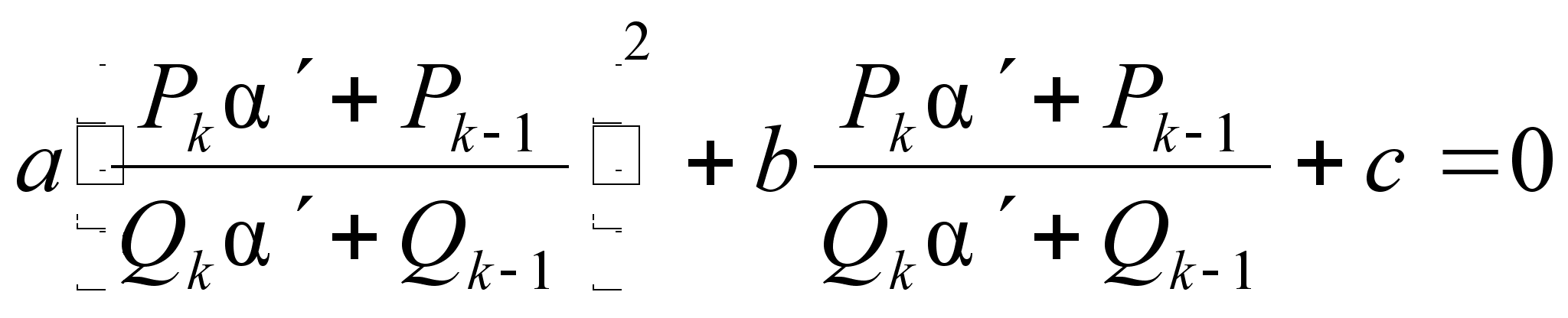
![]()
![]()
![]()
![]()
![]()
![]() (3),
где
(3),
где
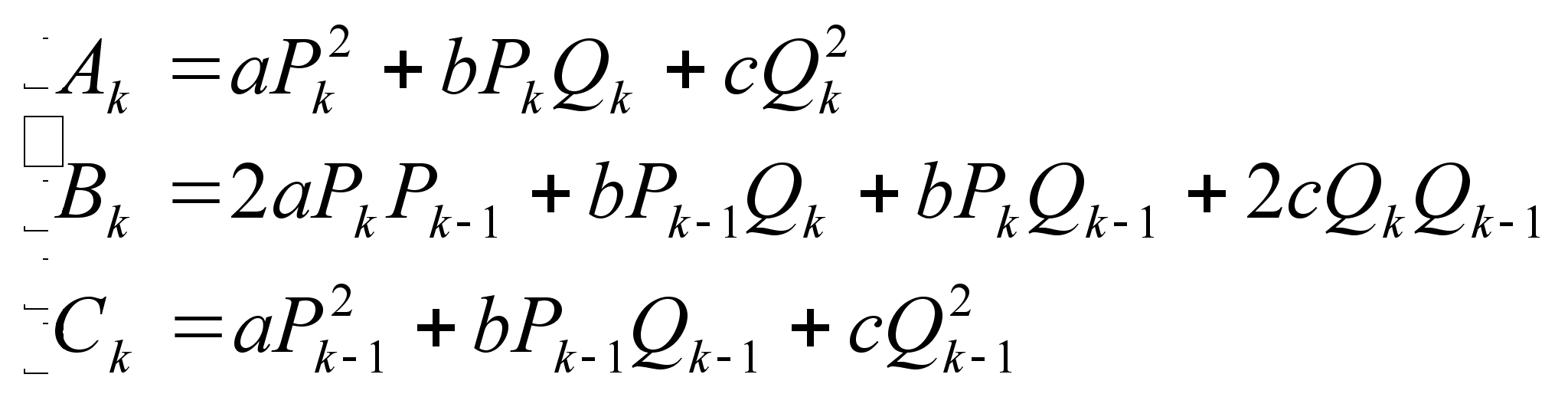 (4)
(4)
Отсюда,
во-первых, видно,
что ![]() (5), во-вторых,
можно непосредственным
вычислением
установить,
что
(5), во-вторых,
можно непосредственным
вычислением
установить,
что ![]() (6).
(6).
Таким образом, дискриминант уравнения (3) такой же, как и дискриминант уравнения (1), откуда следует, что он от k не зависит.
Идея
доказательства
в дальнейшем
заключается
в том, чтобы
показать, что
при данном ![]() коэффициенты
коэффициенты
![]() ,
,
![]() ,
,
![]() ограничены
по модулю.
ограничены
по модулю.
Если
этот факт на
самом деле имел
бы место, то
это означало
бы, что коэффициенты,
будучи целыми
числами, могут
принимать
только конечное
число различных
значений. Вместе
с тем и число
возможных
уравнений
(3) было
бы конечным,
хотя
k
пробегает
бесконечное
множество
значений. Но
в таком случае
и остатки ![]() (которые определяются
из (3)),
число которых
бесконечно,
могли бы принять
только конечное
число различных
значений. Поэтому
должны были
бы существовать
остатки
(которые определяются
из (3)),
число которых
бесконечно,
могли бы принять
только конечное
число различных
значений. Поэтому
должны были
бы существовать
остатки ![]() с одинаковыми
значениями,
а это уже означает,
что непрерывная
дробь – периодическая.
с одинаковыми
значениями,
а это уже означает,
что непрерывная
дробь – периодическая.
Итак,
докажем, что
![]() ,
,
![]() и
и
![]() ограничены
по абсолютной
величине. Достаточно
сделать это
для
ограничены
по абсолютной
величине. Достаточно
сделать это
для ![]() ,
так как в силу
соотношения
(5),
из ограниченности
,
так как в силу
соотношения
(5),
из ограниченности
![]() уже как следствие
вытекает
ограниченность
уже как следствие
вытекает
ограниченность ![]() ,
а в силу
(6) –
ограниченность
,
а в силу
(6) –
ограниченность ![]() .
.
Как
известно из
свойств подходящих
дробей,
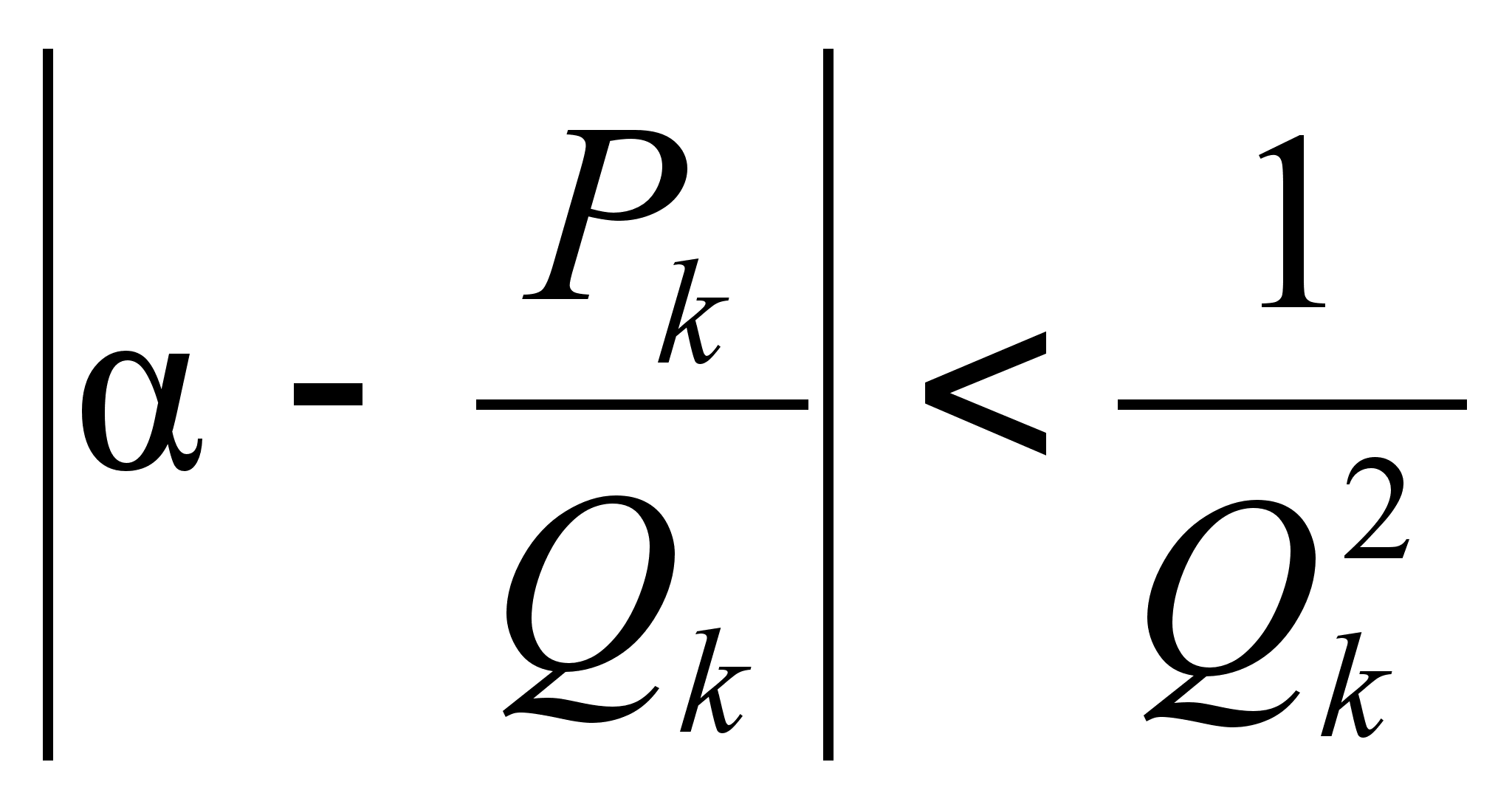 или
или ![]() ,
где
,
где ![]() ,
откуда
,
откуда ![]() .
.
Поэтому из первого равенства (4) имеем
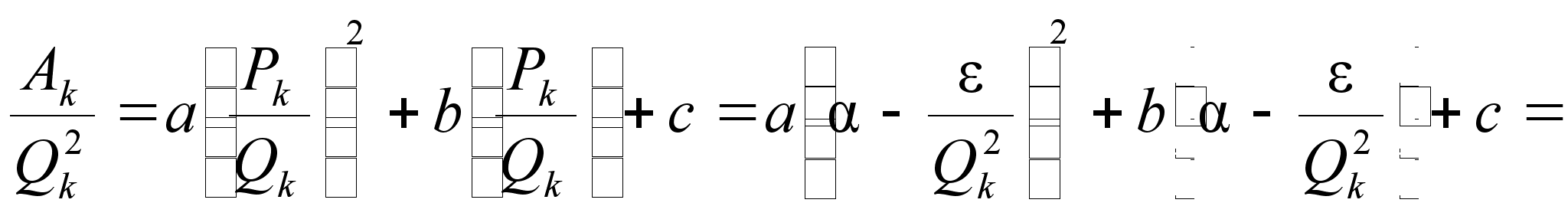
![]()
Так
как ![]() ,
то
,
то
![]()
![]() ,
,
то
есть
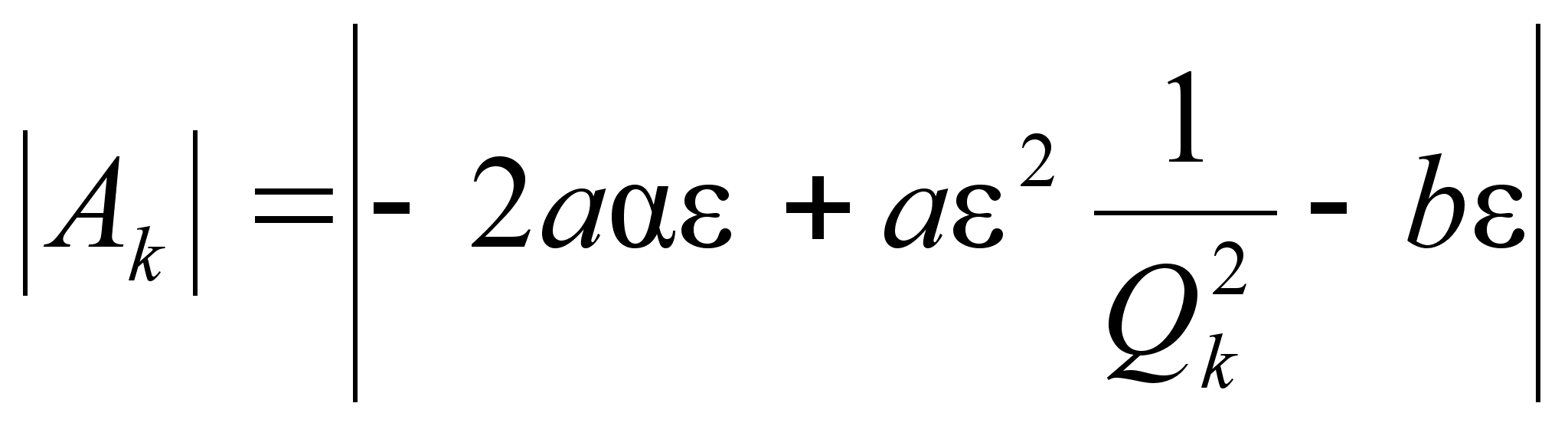 и
и ![]() ,
а это и доказывает
ограниченность
,
а это и доказывает
ограниченность ![]() .
.
Этим и завершается доказательство теоремы Лагранжа.
Отметим без доказательства следующие свойства разложений квадратических иррациональностей:
при разложении квадратного корня и целого положительного числа, не являющегося полным квадратом, период начинается со второго звена;
чисто периодическая цепная дробь получается тогда и только тогда, когда квадратическая иррациональность больше 1, а сопряженная иррациональность лежит в интервале (-1; 0) (это свойство было доказано Э. Галуа в 1828 году. Он доказал также, что в случае чисто периодического разложения сопряженная квадратическая иррациональность имеет те же элементы, но расположенные в обратном порядке).
Примеры:
Составить уравнение, один из корней которого разлагается в периодическую цепную дробь x и найти соответствующую иррациональность x=((2, 6, 1)).
Решение: x=(2, 6, 1, x).
Составляем схему вычисления числителей и знаменателей подходящих дробей.
| 2 | 6 | 1 | x | |
| 1 | 2 | 13 | 15 | 15x+13 |
| 0 | 1 | 6 | 7 | 7x+6 |
Итак, ![]() ,
откуда получаем:
,
откуда получаем:
![]()
![]() .
.
Положительное решение этого уравнения дает искомую периодическую дробь.
((2, 6,
1))=![]() - квадратическая
иррациональность.
Заметим, что
- квадратическая
иррациональность.
Заметим, что ![]() >1,
а
>1,
а
![]() – иррациональность,
сопряженная
с
x
– лежит в интервале
(-1;
0).
– иррациональность,
сопряженная
с
x
– лежит в интервале
(-1;
0).
Составить уравнение, один из корней которого разлагается в периодическую цепную дробь x=(3, (2, 1)) и найти соответствующую иррациональность.
Решение x=(3, y), где y=(2, 1, y). Составляем схему для вычисления числителей и знаменателей подходящих дробей y:
| 2 | 1 | y | |
| 1 | 2 | 3 | 3y+2 |
| 0 | 1 | 1 | y+1 |
Следовательно, ![]() ,
,
![]()
![]()
![]() .
Так как y>0,
то мы должны
взять положительный
корень этого
уравнения
.
Так как y>0,
то мы должны
взять положительный
корень этого
уравнения ![]() .
Поэтому для
x
имеем
.
Поэтому для
x
имеем
![]()
![]() .
Таким образом,
искомая дробь
(3,
(2, 1))=
.
Таким образом,
искомая дробь
(3,
(2, 1))=![]() .
Для соответствующего
квадратного
уравнения имеем
.
Для соответствующего
квадратного
уравнения имеем
![]() ,
откуда получаем:
,
откуда получаем:
![]()
![]()
![]()
![]()
![]() .
.
§4. Представление действительных чисел цепными дробями общего вида.
Рассмотренные до сих пор правильные бесконечные и конечные цепные дроби являются частным случаем бесокнечных и конечных цепных дробей общего вида:
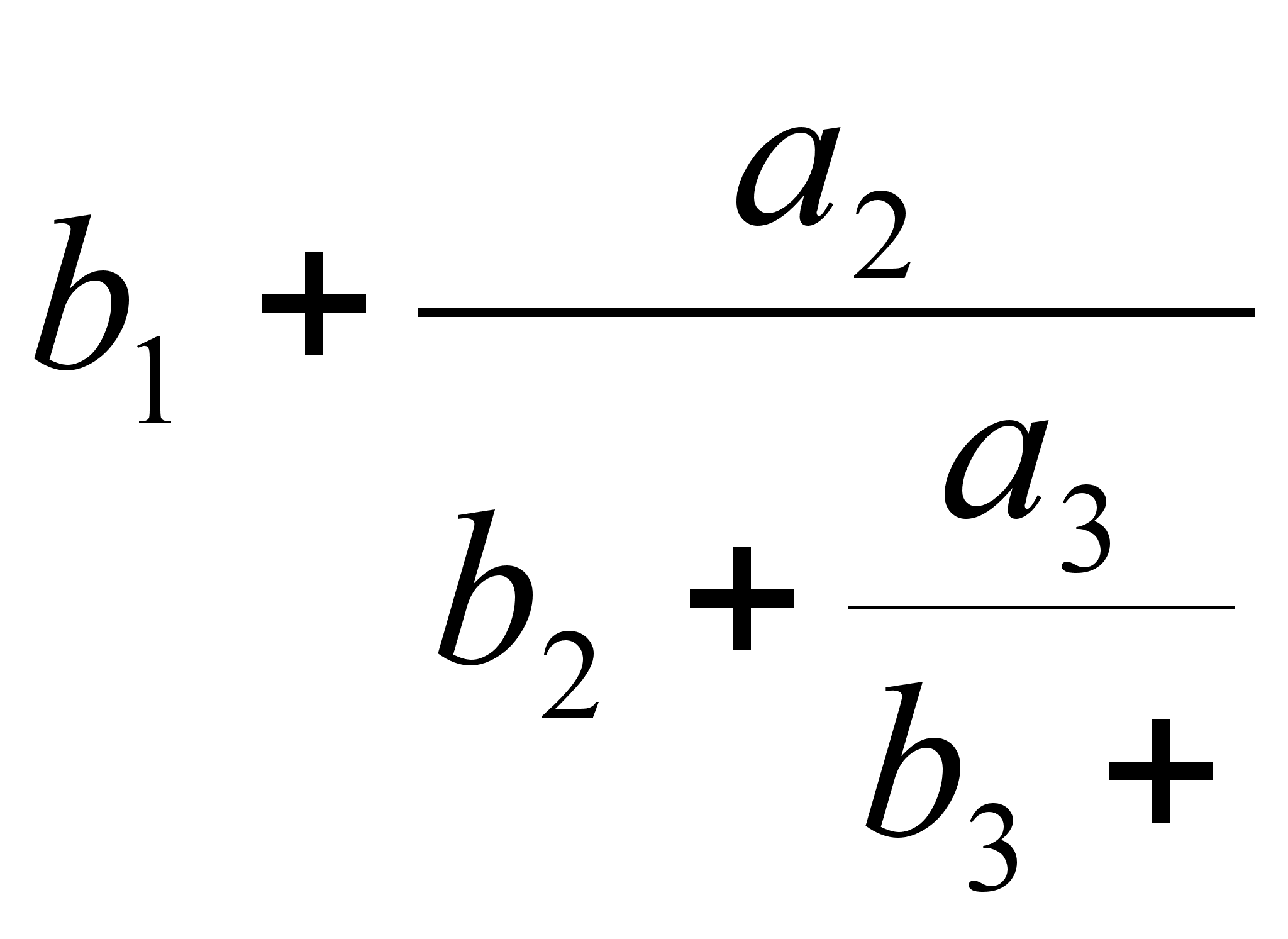 (1),
(1),
![]()
когда
в них принимается,
что все ![]() ,
,
![]() ,
а остальные
,
а остальные
![]() .
.
В общем
случае элементы
цепной дроби
![]() и
и ![]() ,
k>1
могут принимать
произвольные,
отличные от
0 рациональные
значения, а
,
k>1
могут принимать
произвольные,
отличные от
0 рациональные
значения, а
![]() может также
быть равно
нулю.
может также
быть равно
нулю.
При помощи
цепных дробей
общего вида
одно и то же
рациональное
число можно
представить
различными
способами.
Например, 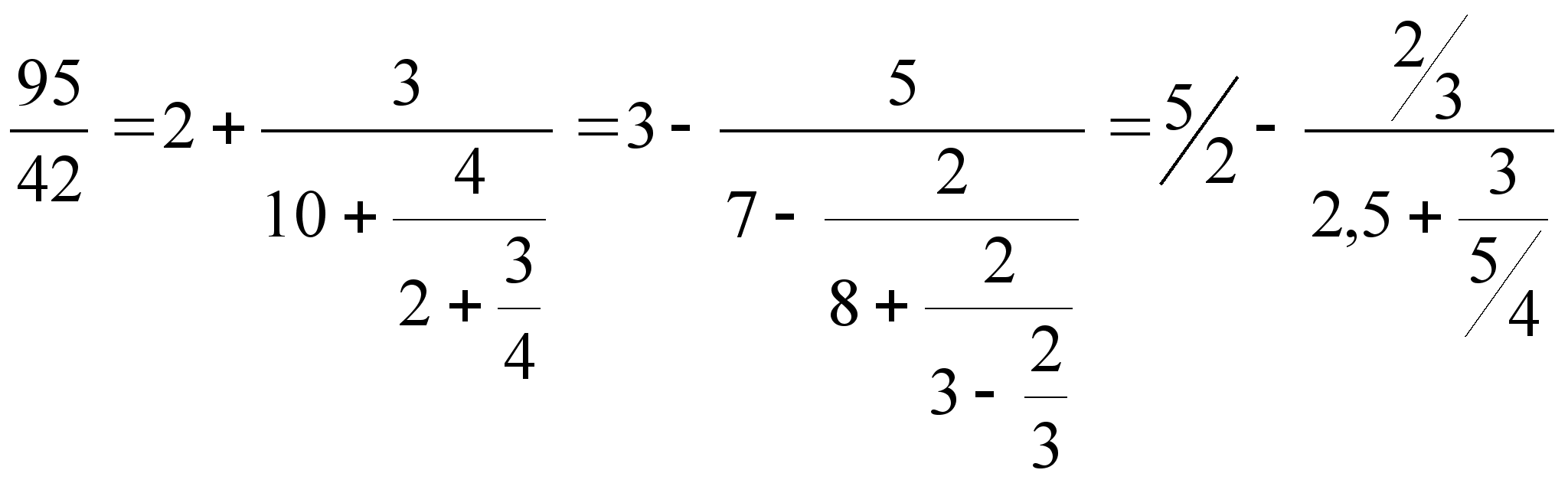 .
.
В цепной
дроби (1),
которую записывают
также иначе,
например, ![]() (
(![]() )
или
)
или 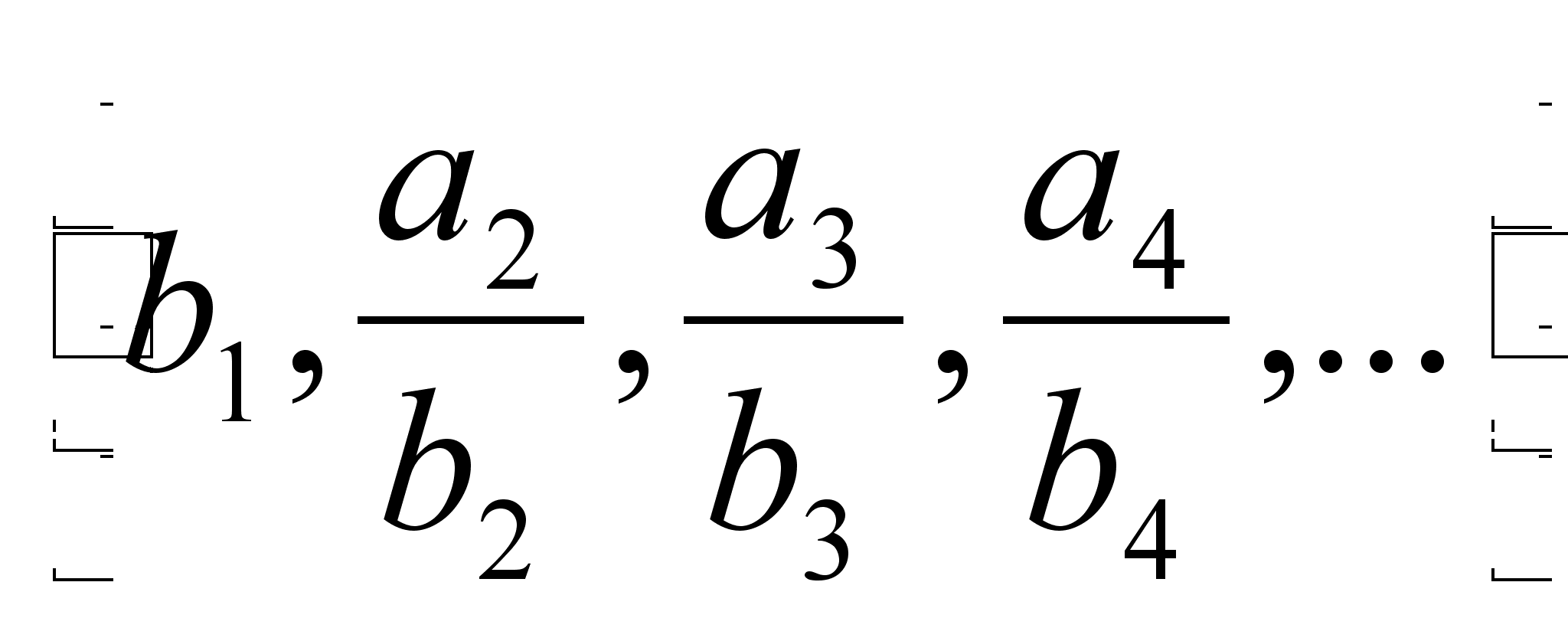 (
(![]() )
числа
)
числа
![]() и
и
![]() (k=2,
3, …)
называют звеньями,
(k=2,
3, …)
называют звеньями,
![]() и
и ![]() – членами
k–го
звена, из них
– членами
k–го
звена, из них
![]() – частным числителем,
а
– частным числителем,
а
![]() – частным
знаменателем.
– частным
знаменателем.
Чтобы
получить разложение
рационального
числа
![]() в конечную
цепную дробь
(1),
можно все
в конечную
цепную дробь
(1),
можно все
![]() и
и ![]() ,
за исключением
одного, выбрать
произвольно.
,
за исключением
одного, выбрать
произвольно.
Можно,
например, найти
разложение
![]() ;
для этого следует
положить
;
для этого следует
положить ![]() .
Можно цепную
дробь преобразовать
так, чтобы все
.
Можно цепную
дробь преобразовать
так, чтобы все
![]() были равны 1,
то есть, чтобы
(1) приняло
вид
были равны 1,
то есть, чтобы
(1) приняло
вид ![]() (2).
(2).
Так,
например, 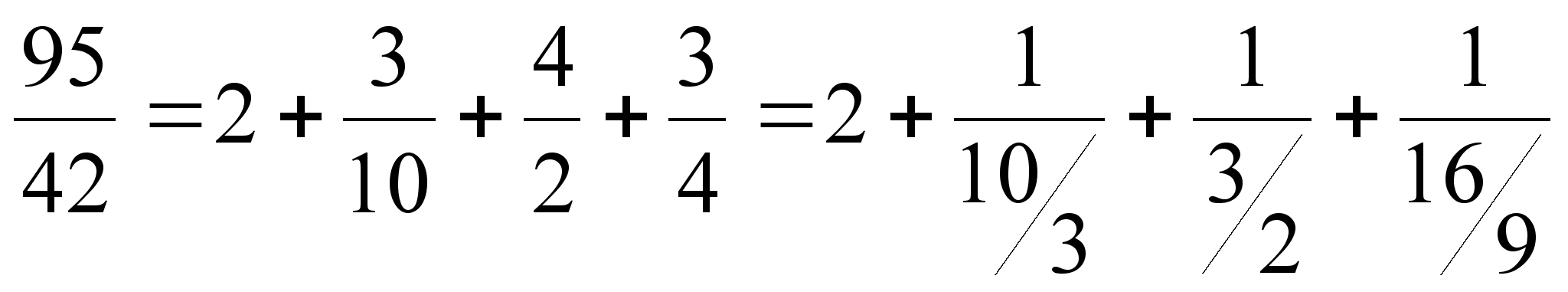 .
Дроби вида
(2) называют
обыкновенными
цепными дробями,
а
.
Дроби вида
(2) называют
обыкновенными
цепными дробями,
а
![]() ,
,
![]() ,
…,
,
…, ![]() – их неполными
частными. Правильные
цепные дроби
можно поэтому
определить
как обыкновенные
цепные дроби
с целыми положительными
неполными
частными, начиная
с
– их неполными
частными. Правильные
цепные дроби
можно поэтому
определить
как обыкновенные
цепные дроби
с целыми положительными
неполными
частными, начиная
с ![]() ,
причем
,
причем
![]() может быть
любым целым
числом.
может быть
любым целым
числом.
Правильные цепные дроби являются наиболее простыми и наиболее изученными среди цепных дробей общего вида, однако и другие цепные дроби играют большую роль и имеют важные применения, например, в приближенном анализе, где при их помощи без сложных выкладок получают дробно-рациональные приближения функций.
Рассмотрим обзорно некоторые свойства цепных дробей общего вида.
Происхождение таких цепных дробей связано с обобщенным алгоритмом Евклида.
Если
мы имеем систему
равенств
![]() ,
,
![]() ,
,
![]() ,
… с
произвольными
рациональными
числами, то при
b,
c,
d
,
… с
произвольными
рациональными
числами, то при
b,
c,
d![]() 0,
из них следуют
равенства
0,
из них следуют
равенства 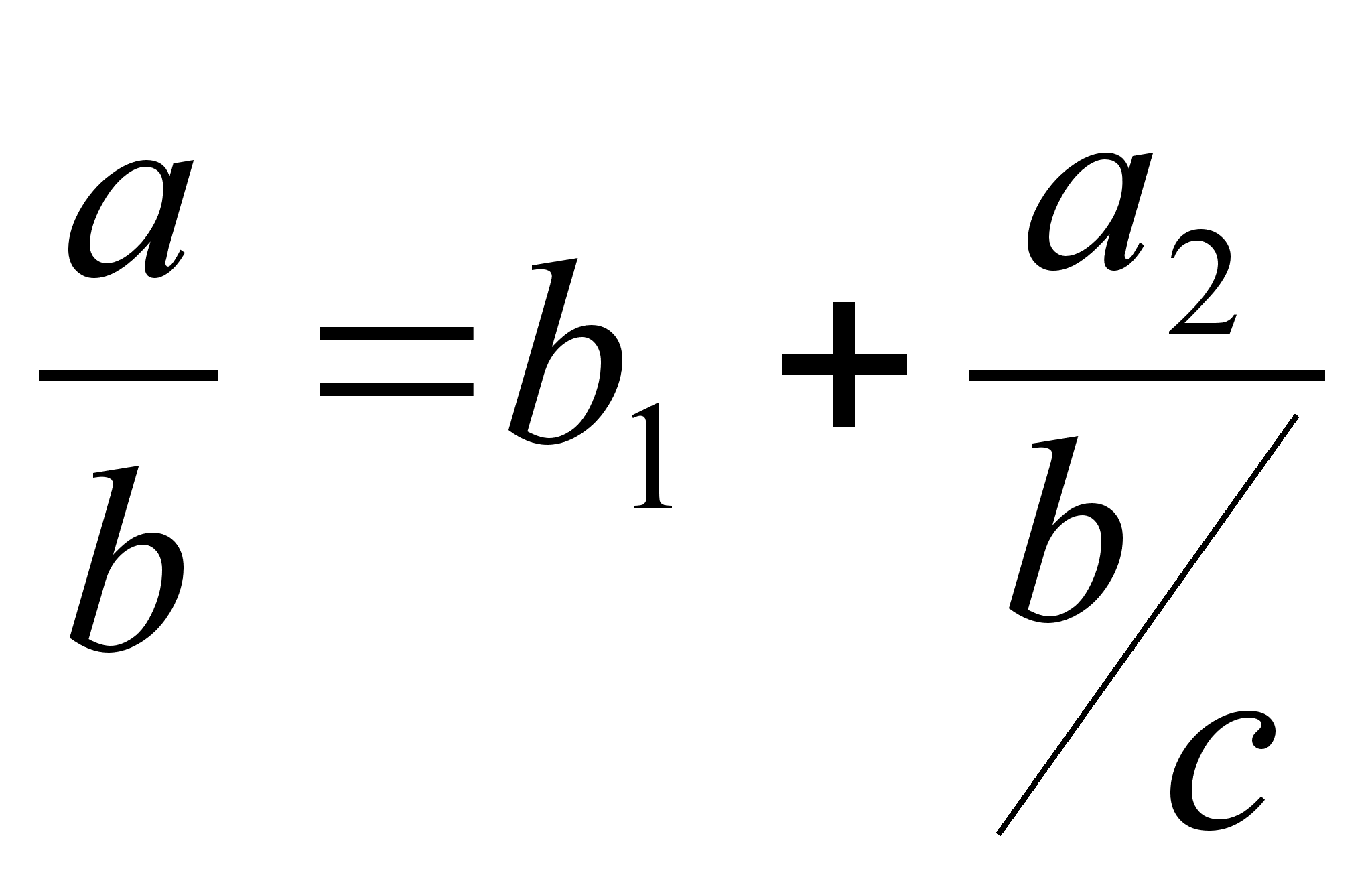 ,
, 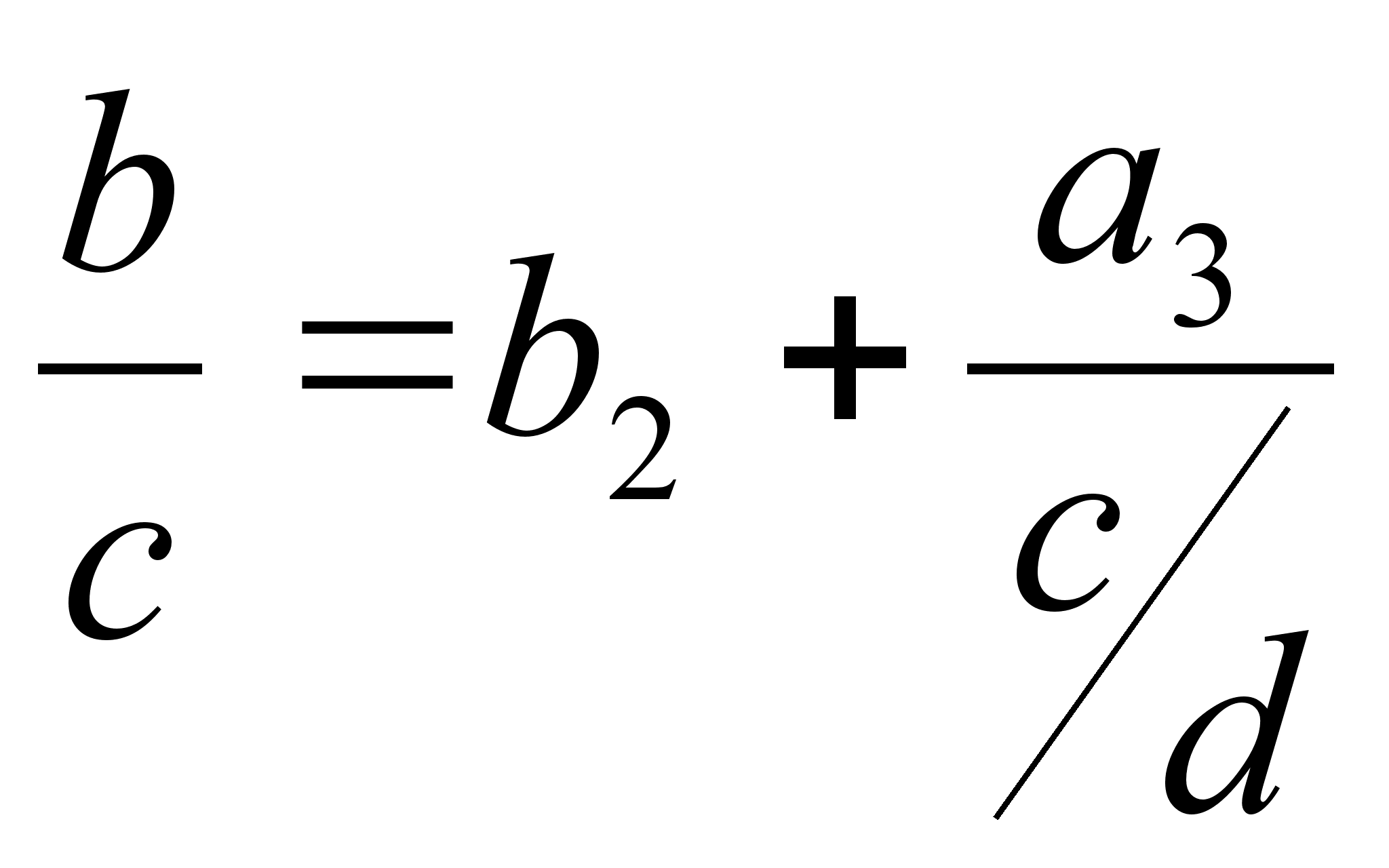 ,
, 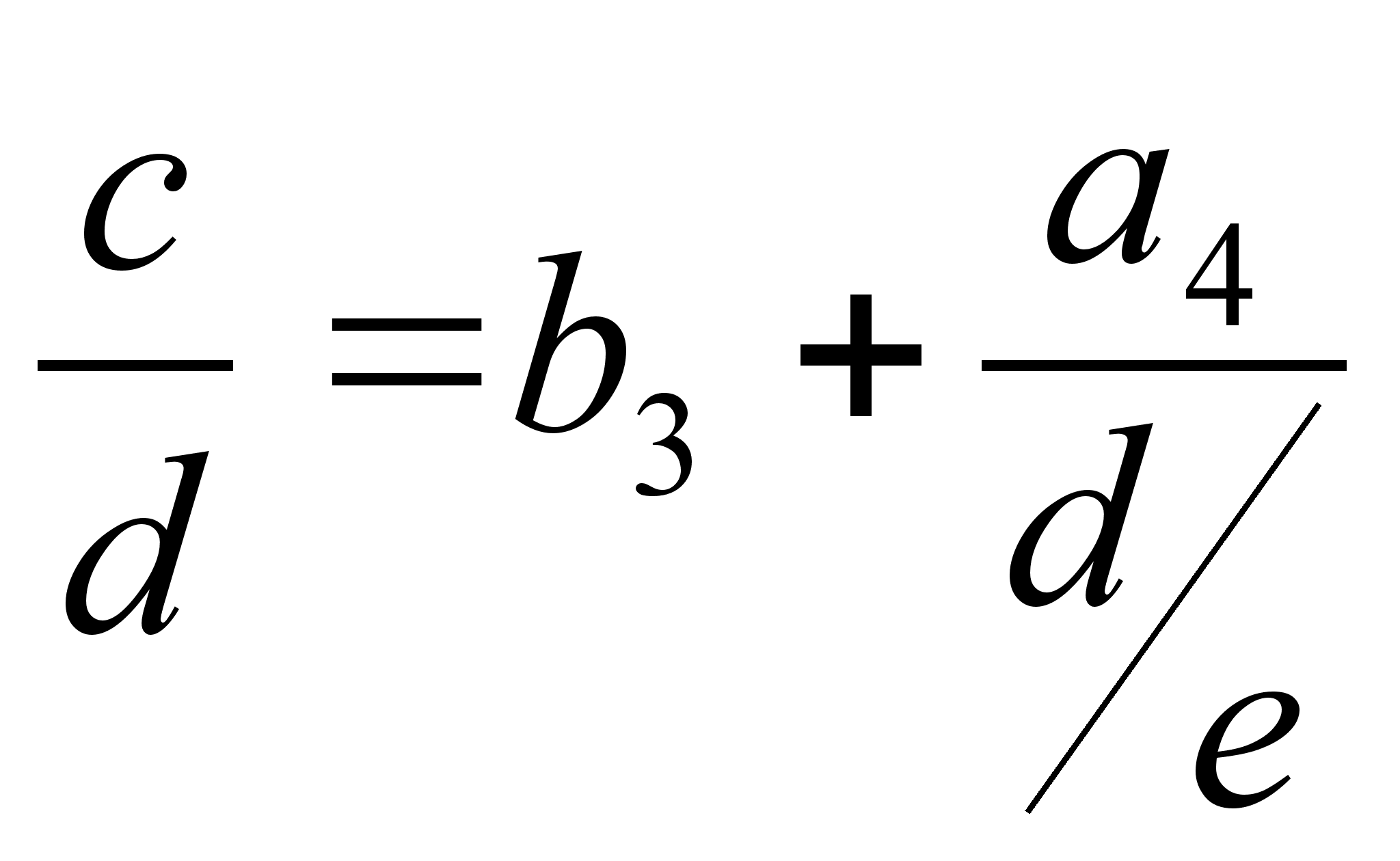 ,
…, так
что, подставляя
по цепочке,
получаем
,
…, так
что, подставляя
по цепочке,
получаем 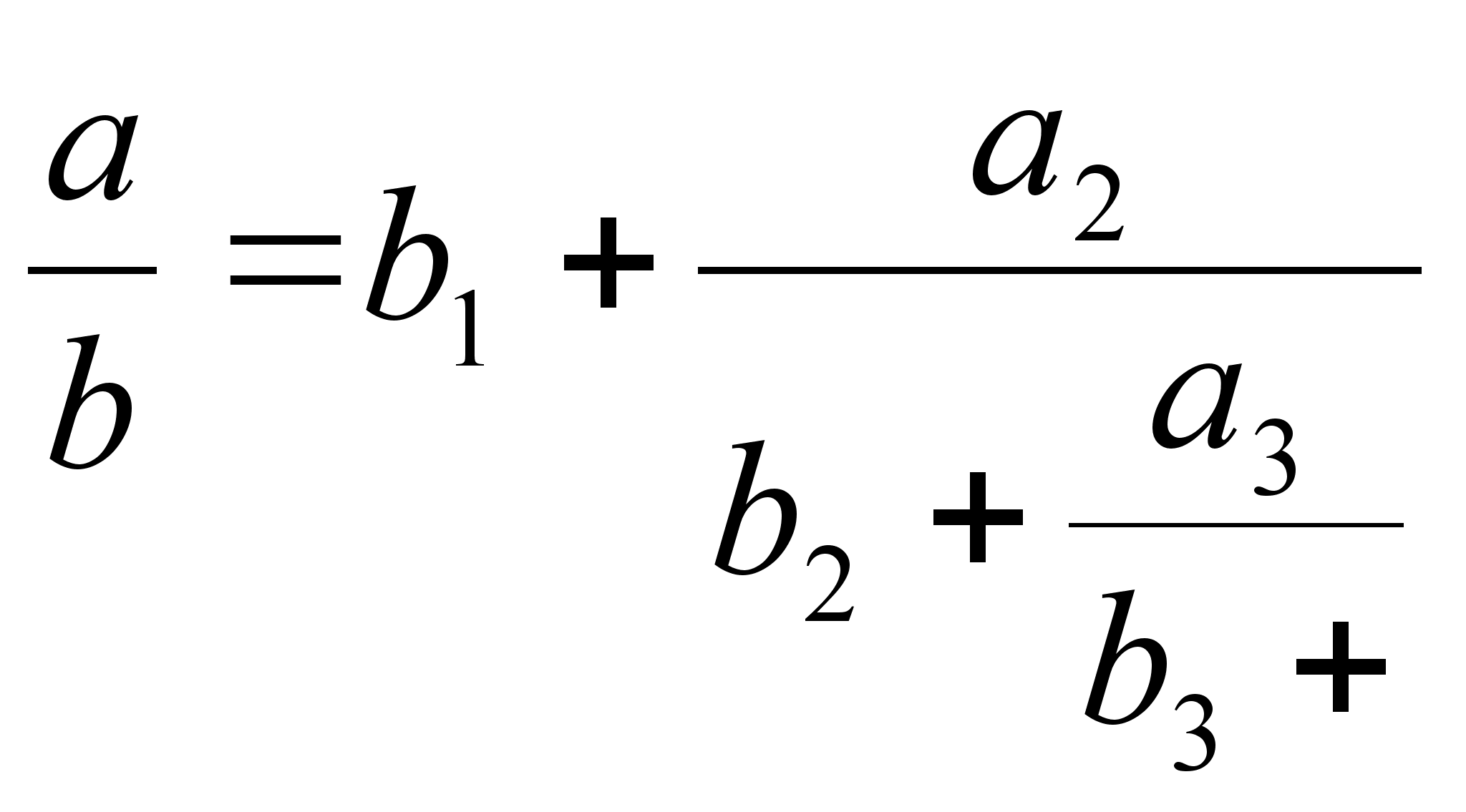 .
.
![]()
k-я
подходящая
дробь
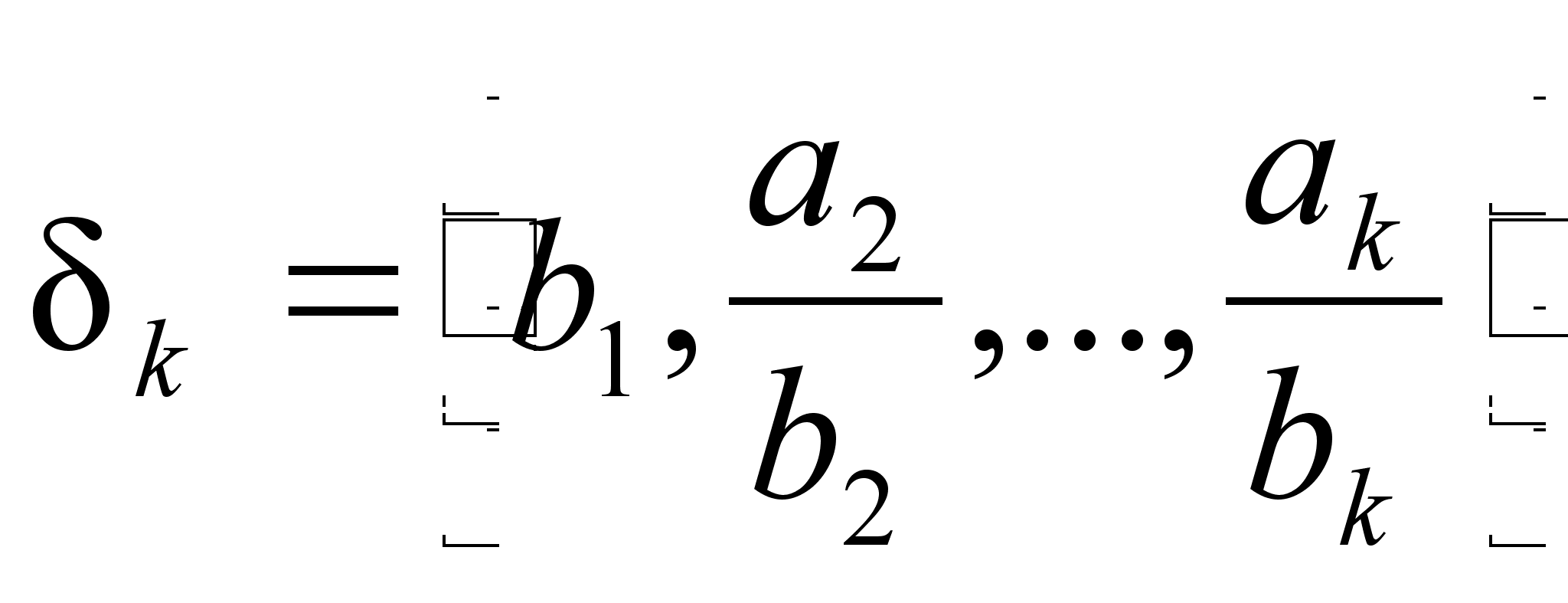 определяется
для
определяется
для
![]() по формуле
по формуле
![]() при условии,
что
при условии,
что ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пользуясь
ею, найдем, например,
подходящие
дроби для разложения
![]() .
Имеем
.
Имеем ![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Заметим, что
получаемые
в процессе
рекуррентного
вычисления
подходящие
дроби могут
быть сократимыми,
но сокращать
их можно лишь
при определенных
условиях.
.
Заметим, что
получаемые
в процессе
рекуррентного
вычисления
подходящие
дроби могут
быть сократимыми,
но сокращать
их можно лишь
при определенных
условиях.
Свойства подходящих дробей цепных дробей общего вида с положительными элементами и правильных цепных дробей вполне аналогичны.
Бесконечная
цепная дробь
(1) называется
сходящейся,
если существует
конечный предел
![]() ;
в таком случае
;
в таком случае ![]() принимается
за значение
этой дроби. Не
всегда общие
бесконечные
цепные дроби
являются сходящимися,
даже тогда,
когда они имеют
лишь положительные
элементы.
принимается
за значение
этой дроби. Не
всегда общие
бесконечные
цепные дроби
являются сходящимися,
даже тогда,
когда они имеют
лишь положительные
элементы.
Существует ряд признаков сходимости цепных дробей:
Пусть дана непрерывная дробь вида
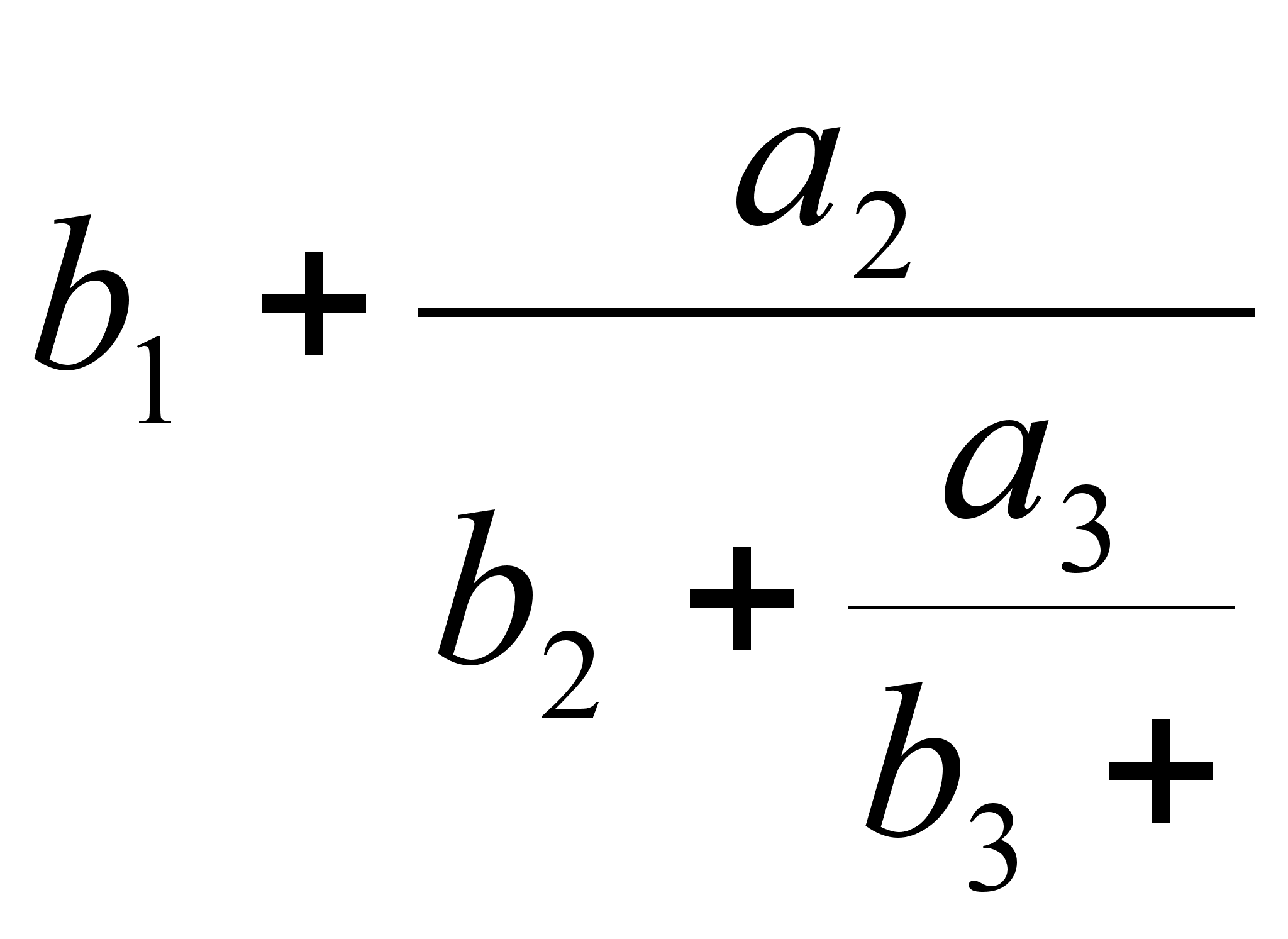 ,
где
,
где ![]() ,
, ![]()
![]()
Пусть ![]() , все члены последовательностей
, все члены последовательностей ![]() ,
, ![]() действительные числа и
действительные числа и ![]() для всех
для всех ![]() , начиная с некоторого. Если для таких k выполняется неравенство
, начиная с некоторого. Если для таких k выполняется неравенство ![]() , то цепная дробь сходится.
, то цепная дробь сходится.
Пусть ![]() и все члены последовательности
и все члены последовательности ![]() , начиная с k=2 положительны. Тогда цепная дробь сходится тогда и только тогда, когда ряд
, начиная с k=2 положительны. Тогда цепная дробь сходится тогда и только тогда, когда ряд ![]() расходится (теорема Зейделя).
расходится (теорема Зейделя).
Интересной особенностью цепных дробей общего вида является то, что даже рациональные числа могут ими разлагаться в бесконечные цепные дроби. Например, имеется разложение
![]()
![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
…
,
…
0,3; 0,42; 0,45; 0,467; …
Примечательно то, что квадратические иррациональности разлагаются и в непериодические цепные дроби общего вида.
Например, имеется разложение
![]()
![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
…
,
…
1; 1,5; 1,38; 1,44; 1,40; …
Но самое
интересное
и важное это
то, что в то время
как до настоящего
времени неизвестно
разложение
в правильную
цепную дробь
ни одной алгебраической
иррациональности
степени выше
второй (другими
словами, неизвестны
общие свойства
неполных частных
таких разложений,
разложения
сами по себе
со сколь угодной
точностью можно
практически
найти), при помощи
общих цепных
дробей такие
разложения
находятся
довольно легко.
Отметим, например,
некоторые
разложения
и соответствующие
подходящие
дроби для ![]() :
:
![]()
![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
…
,
…
1,33; 1,22; 1,284.
![]()
![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
…
,
…
1,17; 1,25; 1,258; 1,2596; …
Приведем еще несколько примеров разложений других иррациональностей в цепные дроби общего вида:
![]()
![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
…
,
…
Эта цепная
дробь для
![]() была найдена
еще более 300 лет
назад английским
математиком
Брункером.
была найдена
еще более 300 лет
назад английским
математиком
Брункером.
![]()
![]() =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
В 1776 году
И. Ламберт нашел
разложение
tg
x в
цепную дробь:
tg
x=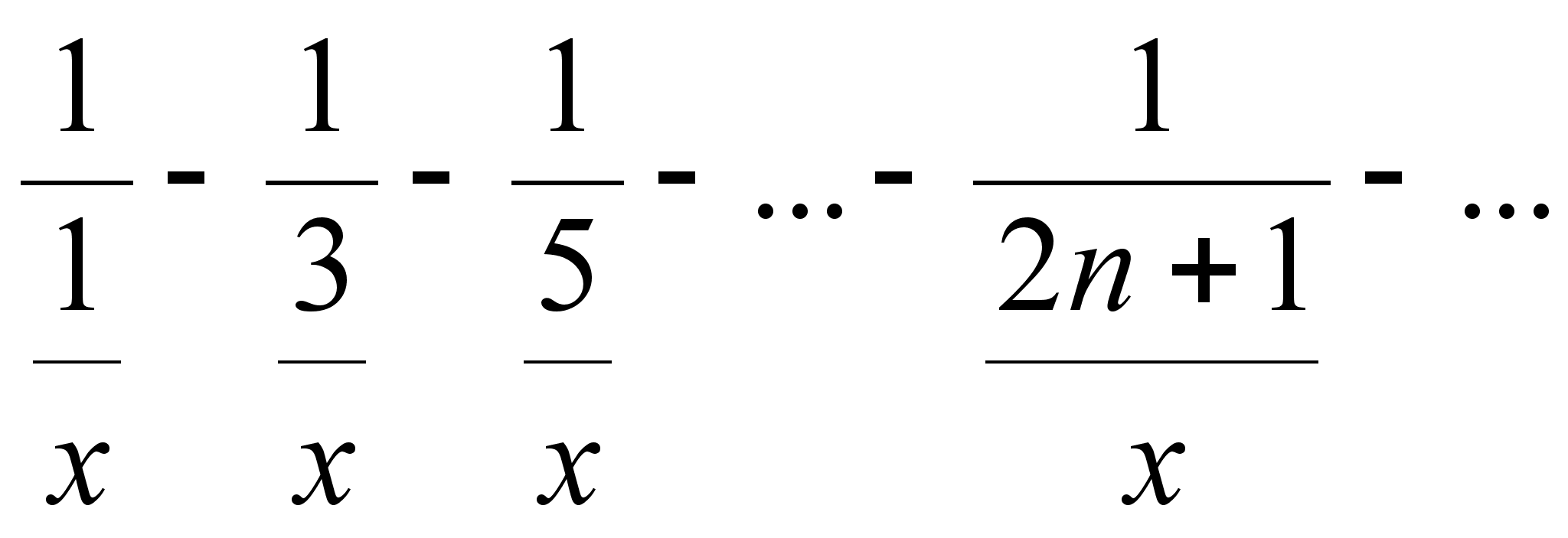
А. Лежандр
в предположении,
что эта цепная
дробь сходится,
показал, что
ее значение
для рациональных
значений
x
иррационально.
Принято считать,
что тем самым
была доказана
иррациональность
числа ![]() .
.
Л. Эйлер
нашел, что: ![]() =(1;
6, 10, 14, …).
Также Эйлер
нашел разложение
в цепную дробь
числа e.
e=(2;
1, 2, 1, 1, 4, 1, 1, 6, …),
то есть элементы
=(1;
6, 10, 14, …).
Также Эйлер
нашел разложение
в цепную дробь
числа e.
e=(2;
1, 2, 1, 1, 4, 1, 1, 6, …),
то есть элементы
![]() разложения
e
в цепную дробь
имеют вид:
разложения
e
в цепную дробь
имеют вид:
![]() ,
, ![]() ,
, ![]()
Швейцарский
математик
Иоганн Генрих
Ламберт (1728-1777) нашел
разложение
числа
![]() в виде цепной
дроби.
в виде цепной
дроби.
Первые
25 неполные частные
разложения
числа
![]() в правильную
цепную дробь
есть числа:
в правильную
цепную дробь
есть числа:
3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1.
Решение задач
Записать в виде конечной цепной дроби
a) ![]() ;
b)
;
b) ![]() ;
c)
;
c) ![]() 2,98976;
d)
2,98976;
d) ![]()
Решение:
![]() =(0, 2, 15);
=(0, 2, 15);
![]() =(3, 7, 15, 1, 292);
=(3, 7, 15, 1, 292);
2,98976=![]() =(2, 1, 96, 1, 1, 1, 10);
=(2, 1, 96, 1, 1, 1, 10);
![]() =–(2, 1, 30, 2)=(-2, 1, 30, 2)
=–(2, 1, 30, 2)=(-2, 1, 30, 2)
Разложить простую дробь в цепную дробь и найти ее подходящие дроби.
a) ![]() ;
b)
;
b) ![]() ;
c)
;
c) ![]() ;
d)
;
d) ![]()
Решение:
a)
![]() =(3,
2, 1, 24);
=(3,
2, 1, 24);
Находим подходящие дроби:
| 3 | 2 | 1 | 24 | ||
|
| 1 | 3 | 7 | 10 | 247 |
|
| 0 | 1 | 2 | 3 | 74 |
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]()
b)
![]() =(3,
3, 33);
=(3,
3, 33);
| 3 | 3 | 33 | ||
|
| 1 | 3 | 10 | 333 |
|
| 0 | 1 | 3 | 100 |
![]() =
=![]() ;
; ![]() =
=![]()
c)
![]() =
= =(3,
7, 15, 1, 292);
=(3,
7, 15, 1, 292);
| 3 | 7 | 15 | 1 | 292 | ||
|
| 1 | 3 | 22 | 333 | 355 | 103993 |
|
| 0 | 1 | 7 | 106 | 113 | 33102 |
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ;
;
d)
![]() =(0,
2, 2, 3);
=(0,
2, 2, 3);
| 0 | 2 | 2 | 3 | ||
|
| 1 | 0 | 1 | 2 | 7 |
|
| 0 | 1 | 2 | 5 | 17 |
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() .
.
Похожие работы
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
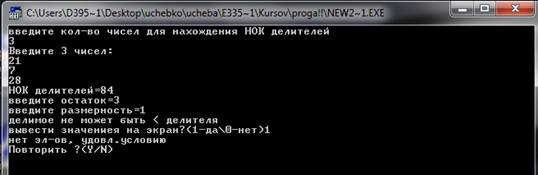
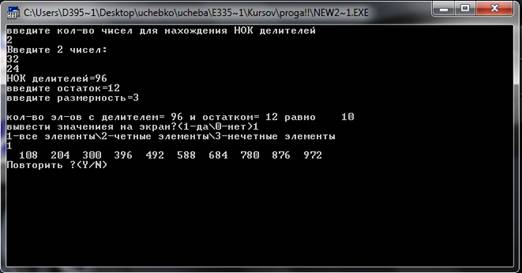
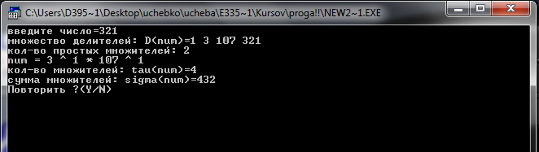
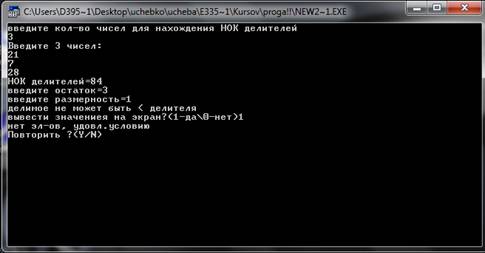
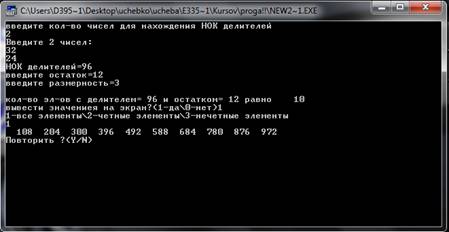
... так делаем, пока не закончатся элементы цепной дроби. Пример. Цепная дробь: [2,3,4,5] Рациональная дробь: 157/68 Тесты. 1.Некорректные данные 2.Корректные данные Заключение Разработана программа CalcKurs, выполняющая следующие функции: 1.формирование заданного подмножества натурального ряда с помощью общего делителя; 2.факторизация числа с опциями; 3.нахождение НОД и НОК ...
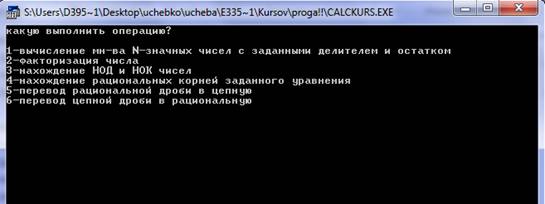
... ; q: char; begin writeln ('Дискретная математика'); writeln ('Курсовая работа, группа 03-119, каф308'); writeln ('выполнил: Тузов И.И. '); writeln ('руководитель: Гридин А.Н. '); writeln; writeln ('Калькулятор с функциями, описанными ниже'); writeln; Writeln ('Нажмите Enter'); readln; clrscr; repeat writeln ('Какую выполнить операцию? '); writeln; writeln ('1-вычисление мн-ва N- ...
... что если уравнение (25) имеет хотя бы одно решение, то оно имеет их бесчисленное множество. Нельзя, конечно, утверждать, что формулами (31) даются все решения уравнения (25). В теории алгебраических чисел доказывается, что все решения уравнения (25) в целых числах можно получить, взяв некоторое конечное и определенное зависящее от и число решений этого уравнения и размножив их с помощью формул ...
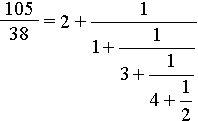
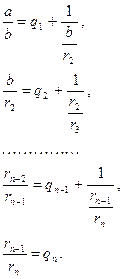
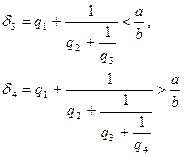
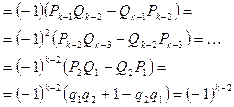
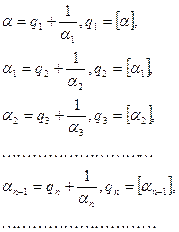
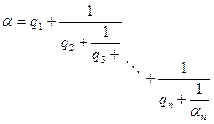
0 комментариев