Навигация
Решение уравнений в целых числах
24303
знака
27
таблиц
7
изображений
СОДЕРЖАНИЕ:
| Уравнения с одним неизвестным |
|
| Уравнения первой степени с двумя неизвестными |
|
| Примеры уравнений второй степени с тремя неизвестными |
|
| Общий случай уравнения второй степени с двумя неизвестными |
|
| Р А З Р А Б О Т К А П Р О Г Р А М М | |
| Программа №1 (уравнения с одним неизвестным) |
|
|
|
|
|
|
|
|
|
|
|
|
|
ВВЕДЕНИЕ
Мой курсовой проект посвящен одному из наиболее интересных разделов теории чисел - решению уравнений в целых числах.
Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших проблем теории чисел.
Проблема решения уравнений в целых числах решена до конца только для уравнений второй степени с двумя неизвестными. Отметим, что для уравнений любой степени с одним неизвестным она не представляет сколько-нибудь существенного интереса, так как эта задача может быть решена с помощью конечного числа проб. Для уравнений выше второй степени с двумя или более неизвестными весьма трудна не только задача нахождения всех решений в целых числах, но даже и более простая задача установления существования конечного или бесконечного множества таких решений.
В своем проекте я постаралась изложить некоторые основные результаты, полученные в теории; решения уравнений в целых числах. Теоремы, формулируемые в нем, снабжены доказательствами в тех случаях, когда эти доказательства достаточно просты.
1. УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение первой степени с одним неизвестным
|
| (1) |
Пусть коэффициенты уравнения 
и 
- целые числа. Ясно, что решение этого уравнения
|
|
будет целым числом только в том случае, когда нацело делится на . Таким образом, уравнение (1) не всегда разрешимо в целых числах; так, например, из двух уравнений 
и 
первое имеет целое решение 
, а второе в целых числах неразрешимо.
С тем же обстоятельством мы встречаемся и в случае уравнений, степень которых выше первой: квадратное уравнение 
имеет целые решения 
, 
; уравнение в целых числах неразрешимо, так как его корни 
,иррациональны.
Вопрос о нахождении целых корней уравнения n-ой степени с целыми коэффициентами
|
| (2) |
решается легко. Действительно, пусть 
- целый корень этого уравнения. Тогда
|
|
,
.Из последнего равенства видно, что делится 
без остатка; следовательно, каждый целый корень уравнения (2) является делителем свободного члена уравнения. Для нахождения целых решений уравнения надо выбрать те из делителей , которые при подстановке в уравнение обращают его в тождество. Так, например, из чисел 1, -1, 2 и -2, представляющих собой все делители свободного члена уравнения
|
|
,только -1 является корнем. Следовательно это уравнение, имеет единственный целый корень 
. Тем же методом легко показать, что уравнение
|
|
в целых числах неразрешимо.
Значительно больший интерес представляет решение в целых числах уравнении с многими неизвестными.
Похожие работы
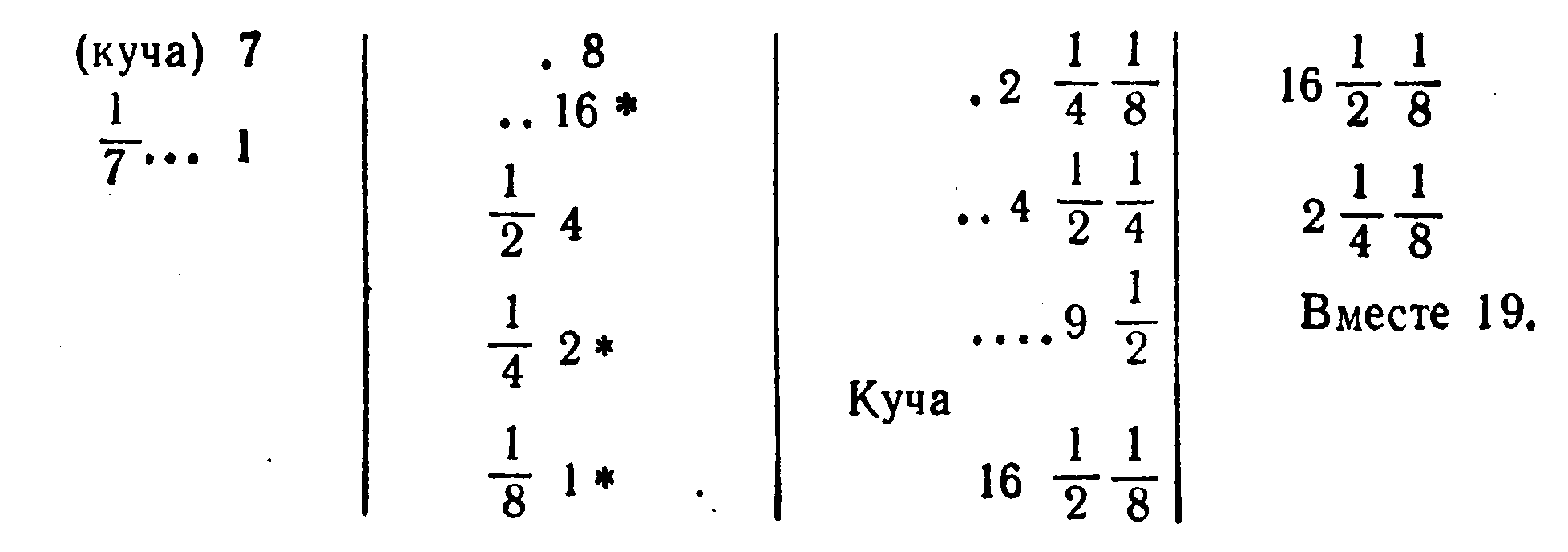
... в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. . Как составлял и решал Диофант квадратные уравнения , В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится ...
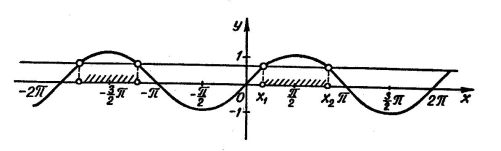
дробно рассмотрено преобразование групп общих решений тригонометрических уравнений. В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе. В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и ...
... ; , т.е. . ; Получили общее решение: , где . Способ 2. Рассмотрим еще один способ нахождения решения ЛДУ с двумя неизвестными, а для этого рассмотрим уравнение вида . Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную , через неизвестную приходим к . Так как x должен быть целым числом, то, где - произвольное целое число. Значит. ...
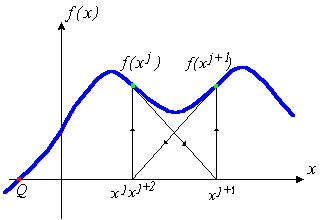
... если точка начального приближения далека от точки решения, то метод Ньютона - Рафсона может не сходиться совсем. Геометрическая интерпретация не сходящегося метода Ньютона - Рафсона приведена на рис. 1б. Алгоритм Назначение: поиск решения уравнения (1) Вход: Начальное приближение x0 Точность (число итераций I) Выход: xI - решение уравнения (1) Инициализация: calculate f’(x0) Шаги ...
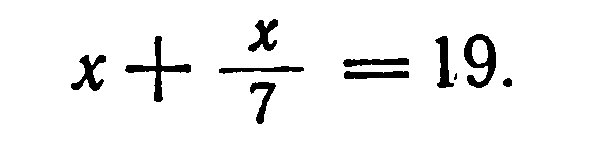
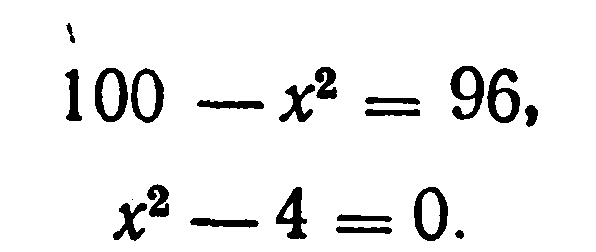
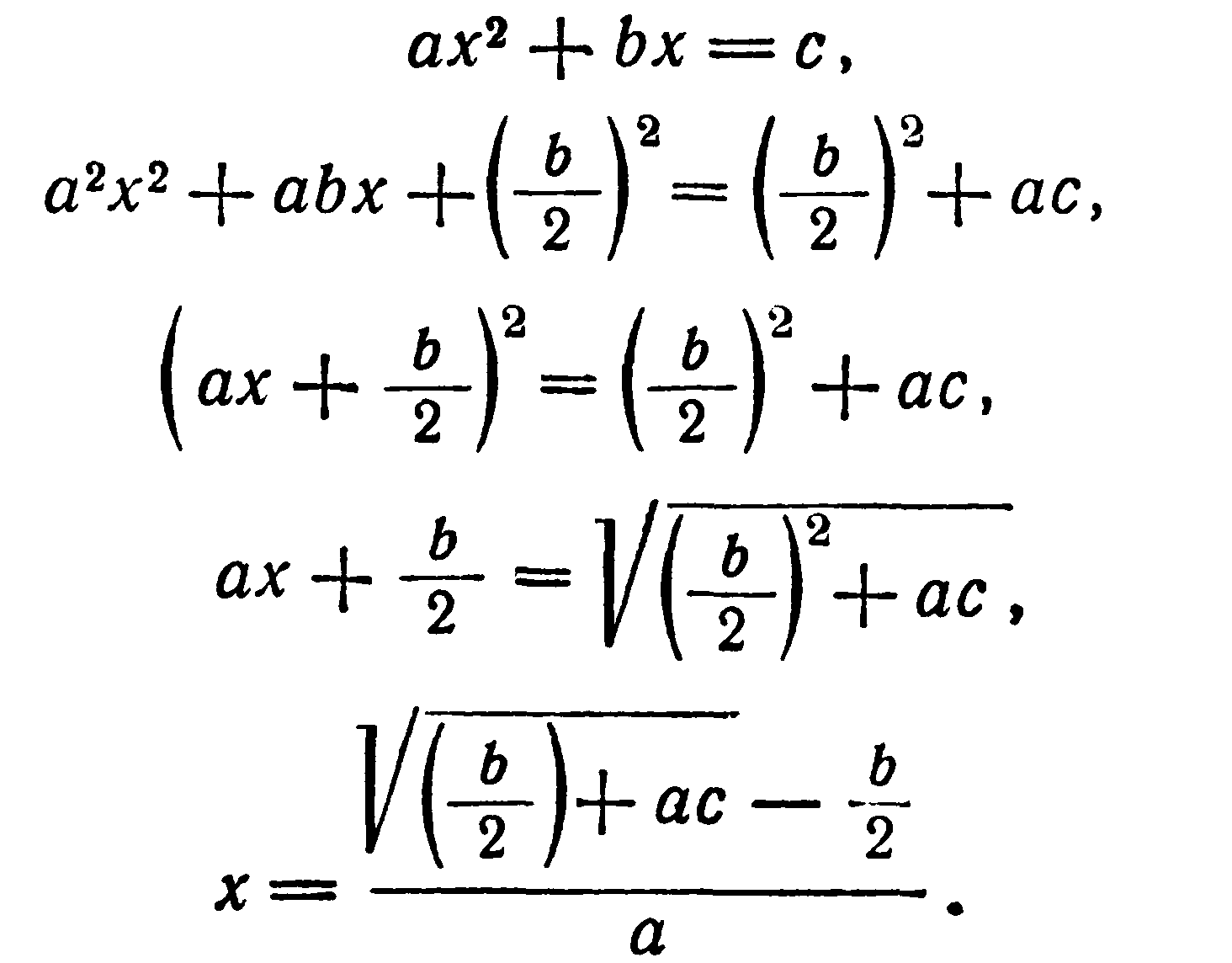
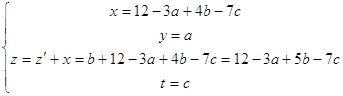
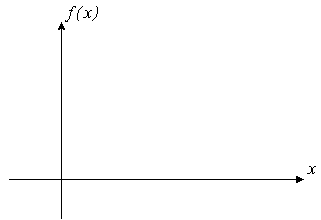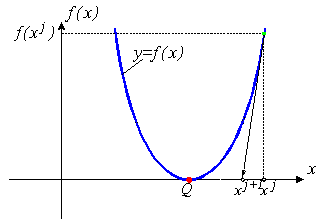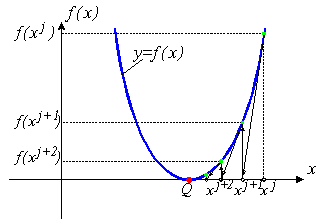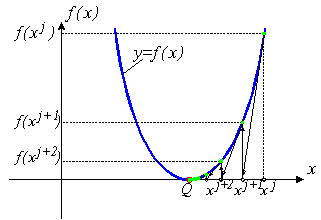
0 комментариев