Навигация
ОПРЕДЕЛЕНИЕ ПЕРИОДА КВАНТОВАНИЯ ЦИФРОВОГО РЕГУЛЯТОРА И ПЕРЕСЧЕТ ЕГО ВАРАМЕТРОВ
3 ОПРЕДЕЛЕНИЕ ПЕРИОДА КВАНТОВАНИЯ ЦИФРОВОГО РЕГУЛЯТОРА И ПЕРЕСЧЕТ ЕГО ВАРАМЕТРОВ
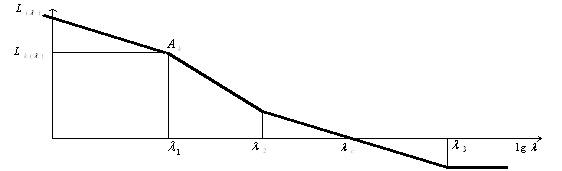
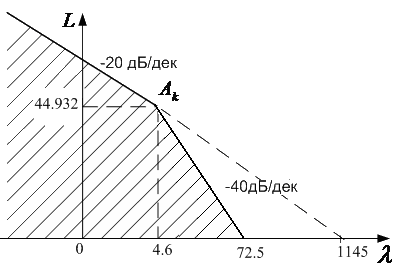
Необходимо выяснить соответствие коэффициентов неопределенногои цифрового регуляторов. Для выбора периода измерений цифрового регулятора строим амплетудно – частотную характеристику замкнутой системы и определяем частоту среза, при которой значение амплетуды на выходе не превышает три проценты от амплитуды при нулевом значении частоты.
Для этого возьмем передаточные функции замкнутой системы (для все типов регуляторов), которые были найдены во втором задании курсовой работы.
Передаточная функция замкнутой системы с П – регулятором:
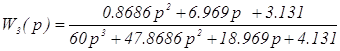 , (3.1)
, (3.1)
Передаточная функция замкнутой системы с ПИ– регулятором:
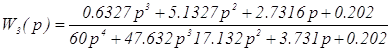 , (3.2)
, (3.2)
Передаточная функция замкнутой системы с ПИД – регулятором:
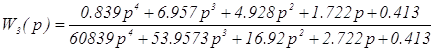 , (3.3)
, (3.3)
Выражение амплетудно – частотной характеристики для системы с П – регулятором будет иметь следующий вид:
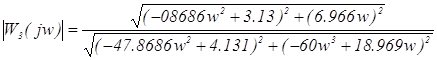 . (3.4)
. (3.4)
Выражение амплетудно – частотной характеристики для системы с ПИ – регулятором будет иметь следующий вид:
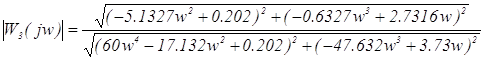 . (3.5)
. (3.5)
Выражение амплетудно – частотной характеристики для системы с ПИД – регулятором будет иметь следующий вид:
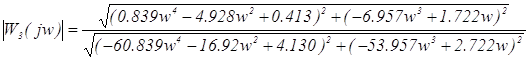 . (3.6)
. (3.6)
Така как частота среза равна трем процентам от нулевого значения, то необходимо решить уравнение следующего вида:
![]() . (3.7)
. (3.7)
При решении уравнений было получено:
-частота среза для системы имеющей в стоем составе П – регулятор wс = 2.25;
-частота среза для системы имеющей в стоем составе ПИ – регулятор wс = 1.6738;
-частота среза для системы имеющей в стоем составе ПИД – регулятор wс = 3.8194.
Частоту измерений принимают как:
![]() , (3.8)
, (3.8)
где wc = 3.8194 (наибольшее значение), при котором период квантования равен T0 = 0.411.
Так как полученное значение меньше заданного, то произведем пересчет параметров.
В общем виде дискрктную передаточную функцию искоиого элемента можно записать следующим образом:
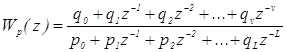 . (3.9)
. (3.9)
В нашем случае выражение (3.9) примет вид:
![]() , (3.10)
, (3.10)
 где
где 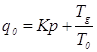 ;
;
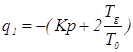 ;
;
![]() .
.
C учетом этих выражений необходимо пересчитать параметры непрерывных регуляторов в параметры цифровых.
Запишем передаточные функции непрерывных регуляторов:
- П – регулятор
Wp(p) = 1.01; (3.11)
- ПИ – регулятор
![]() ; (3.12)
; (3.12)
- ПИД – регулятор
![]() . (3.13)
. (3.13)
После вычисления коэффициентов q0, q1 и q2 дискрктные передаточные функции будут иметь вид:
- П – регулятор
![]() ; (3.14)
; (3.14)
- ПИ – регулятор
![]() ; (3.15)
; (3.15)
- ПИД – регулятор
![]() .
(3.17)
.
(3.17)
4 АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО УТРАВЛЕНИЯ ПО КРИТЕРИЮ ДЖУРИ И ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦИФРОВЫХ СИСТЕМАХ
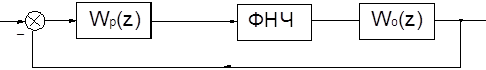 |
При анализе цифровых систем управления их представляют в виде трех элементов: цифрового фильтра (регулятора), фиксатора и приведенной непрерывной части.
где y – дискретное значение регулируемой величины;
f – заданное значение регулируемой величины;
e – ошибка управления;
u – управляющее воздействие.
Рисунок 4.1 Структурная схема цифровой системы автоматического управления
Так как в системе имеет мести фиксатор нулевого порядка с передаточной функцией вида:
![]() , (4.1)
, (4.1)
то с учетом того, что z = e –pT , эту функцию можно записать в следующем далее виде:
![]() .
(4.2)
.
(4.2)
Сомножитель 1/р относят к линейной части, поэтому передаточная функция приведенной непрерывной части может быть записана в следующем виде:
![]() .
(4.3)
.
(4.3)
![]()
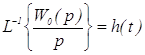 ,
,
переходная фнукция ленейной части системы, то z – передаточную функцию линейной части находим по следующему выражению:
![]() .
(4.4)
.
(4.4)
Найдем выражение для передаточной функции линейной части:
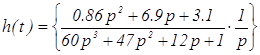 .
(4.5)
.
(4.5)
Для вычисления h(t) воспользуемся методом неопределенных коэффициентов. Необходимо определить полюса. Для этого необходимо найти корни следйющего уравнения:
(![]() )*р = 0.
)*р = 0.
Решив данное уравнение мы получили , что его корни следующего вида:
p1 = 0;
p2 = - 0,2;
p3 = - 0,33;
p4= -0,25.
Переходная функция линейной части имеет следующий вид:
h(t) = -21,93e-0.2t –4.03e-0.33t +22.86e-0.25t +3.1 . (4.6)
С учетом формулы (4.4) получаем
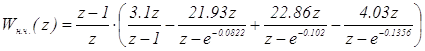 .
.
После раскрытия скобок и приведения подобных мы получаем равенство в следующем виде:
![]() . (4.7)
. (4.7)
Результирующая передаточная функция разомкнутой системы может быть определена как произведение передаточной функции приведенной непрерывной чати и передаточной функции цифрового фильтра:
![]() . (4.8)
. (4.8)
Дискретная передаточная функция замкнутой системы:
![]() . (4.9)
. (4.9)
Определим значение W3(z) для каждой из систем:
- система с П – регулятором. Wр(z) = 1.01, Wн.ч.(z) – определеня по формуле (4.7), тогда:
![]() ; (4.10)
; (4.10)
- система с ПИ – регулятором.
![]() ;
;
Wн.ч.(z) – определена по формуле (4.7), тогда:
![]() ; (4.11)
; (4.11)
- система с ПИД – регулятором.
![]() ,
,
Wн.ч.(z) – определена по формуле (4.7), тогда:
![]() .
(4.12)
.
(4.12)
После того , как получим выражение дискрктных передаточных функций для всех систем, проанализируем устойчивость этих систем по критерию Джури.
Критерий устойчивости заключается в следующем.
Пусть задан А(z) – характкристический полином:
A(z) = a0zn + a1n-1 + … + an, a0 > 0.
Введем понятие обратного полинома, получаемого перестановкой коэффициентов исходного в обратном порядке:
A(z) = anzn + an-1n-1 + … + a0.
Разделим A(z) на обратной ему. В итоге получаем частное от деления число q0 и остаток А1(z) – полином n-1 степени.
Домножим полученый результат на z-1 получаем:
A1(z) = (a0-anq0)zn-1 + … + (an-1-a1q0).
Затем делим остаток A1(z) на обратный ему A10(z) и определяем новое q1 и A2(z)
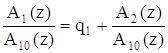 и т.д.
и т.д.
Выполняя деление полиномов Ai(z) на обратные ему Ai0(z), получаем последовательность чисел qi = {q0, q1, q2,…,qn-2}.
Необходимым и достаточным условием устойчивости цифровой системы является неравенства:
А(1)=(a0+ a1+ a2+…+an)>0;
(-1)nА(-1)=(a0(-1)n + a1(-1)n-1 +…+an)>0;
|qi|<1, i=0,1,2,…,n-2.
Используя выше изложенное, определим устойчивость наших систем.
Система с П-регулятором.
Характеристический полином имеет следующий вид:
А(1)= 1 - 2.7544 + 2.5359 - 0.7817=0.003039>0 .
(-1)3A(-1)= -(1 - 2.7544 + 2.5359 - 0.7817) >0.
А(z) = z3-2.7544z2+2.5359z - 0.7817
Обратный полином![]() .
.
Разделим A(z) на A0(z).
|
|
|
| -( | -0.7817=q0, |q0|<1 |
0,3852z-0,7686z2+0,3888z3
Домножим полученный результат на z-1, тогда:
A1(z)= 0,3852-0,7686z+0,3888z2,
A10(z)= 0,3888-0,7686z+0,3852z2.
Разделим A1(z) на A10(z).
| 0,3852-0,7686z+0,3888z2 | 0,3888-0,7686z+0,3852z2 |
| -(0,3852-0,7614z+0,3816z2) | 0,99065=q1, |q1|<1 |
-0.00718z+0.00723z2
Домножим полученный результат на z-1, тогда:
A2(z)= 0.007238z-0.007187.
В результате расчетов получили, что q0, q1, q2 по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.
Система с ПИ-регулятором.
Характеристический полином имеет вид:
Степень полинома n=4. Множество qi = {q0, q1, q2}.
А(1)= ![]() >0.
>0.
(-1)4A(-1)= ![]() >0.
>0.
![]() .
.
Обратный полином:
![]() .
.
Разделим A(z) на A0(z).
| 0.78-3.326z+5.3001z2-3.756z3+ z4 | 1-3.7556z+5.3001z2-3.32z3+0.7834z4 |
| -(0.78-2.943z+4.152z2-2.606z3+0.61z4) | 0,783447=q0, |q0|<1 |
-0,383z+1.147z2-1.1506z3+0,3861 z4
Домножим полученный результат на z-1, тогда:
A1(z)= -0,383+1.147z-1.1506z2 +0,3861 z3,
A10(z)= -0,361+1.1506z-1.147z2 +0,383 z3.
Разделим A1(z) на A10(z).
| -0,383+1.147z-1.1506z2 +0,3861 z3 | -0,361+1.1506z-1.147z2 +0,383 z3 |
| -(-0,383+1.141z-1.138z2 +0,3801 z3) | -0,992116=q1, |q1|<1 |
0,006046z-0,01207z2+0,00605z3
Домножим полученный результат на z-1, тогда:
A2(z)= 0,006046z-0,01207z2+0,00605z3,
A20(z)= 0,00605-0,005474z2-0,006046z3.
Разделим A2(z) на A20(z).
| 0,006046z-0,01207z2+0,00605z3 | 0,00605-0,005474z2-0,006046z3 |
| -(0,006046z-0,01207z2+0,00603z3) | 0,99774=q2, |q2|<1 |
-0,000027278z+0,000027353z2
Домножим полученный результат на z-1, тогда:
A3(z) = -0,000027278z+0,000027353z2
В результате расчетов получили, что q0, q1, q2 по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.
Система с ПИД-регулятором.
Характеристический полином имеет вид:
Степень полинома n=5. Множество qi = {q0, q1, q2, q3}.
А(1)=![]() >0.
>0.
(-1)5A(-1)=![]() >0.
>0.
![]() ,
,
Обратный полином:
![]() .
.
Разделим A(z) на A0(z).
|
|
|
|
| 0,01589163=q0, |q0|<1 |
0,7347z-3,1644z2+5,102835z3-3,6802818z4+0,999747z5
Домножим полученный результат на z-1, тогда:
A1(z)= 0,7347-3,1644z+5,102835z2-3,6802818z3+0,999747z4,
A10(z)= 0.99974 -3,680218z+5,1028z2-3,1644z3+0,7347z4.
Разделим A1(z) на A10(z).
| 0,7347-3,1644z+5,102835z2-3,6802818z3+0,999747z4 | 0,7347-3,1644z+5,102835z2-3,6802818z3+0,999747z4 |
| -(0,7347-2.704z+3.750z2-2.3256z3+0.53999z4) | 0,734938361=q1, |q1|<1 |
-0,4596z+1,3255z2-1,3545z3+0,4597z4
Домножим полученный результат на z-1, тогда:
A2(z)= -0,4596+1,3255z-1,3545z2+0,4597z3,
A20(z)= -0,4597+1,3545z-1,3255z2+0,4596z3.
Разделим A2(z) на A20(z).
| -0,4596+1,3255z-1,3545z2+0,4597z3 | -0,4597+1,3545z-1,3255z2+0,4596z3 |
| -0,4596-1,3244z+1,3525z2+0,4595z3 | -0,99986442=q2, |q2|<1 |
-0,0288981z-0,02926z2+0,91927z3
Домножим полученный результат на z-1, тогда:
A3(z)= -0,0288981-0,02926z+0,91927z2,
A30(z)= 0,91927-0,02926z-0,02889881z2.
Разделим A3(z) на A30(z).
| -0,0288981-0,02926z+0,91927z2 | 0,91927-0,02926z-0,02889881z2 |
| 0,0288981-0,0009198z+0,0.028898z2 | 0,0314359=q2, |q2|<1 |
-0,0305301z+1.028762z2
Домножим полученный результат на z-1, тогда:
A4(z)= -0,0305301+1.028762z.
В результате расчетов получили, что q0, q1, q2 по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.
После того, как определили устойчивость системы по критерию Джури, необходимо построить переходный процессы в замкнутых цифровых системах.
Для построения переходных процессов в замкнутых цифровых системах воспользуемся обратным z-преобразованием.
Eсли функция имеет m-полюсов zk={z1, z2,…, zn} , то:
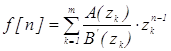 , (4.13)
, (4.13)
где A(zk) – числитель функции W3(z);
B’(zk) – производная знаменателя функции W3(z);
Замкнутая система с П – регулятором.
Передаточная функция для цифровой замкнутой системы с П-регулятором имеет вид:
![]()
Переходная функция замкнутой системы равна:
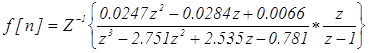 .
.
Для вычисления f[n] найдем полюса функции
![]() .
.
Полюся функции:
z1 = 1;
z2 = 0,8422;
z3 = 0,954 – j0,313;
z4= 0,954 – j0,313.
Производная знаменателя функции:
B’(z) = -11.25z2+10.574z-3.317+4z3.
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для :
где a = z1;
b = z2;
c = z3;
d = z4;

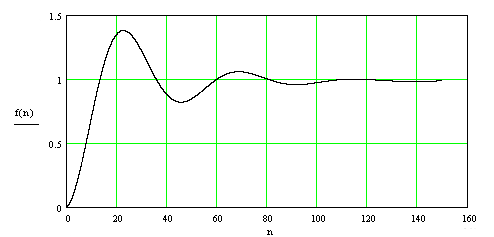
Рисунок 4.2 - Переходный процесс в системе с П – регулятором
Замкнутая система с ПИ – регулятором.
Передаточная функция для цифровой замкнутой системы с ПИ-регулятором имеет вид:
![]() ;.
;.
Переходная функция замкнутой системы равна:
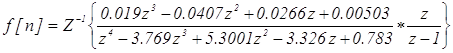 .
.
Для вычисления f[n] найдем полюса функции
![]() .
.
Полюся функции:
z1 = 1;
z2 = 0.847;
z3 = 0.965;
z4 = 0.973 – j0.0113;
z5= 0.973 + j0.0113.
Производная знаменателя функции:
B’(z) = 5z4-19.027z3+27.171 z2-17.253z+4.110
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для f[n]:
где а = z1;
b = z2;
c = z3;
d = z4;
e = z5;

Изобразим переходый процесс на рисунке 4.3
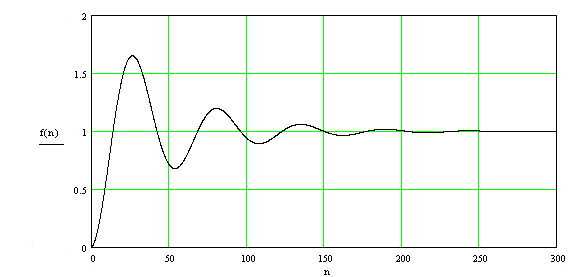
Рисунок 4.3 - Переходный процесс в системе с ПИ – регулятором
Замкнутая система с ПИД – регулятором.
Передаточная функция для цифровой замкнутой системы с ПИД-регулятором имеет вид:
![]() .
.
Переходная функция замкнутой системы равна:
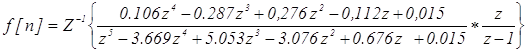 .
.
Для вычисления f[n] найдем полюса функции
![]() .
.
Полюся функции:
z1 = 1;
z2 = -0,021;
z3 = 0,84;
z4 = 0,935-j0,171;
z5= 0,935+j0,171;
z6=0,98.
Производная знаменателя функции:
B’(z) = 6z5-23.347 z4+34.893 z3-24.39 z2+7.505z-0.660
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для f[n]:

где а = z1;
b = z2;
c = z3;
d = z4;
e = z5;
f = z6.
Изобразим переходый процесс на рисунке 4.4
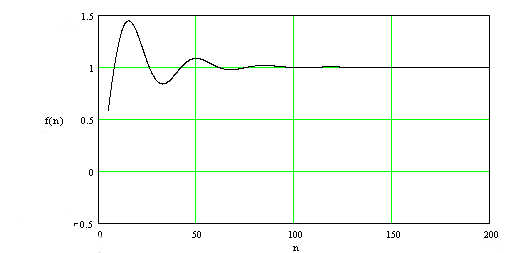
Рисунок 4.4 - Переходный процесс в системе с ПИД – регулятором.
Похожие работы
... принципиальной схемы приведена в Приложении Б Рисунок 3.7 - Принципиальная электрическая схема корректирующего устройства 4. Экономический расчет Затраты на проектирование цифрового регулятора для электропривода с фазовой синхронизацией определяются по формуле: , (1.1) где Сосн, зп - основная заработная плата персонала, руб.; Сдоп, зп - дополнительная заработная плата ...
... вариант To ko T1 T2 kc kв kQ kП ky T3 k3 ν σ c c c c % % 4-9 0.7 6 0.4 0.025 2.5 0.5 200 0.13 0.2 26 0.01 2 2 5 Введение Задача синтеза системы автоматического регулирования заключается в выборе такой её структуры, параметров, характеристик и способов их реализации, ...
... ТРЕБОВАНИЙ И ПОСТАНОВКА ЗАДАЧ ПРОЕКТИРОВАНИЯ 1.1 Расчеты основных параметров электромеханической системы привода В данном курсовом проекте разрабатывается привод подач токарного станка. Для перемещения по координате предусмотрен свой привод. Поэтому разработку производим для одного контура управления. Применение ЦСУ позволяет значительно повысить точность и качество обработки, упростить ...
... правило, выполняется в виде одной «большой» ИМС. Схемотехника является частью микроэлектроники, предметом которой являются методы построения устройств различного назначения на микросхемах широкого применения. Предметом же цифровой схемотехники являются методы построения (проектирования) устройств только на цифровых ИМС. Особенностью цифровой схемотехники является широкое применение для описания ...
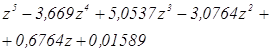
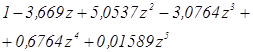
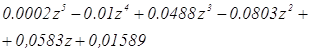


0 комментариев