Навигация
5 Расчет цифрового фильтра
Для расчета цифрового фильтра, переводящего линейную часть из начального в конечное состояние за минимальное число периодов квантования и обеспечивающего ограничение на заданное управляющие воздействие, необходимо вычислить минимально возможный период квантования, но чтобы было удовлетворено условие:
|Um – q0|£0,05, (5.1)
где Um = 1,0.
Вычисление значения q0 следует начать с определения значений коэффициентов числителя Z-передаточной функции приведенной непрерывной части для принятого периода дискретности. Пусть Z-передаточная функция приведенной непрерывной части представима в виде:
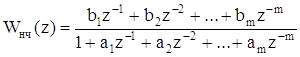 . (5.2)
. (5.2)
Тогда Z-передаточная функция оптимального по быстродействию цифрового фильтра Wф(z) имеет вид:
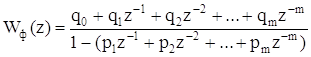 , (5.3)
, (5.3)
где pi = biq0, i = 1,2,…,m;
qi = aiq0, i = 1,2,…,m;
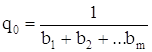 .
.
Воспользуясь формулой (4.7) для Wнч(z) . Находим функции bi , аi и Т0.
Для коэффициентов bi имеем:
![]() ; (5.4)
; (5.4)
![]() ;(5.5)
;(5.5)
![]() . (5.6)
. (5.6)
Для коэффициентов аi имеем:
![]() ; (5.7)
; (5.7)
![]() ; (5.8)
; (5.8)
![]() . (5.9)
. (5.9)
Найдем выражение для q0 :
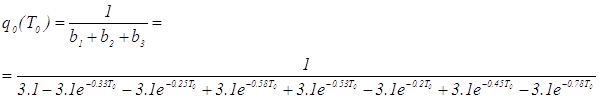
![]() . (5.10)
. (5.10)
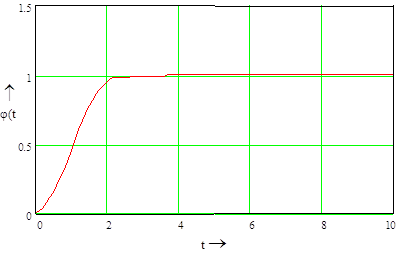
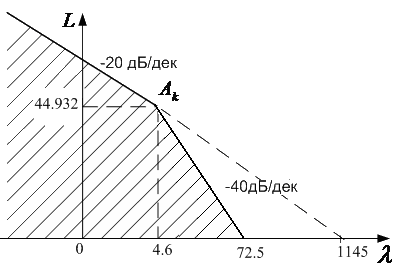
Определим Т0 при котором выполняется условие (5.1), для этого построим график зависимости и изибразим его на следующем рисунке 5.1.

Рисунок 5.1 – График зависимости |Um – q0(Т0)|
При построении графика видим, что Т0 = 4,61 , q0(Т0) = 1,002.
Определим коэффициенты , подставив найденное значение Т0 в выражение (5.4) и (5.5):
b1(Т0) = 0,718;
b2(Т0) = 0,332;
b3(Т0) = -0,052;
a1(Т0) = -0,932;
a2(Т0) = 0,281;
a3(Т0) = -0,027;
Подставляя найденные значения в выражения (5.2) и (5.3) определим передаточные функции приведенной непрерывной части и цифрового фильтра.
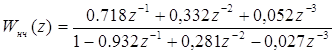 . (5.7)
. (5.7)
![]() . (5.8)
. (5.8)
Находим Z – передаточную функцию для разомкнутой цифровой системы по формуле:
Wp(z) = Wн.ч.(z) * Wф(z). (5.9)
Определим Z – преобразованную функцию замкнутой системы по каналу задание – управляюшее воздействие по формуле:
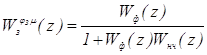 , (5.10)
, (5.10)
Определим Z – преобразованную функцию замкнутой системы по каналу задание – выходной сигнал по формуле:
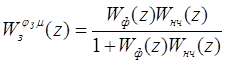 , (5.10)
, (5.10)
Пусть f – функция определяющая зависимость между q0 от Т0, т.е. q0=f(Т0), тогда f –1 – обратная ей функция, т.е. Т0=f –1(q0). Для того, чтобы найти период квантования необходимо минимизировать функцию
Т0=f –1(q0) с учетом условия (5.1).
Так как в явном виде функцию Т0=f –1(q0) вывести сложно, но из графика видно, что она монотонно убывает, следовательно минимум на отрезке q0 Î [3,45; 3,55] будет при q0=3,55.
Расчет Т0 сводится к решению уравнения
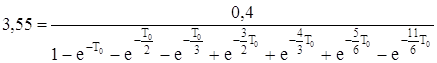 . (5.11)
. (5.11)
Для решения данного уравнения воспользуемся алгоритмом поиска корня уравнения методом дихотомии. После решения уравнения мы получили, что
Т0 =1,25.
Подставляя значение Т0 =1,25 в выражения (5.4)-(5.9) найдем коэффициенты Z-передаточной функций приведенной непрерывной части.
Тогда
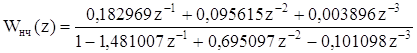 . (5.12)
. (5.12)
При этом q0 =3,540075. Согласно формуле (5.3)
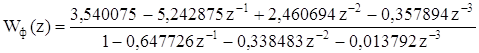 . (5.13)
. (5.13)
Найдем Z-передаточную функцию разомкнутой цифровой системы. Она равна Wр(z)=Wнч(z)*Wф(z) и равна
![]() . (5.14)
. (5.14)
Z-передаточная функция замкнутой цифровой системы по каналу задание – управляющие воздействие равна
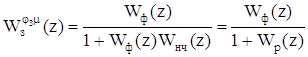 (5.15)
(5.15)
и равна
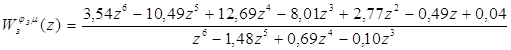 .
.
Z-передаточная функция замкнутой цифровой системы по каналу задание – выходная величина равна
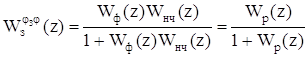 (5.16)
(5.16)
и равна
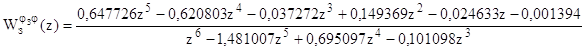 .
.
Вычислим коэффициенты усиления по указанным каналам. По определению коэффициент усиления есть отношение изменения на выходе к изменению на входе в установившемся режиме, т.е.
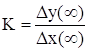 . (5.17)
. (5.17)
Так как
![]() ,
(5.18)
,
(5.18)
то подставляя выражения (5.15) и (5.16) в выражение (5.17) найдем, что j(¥)=1, а m(¥)=0,4. Так как Dx(¥)=1, а j(0-)=0 и m(0-)=0, то коэффициент усиления по каналу задание – выходная величина равен 1, а по каналу задание – управляющие воздействие равен 0,4.
Построим переходную функцию цифрового фильтра. Она равна
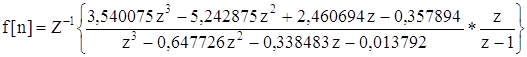 .
.
Для вычисления f[n] найдем полюса функции
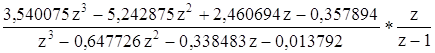 .
.
Находим 2 полюса 1-го порядка и 1 полюс 2-го порядка. Полюса
1-го порядка: z=-0,307 и z=-0,045. Полюс 2-го z=1. Для вычисления переходной функции необходимо вычислить производную следующей функции 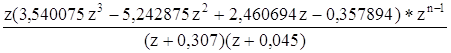 . Производная данного выражения равна
. Производная данного выражения равна
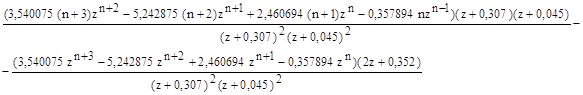 .
.
Тогда передаточная функция примет вид
![]() .
.
Изобразим переходный процесс на графике.
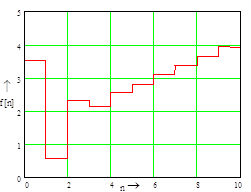
Для построения переходных процессов в замкнутой цифровой системе по каналам задание – выходная величина и задание – управляющие воздействие воспользуемся уравнениями в конечных разностях.
Суть метода заключается в следующем. Пусть передаточная функция цифровой системы
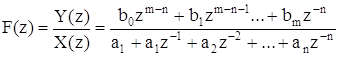 .
.
Этой передаточной функции соответствует уравнение в конечных разностях:
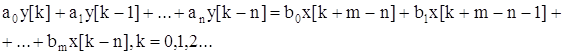 .
.
Значение искомой выходной величины равно
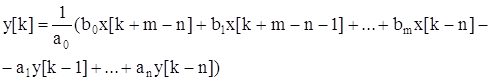 . (5.19)
. (5.19)
Согласно формуле (5.19) получим, что переходная функция замкнутой цифровой системе по:
· каналу задание – выходная величина
y[k]=0,647726×x[k-1] –0,620803×x[k-2] –0,037272×x[k-3] +0,149369×x[k-4] –0,024633×x[k-2] –0,001394×x[k-2] +1,481007×y[k-1] –0,695097×y[k-2]+ +0,101098×y[k-3];
· каналу задание – управляющие воздействие
y[k]=3,540075×x[k] –10,485749×x[k-1] +12,686121×x[k-2] –
–8,004397×x[k-3] +2,770507×x[k-4] –0,497542×x[k-5]+0,036182×x[k-6]+ +1,481007×y[k-1] –0,695097×y[k-2]+ +0,101098×y[k-3].
Данные расчетов были сведены в таблицы с учетом того, что x[k]=1.
Таблица 5.1 – Переходная функция замкнутой цифровой системе по каналу задание – выходная величина
| k | y[k] |
| 0 | 0 |
| 1 | 0,648 |
| 2 | 0,986 |
| 3 | 1 |
| 4 | 1 |
6 Оптимальное управляющие воздействие и реакция на него приведенной непрерывной части
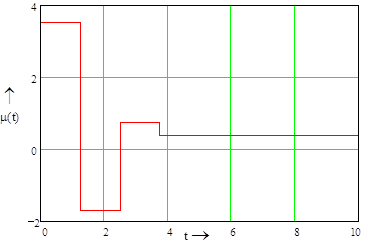
Оптимальное управляющие воздействие было найдено в пункте 5 и в координатах времени имеет следующий вид:
m(t)=3,54(h(t)-h(t-T0)) –1,703(h(t-T0)-h(t-2*T0))+ (6.1)
+0,758(h(t-2*T0)-h(t-3*T0))+0,4 h(t-3*T0),
где
h(t) – функция Хевисайда;
T0 – период квантования равный 1,25.
Тогда
m(t)=3,54(h(t)-h(t-1,25)) –1,703(h(t-1,25)-h(t-2,5))+ (6.2)
+0,758(h(t-2,5)-h(t-3,75))+0,4 h(t-3,75).
|
Рисунок 6.1 – Оптимальное управляющие воздействие.
Для нахождения реакции непрерывной линейной части на данное воздействие воспользуемся изображением Лапласа. Используя свойство линейность данного изображения и теорему запаздывания найдем, что
j(t)= 3,54(g(t) - g(t-1,25)) –1,703(g(t-1,25)-g(t-2,5))+ (6.3)
+0,758(g(t-2,5)-h(t-3,75))+0,4 h(t-3,75),
где
g(t)=f(t)h(t),
![]() – переходная функция линейной части, найденная нами в пункте 4.
– переходная функция линейной части, найденная нами в пункте 4.
Изобразим реакцию непрерывной линейной части на оптимальное управляющие воздействие.
|
Рисунок 6.2 – Реакция непрерывной линейной части на оптимальное управляющие воздействие
На этом все построения окончены.
Заключение
В данной курсовой работе был сделан синтез и анализ оптимальной одноконтурной САУ при использовании трех типов регуляторов, реализующих П-, ПИ- и ПИД-закон регулирования. Проведены сравнительный характеристики данных типов регуляторов и был сделан вывод, что ПИД-закон регулирования является наилучшим среди рассмотренных.
Были проведены расчеты по использованию данных регуляторов в цифровых системах. Как показали расчеты, несмотря на то, что цифровые системы – это системы дискретного действия и действуют через определенные промежутки времени, переходные процессы в цифровых системах не сильно отличаются от переходных процессов в непрерывных системах, а конечное состояние выходной величины одинаково. Кроме того развитие микропроцессорной техники и использование теории управления в цифровых системах позволяют создать регуляторы различной сложности и с заранее заданных свойствами. Один из регуляторов, обеспечивающий перевод системы из одного состояния в другое за минимальное число периодов квантования при наличии ограничения на управляющие воздействие, был синтезирован в данной курсовой работе.
Список литературы
1. Пугачев В.И. Методические указания по курсу: «Теория автоматического управления» для студентов всех форм обучения специальности 21.01 – автоматика и управление в технических системах. Часть I. Краснодарский политехнический институт – Краснодар, 1990. – 157 с.
2. Пугачев В.И. Методические указания по курсу: «Теория автоматического управления» для студентов всех форм обучения специальности 21.01 – автоматика и управление в технических системах. Часть III. Краснодарский политехнический институт – Краснодар, 1995. – 114 с.
3. Колосов С. П., Калмыков И. В.,Нефедова В. И. “Элементы автоматики”
издательство “Машиностроение”, Москва, 1970.
Похожие работы
... принципиальной схемы приведена в Приложении Б Рисунок 3.7 - Принципиальная электрическая схема корректирующего устройства 4. Экономический расчет Затраты на проектирование цифрового регулятора для электропривода с фазовой синхронизацией определяются по формуле: , (1.1) где Сосн, зп - основная заработная плата персонала, руб.; Сдоп, зп - дополнительная заработная плата ...
... вариант To ko T1 T2 kc kв kQ kП ky T3 k3 ν σ c c c c % % 4-9 0.7 6 0.4 0.025 2.5 0.5 200 0.13 0.2 26 0.01 2 2 5 Введение Задача синтеза системы автоматического регулирования заключается в выборе такой её структуры, параметров, характеристик и способов их реализации, ...
... ТРЕБОВАНИЙ И ПОСТАНОВКА ЗАДАЧ ПРОЕКТИРОВАНИЯ 1.1 Расчеты основных параметров электромеханической системы привода В данном курсовом проекте разрабатывается привод подач токарного станка. Для перемещения по координате предусмотрен свой привод. Поэтому разработку производим для одного контура управления. Применение ЦСУ позволяет значительно повысить точность и качество обработки, упростить ...
... правило, выполняется в виде одной «большой» ИМС. Схемотехника является частью микроэлектроники, предметом которой являются методы построения устройств различного назначения на микросхемах широкого применения. Предметом же цифровой схемотехники являются методы построения (проектирования) устройств только на цифровых ИМС. Особенностью цифровой схемотехники является широкое применение для описания ...


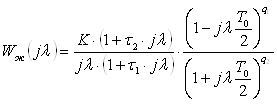
0 комментариев