Навигация
Правило 1. Если F- первообразная ф-ции f, а G- первообразная ф-ции g, то F+G является первообразная ф-ции f+g
2. Правило 1. Если F- первообразная ф-ции f, а G- первообразная ф-ции g, то F+G является первообразная ф-ции f+g.
Док-во: Воспользуемся опр-ием первообразной , т.е. найдем производную ф-ции F+G.
(F+G)¢=F¢+G¢=f+g
Правило 2. Если F- первообразная ф-ции
f, а k –постоянная , то kF- первообразная ф-ции kf.
Док-во: Воспользуемся опр-ием первообразной , т.е. найдем производную ф-ции kF.
(kF)¢=kF¢=kf
Правило 3. Если y=F(x)- первообразная ф-ции
y=f(x),а k и b- постоянные, причем k¹0 то ф-ция y=1/k*f(kx+b) явл-ся первообразной ф-ции y=f(kx+b)
Док-во: Воспользуемся опр-ием первообразной , т.е. найдем производную ф-ции y=1/k*F(kx+b)
(1/k*F(kx+b))¢=1/k*F¢(kx+b)*k=F¢(kx+b)=f(kx+b)
Билет № 18.
1.Пусть материальная точка движения по координатной прямой по закону x=x(t), т.е. координата точки – известная ф-ия времени. За промежуток времени êt перемещение точки равно êx, а средняя скорость vср=êx/êt. Если движение таково, что при êt®0 значение средней скорости стремится к некоторому определённому числу, то это число называют мгновенной скоростью (êx/êy ® vмгн, при êt®0). Но по определению производной êx/êy ® x’ при êt®0. Мгновенная скорость определена для любой дифференцируемой ф-ии, описывающей перемещение точки по прямой. Чтобы найти скорость движения v, нужно определить производную от координаты по времени, т.е. v(t)=x’(t). Пример. Координата точки, движущейся по прямой, задана формулой x(t)=2t^2-3t+1 (x(t) – перемещение в метрах, t- время в секундах). Найти скорость точки в момент времени t=2c. Имеем: v(t)=x’(t)=4t-3; v(2)=4*2-3=5 (м/с).
2. Таблица первообразных элементарных ф-ий.
| Ф-ия | y=x^n, n¹1 | y=sin x | y=cos x |
| Общий вид первообразных | (x^(n+1))/(n+1)+C | -cos x+C | Sin x+C |
| Ф-ия | y=e^x | y=a^x | Y= 1/x |
| Общий вид первообразных | e^x+C | (a)/ln a+C | ln x +C |
Для доказательства воспользуемся определением первообразной.
1) ((x^n+1))/(n+1)+C)’= (n+1)/(n+1)*x^n + C’=x^n;
2) (-cosx+C)’=sinx+C’=sinx;
3) (sinx+C)’=cosx+C’=cosx;
4) (e^n+C)’=e^x+C’=e^x;
5) ((a^x)/(ln a)+C)=1/(ln a) *ln a+C’=a^x;
6) (ln x+C)’=(1/x)+C’=1/x
Билет №19
1.Функция y=F(x) называется периодической, если существует такое число Т, не равное нулю, что для любых значений аргумента из области определения функции выполняются равенства f(x-T)=f(x)=f(x+T). Число Т называется периодом функции. Например, y=sinx – периодическая функция (синусоиду нарисуешь сам (а)) Периодом функции являются любые числа вида T=2PR, где R –целое, кроме 0. Наименьшим положительным периодом является число T=2P. Для построения графика периодической функции достаточно построить часть графика на одном из промежутков длинной Т, а затем выполнить параллельный перенос этой части графика вдоль оси абсцисс на +-Т, +-2Т, +-3Т,…
2. Если ф-ия u и v дифференцируемы в некоторой точке, то их сумма дифференцируема в этой же точке и производная суммы равна сумме производных: (u+v)’=u’+v’. Доказательство. Найдём производную суммы по определению производной.
1) Пусть задана точка x0, êx-приращение аргумента.
2) 2) Вычислим приращение ф-ии:
ê(u+v)=u(x0+êx)+(x0+êx)–(u(x0)+v(x0))=u(x0+êx)-u(x0)+v(x0+êx )- v(x0)= êu+êv.
3)Найдём отношение приращения ф-ии к приращению аргумента:
ê(u+v)/êx=(êu+êv)/êx =êu /êx +êv/êx.
4) Выясним, к чему стремится разносное отношение при êx®0
êu/êx+êvêx ®u’+v’ при êx®0
Билет №20
1)Изобразим в прямоугольной системе координат графики следующих показательных ф-ий:y=(3/2), y=2, y=(5/2), y=3
Все графики проходят через точку M(0;1).
Проведём касательные к графикам в этой точке. Измерим углы наклона касательных к оси абсцисс. У касательных к графикам ф-ии y=(3/2), y=2, y(5/2) углы с положительным направлением оси Ох меньше 45°. У касательной к графику ф-ии y=3 этот угол больше 45°. Наличие у показательной ф-ии y=e (e=2.71828…) касательной, проведёной в точке M(0;1) и образующей с положительным направлением оси абсцисс угол в 45, означает, что производная в точке х0 =0 равно 1.
Натуральным логарифмом называется логарифм по основанию е. Натуральный логарифм обозначается знаком ln, т.е. log x=ln x.
2. Если производная ф-ии положительна в каждой точке интервала, то ф-ия возрастает на этом интервале.
Доказательство: Ф-ия y= f(x) называется возрастает, если большему значению аргумента соответствует большее значение ф-ии.
Известно, что значения дифференцируемой на интеграле ф-ии, значения производной связываются формулой Лагранжа: если ф-ия y=f(x) дифференцируема на некотором промежутке, точки x1 и x2 принадлежат промежутку (x1< x2), то на интеграле (х1;х2) найдется такая точка с, для которой выполняется равенство f’(c)=(f(x2)-f(x1))/(x2-x1).
Пусть производная ф-ии принимает положительные значения на интеграле I, т.е. f’(x)>0.Возьмем два знацения аргумента x1 и x2,принадлежащие этому интегралу, причём х1<х2. Сравним значения этой ф-ии в точках х1 и х2. По формуле Лагранжда найдётся такое значения с Î (х1:х2), для которой выполняется равенство
F’(c)=(f(x2)-f(x1))/(x2-x1).
Из этого условия следует, что f(x2)-f(x1)=f’(c)*(x2-x1).
Заметим, что f(c)>0 (по условию), значит, f’(c)*(x2-x1)>0, т.е. разность значению аргумента соответствует большее значение ф-ии, т.е. ф-ия
y=f(x) является возрастающей. Аналогично показывается достаточное условия ф-ии.
Похожие работы
... и служит сырьем для цементной промышленности. Уровень развития и факторы размещения основных отраслей промышленности, сельского хозяйства и непроизводственной сферы. Экономика Республики Корея - двенадцатая экономика в мире по величине ВВП. С 1979 г. Корея проводит политику экономической открытости для зарубежных инвесторов, что привело к широкомасштабным американским, японским и ...
... ссудного капитала. Поэтому неудивительно, что в 50—60-х годах капиталовложения значительно опережали величину внутренних сбережений. (В.И. Шипаева "Южная Корея в системе мирового капиталистического хозяйства", Мир, Москва, 1994; В.К. Ломакин "Мировая экономика", Финансы, М, 1998). Таблица 1. Сбережения и капиталовложения, % к ВВП 1976 1980 1985 1990 1995 ...
... - высокая начальная стоимость разработки, отсутствие устоявшихся бизнес-процессов, требующее периодического "доведения" системы, необходимость наличия компьютеров, постоянно подключенных к Интернету. Сайты туристских агентств. Наиболее технологичными среди этих сайтов являются электронные магазины - такой вид агентских сайтов только начинает вырисовываться на современном он-лайновом туристском ...
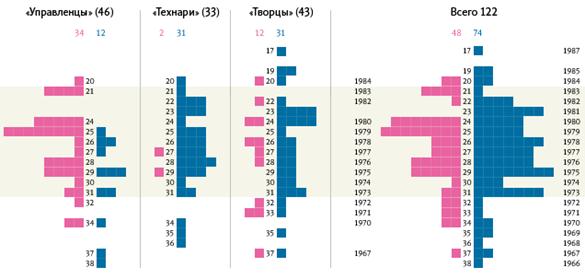
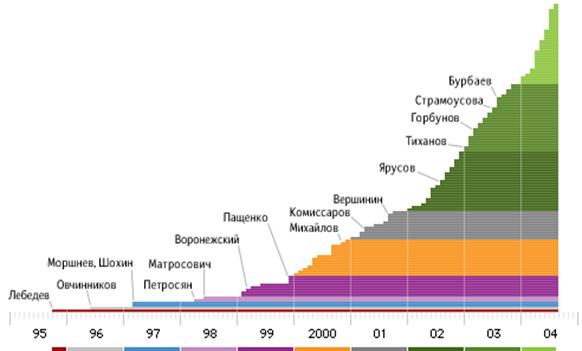
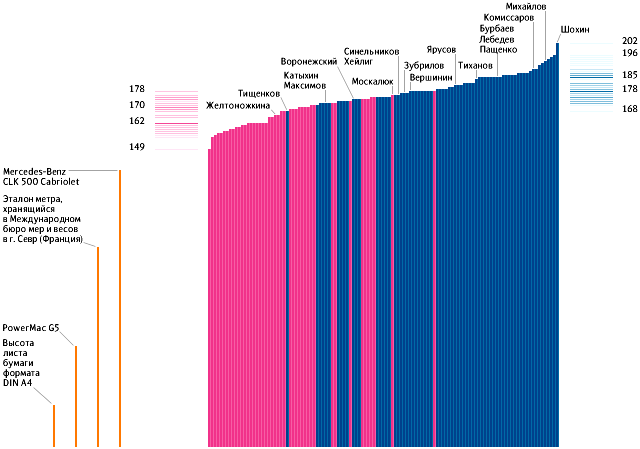
... свой профессиональный опыт. Самое важное, что удается избавиться от балласта, который неизбежно накапливается в любой организации. Глава 3. Формирование корпоративной культуры на примере Студии Артемия Лебедева 3.1. «Студия Артемия Лебедева» Студия Артемия Лебедева — крупнейшая в России компания, профессионально занимающаяся дизайном, основанная Артемием Лебедевым в 1995 году. Занимается и ...




0 комментариев