Навигация
Аксиоматика теории множеств
Содержание стр. Введение………………………………………………………………………….3
§1. Система аксиом…………………………………………………………….....4
Аксиома объемности…………………………………………………6
Аксиома пары…………………………………………………………6
Аксиома пустого множества…………………………………………6
Аксиомы существования классов……………………………………8
Аксиома объединения……………………………………………….14
Аксиома множества всех подмножеств……………………………14
Аксиома выделения………………………………………………….15
Аксиома замещения…………………………………………………16
Аксиома бесконечности……………………………………………..16
§2. Аксиома выбора. Лемма Цорна…………………………………………….19
Заключение………………………………………………………………………22 Список литературы……………………………………………………………...23
Введение
Значение математической логики в нашем и прошлом столетии сильно возросло. Главной причиной этого явилось открытие парадоксов теории множеств и необходимость пересмотра противоречивой интуитивной теории множеств. Было предложено много различных аксиоматических теорий для обоснования теории множеств, но как бы они не отличались друг от друга своими внешними чертами, общее для всех них содержание составляют те фундаментальные теоремы, на которые в своей повседневной работе опираются математики. Выбор той или иной из имеющихся теорий является в основном делом вкуса; мы же не предъявляем к системе, которой будем пользоваться, никаких требований, кроме того, чтобы она служила достаточной основой для построения современной математики.
§1. Система аксиом
Опишем теорию
первого порядка
NBG,
которая в основном
является
системой того
же типа, что и
система, предложенная
первоначально
фон Нейманом
[1925], [1928], а затем тщательно
пересмотренная
и упрощенная
Р. Робинсоном
[1937], Бернайсом
[1937—1954] и Гёделем
[1940]. (Будем в основном
следовать
монографии
Гёделя, хотя
и с некоторыми
важными отклонениями.)
Теория NBG
имеет единственную
предикатную
букву ![]() и не имеет ни
одной функциональной
буквы или предметной
константы.
Чтобы быть
ближе к обозначениям
Бернайса [1937—1954]
и Гёделя [1940], мы
будем употреблять
в качестве
переменных
вместо x1,
x2,
… прописные
латинские
буквы X1,
Х2,
... (Как
обычно, мы используем
буквы X,
Y,
Z,
... для
обозначения
произвольных
переменных.)
Мы введем также
сокращенные
обозначения
Х
и не имеет ни
одной функциональной
буквы или предметной
константы.
Чтобы быть
ближе к обозначениям
Бернайса [1937—1954]
и Гёделя [1940], мы
будем употреблять
в качестве
переменных
вместо x1,
x2,
… прописные
латинские
буквы X1,
Х2,
... (Как
обычно, мы используем
буквы X,
Y,
Z,
... для
обозначения
произвольных
переменных.)
Мы введем также
сокращенные
обозначения
Х![]() Y
для
Y
для![]() (X,
Y)
и X
(X,
Y)
и X![]() Y
для
Y
для ![]()
![]() (X,
Y).
Содержательно
знак
(X,
Y).
Содержательно
знак ![]() понимается
как символ
отношения
принадлежности.
понимается
как символ
отношения
принадлежности.
Следующим образом определим равенство:
Определение.
Х=Y
служит сокращением
для формулы
![]() .
.
Таким образом, два объекта равны тогда и только тогда, когда они состоят из одних и тех же элементов.
Определение.
![]() служит сокращением
для формулы
служит сокращением
для формулы
![]() (включение).
(включение).
Определение.
X![]() Y
служит сокращением
для Х
Y
служит сокращением
для Х ![]() Y
& X ≠
Y
(собственное
включение).
Y
& X ≠
Y
(собственное
включение).
Из этих определений легко следует
Предложение 1.
(а) ![]() Х
= Y
Х
= Y ![]() (X
(X ![]() Y
&
Y
Y
&
Y ![]() X);
X);
(b) ![]() Х
= Х;
Х
= Х;
(с) ![]() Х
= Y
Х
= Y ![]() Y
=
Х;
Y
=
Х;
(d) ![]() Х
= Y
Х
= Y ![]() (Y
= Z
(Y
= Z ![]() Х
= Z);
Х
= Z);
(е) ![]() Х
= Y
Х
= Y ![]() (Z
(Z![]() X
X ![]() Z
Z![]() Y).
Y).
Теперь приступим к перечислению собственных аксиом теории NBG, перемежая формулировки самих аксиом различными следствиями из них и некоторыми дополнительными определениями. Предварительно, однако, отметим, что в той «интерпретации», которая здесь подразумевается, значениями переменных являются классы. Классы — это совокупности, соответствующие некоторым, однако отнюдь не всем, свойствам (те свойства, которые фактически определяют классы, будут частично указаны в аксиомах. Эти аксиомы обеспечивают нам существование необходимых в математике классов и являются, достаточно скромными, чтобы из них нельзя было вывести противоречие). (Эта «интерпретация» столь же неточна, как и понятия «совокупность», «свойство» и т. д.)
Назовем класс множеством, если он является элементом какого-нибудь класса. Класс, не являющийся множеством, назовем собственным классом.
Определение.
M(X)
служит сокращением
для ![]() Y(X
Y(X![]() Y)
(X есть множество).
Y)
(X есть множество).
Определение.
Pr(X)
служит сокращением
для ![]() M(X)
(X
есть собственный
класс).
M(X)
(X
есть собственный
класс).
В дальнейшем увидим, что обычные способы вывода парадоксов приводят теперь уже не к противоречию, а всего лишь к результату, состоящему в том, что некоторые классы не являются множествами. Множества предназначены быть теми надежными, удобными классами, которыми математики пользуются в своей повседневной деятельности; в то время как собственные классы мыслятся как чудовищно необъятные собрания, которые, если позволить им быть множествами (т. е. быть элементами других классов), порождают противоречия.
Система NBG задумана как теория, трактующая о классах, а не о предметах. Мотивом в пользу этого послужило то обстоятельство, что математика не нуждается в объектах, не являющихся классами, вроде коров или молекул. Все математические объекты и отношения могут быть выражены в терминах одних только классов. Если же ради приложений в других науках возникает необходимость привлечения «неклассов», то незначительная модификация системы NBG позволяет применить ее равным образом как к классам, так и к «неклассам» (Мостовский [1939]).
Мы введем
строчные латинские
буквы x1,
x2,
… в качестве
специальных,
ограниченных
множествами,
переменных.
Иными словами,
![]() x1
A
(x1)
будет служить
сокращением
для
x1
A
(x1)
будет служить
сокращением
для ![]() X
(M(X)
X
(M(X)![]() A
(X))
, что содержательно
имеет следующий
смысл: «A
истинно для
всех множества,
и
A
(X))
, что содержательно
имеет следующий
смысл: «A
истинно для
всех множества,
и ![]() x1
A
(x1)
будет служить
сокращением
для
x1
A
(x1)
будет служить
сокращением
для ![]() X
(M(X)
X
(M(X)![]() A
(X)),
что содержательно
имеет смысл:
«A истинно для
некоторого
множества».
Заметим, что
употребленная
в этом определении
переменная
X
должна быть
отличной от
переменных,
входящих в A
(x1).
(Как и обычно,
буквы х,
y,
z,
... будут
употребляться
для обозначения
произвольных
переменных
для множеств.)
A
(X)),
что содержательно
имеет смысл:
«A истинно для
некоторого
множества».
Заметим, что
употребленная
в этом определении
переменная
X
должна быть
отличной от
переменных,
входящих в A
(x1).
(Как и обычно,
буквы х,
y,
z,
... будут
употребляться
для обозначения
произвольных
переменных
для множеств.)
П р и м е р.
Выражение
![]() Х
Х![]() х
х![]() y
y![]() ZA
(X, х, y,
Z)
служит сокращением
для
ZA
(X, х, y,
Z)
служит сокращением
для
![]() Х
Х![]() Xj
(М(Xj)
Xj
(М(Xj)![]()
![]() Y(M(Y)&
Y(M(Y)&![]() ZA
(X,
Xj,
Y,
Z))).
ZA
(X,
Xj,
Y,
Z))).
А
к с и о м а Т. (Аксиома
объемности.)
Х = Y ![]() (X
(X![]() Z
Z![]() Y
Y![]() Z).
Z).
Предложение 2. Система NBG является теорией первого порядка с равенством.
А к с и о м а Р. (Аксиома
пары.) ![]() x
x![]() y
y![]() z
z![]() u
(u
u
(u ![]() z
z ![]() u
= x
u
= x![]() u
= y), т. е.
для любых множеств
х и у
существует
множество z
такое, что х
и у
являются
единственными
его элементами.
u
= y), т. е.
для любых множеств
х и у
существует
множество z
такое, что х
и у
являются
единственными
его элементами.
А к с и о м а N. (Аксиома
пустого множества.) ![]() х
х ![]() y
(у
y
(у ![]() х), т. е.
существует
множество, не
содержащее
никаких элементов.
х), т. е.
существует
множество, не
содержащее
никаких элементов.
Из аксиомы N и аксиомы объемности следует, что существует лишь единственное множество, не содержащее никаких элементов, т. е.
![]()
![]() 1x
1x
![]() y
(у
y
(у ![]() х). Поэтому
мы можем ввести
предметную
константу 0,
подчиняв ее
следующему
условию.
х). Поэтому
мы можем ввести
предметную
константу 0,
подчиняв ее
следующему
условию.
Определение. ![]() y
(y
y
(y
![]() 0).
0).
Так как выполнено условие единственности для неупорядоченной пары, то можем ввести новую функциональную букву g(х, y) для обозначения неупорядоченной пары х и у. Впрочем вместо g(х, y) мы будем писать {х, у}. Заметим, что можно однозначно определить пару {X, Y} для любых двух классов Х и Y, а не только для множеств х и у. Положим {X, Y} = 0, если один из классов X, Y не является множеством. Можно доказать, что
![]() NBG
NBG![]() 1Z((M(X)&M(Y)&
1Z((M(X)&M(Y)&![]() u
(u
u
(u ![]() Z
Z ![]() u
= X
u
= X
![]() u
= Y))
u
= Y))
![]()
![]() ((
(( ![]() M(X)
M(X) ![]()
![]() M(Y))&Z=0)).
M(Y))&Z=0)).
Этим оправдано введение пары {X, Y}:
Определение.
(М(Х)
& М(Y)
&![]() u
(и
u
(и ![]() {X,
Y}
{X,
Y} ![]() u
= X
u
= X
![]() u
= Y))
u
= Y))
![]()
![]() ((
((![]() M(X)
M(X)![]()
![]() M(Y))
& {X,
Y}
= 0).
M(Y))
& {X,
Y}
= 0).
Можно
доказать, что
![]() NBG
NBG![]() x
x
![]() y
y
![]() u
(u
u
(u ![]() {х,
у}
{х,
у} ![]() u
= x
u
= x
![]() u
= y)
и
u
= y)
и
![]() NBG
NBG![]() x
x
![]() y
(M({х,
у})).
y
(M({х,
у})).
Определение.
![]() = {{Х}, {X, Y}}.
= {{Х}, {X, Y}}. ![]() называется
упорядоченной
парой
классов Х
и Y.
называется
упорядоченной
парой
классов Х
и Y.
Никакого внутреннего интуитивного смысла это определение не имеет. Оно является лишь некоторым удобным способом (его предложил Ку-ратовский) определить упорядоченные пары таким образом, чтобы можно было доказать следующее предложение, выражающее характеристическое свойство упорядоченных пар.
Предложение 3.
![]() NBG
NBG![]() x
x
![]() y
y
![]() u
u
![]() v
(
v
(![]() ).
).
Доказательство. Пусть ![]() =
= ![]() .
Это значит,
что {{x},
{x,
y}}
= {{u},
{u,
v}}.
Так как {х}
.
Это значит,
что {{x},
{x,
y}}
= {{u},
{u,
v}}.
Так как {х} ![]() {{x},
{x,
y}},
то {x}
{{x},
{x,
y}},
то {x} ![]() {{u},
{u,
v}}.
Поэтому
{x}
= ={u}
или {х}
= {u,
v}.
В обоих
случаях х
= и. С другой
стороны, {u,
v}
{{u},
{u,
v}}.
Поэтому
{x}
= ={u}
или {х}
= {u,
v}.
В обоих
случаях х
= и. С другой
стороны, {u,
v} ![]() {{u},
{u,
v}}
и, следовательно,
{u,
v}
{{u},
{u,
v}}
и, следовательно,
{u,
v} ![]() {{x},
{x,
y}}.
Отсюда
{u,
v}
= {x}
или {u,
v}
= ={x,
y}.
Подобным же
образом {x,
y}
= {u}
или {х, у}={и,
v}.
Если или {u,
v}
= ={x}
и {х,
y}
= {u},
то х = и
= у = v,
в противном
случае {и,
v}
= {х, у} и, следовательно,
{и, v}
= {u,
у}. Если при
этом v
≠ u,
то y
= v,
если же v
= u,
то тоже y
= v.
Итак, в любом
случае, y
= v.
{{x},
{x,
y}}.
Отсюда
{u,
v}
= {x}
или {u,
v}
= ={x,
y}.
Подобным же
образом {x,
y}
= {u}
или {х, у}={и,
v}.
Если или {u,
v}
= ={x}
и {х,
y}
= {u},
то х = и
= у = v,
в противном
случае {и,
v}
= {х, у} и, следовательно,
{и, v}
= {u,
у}. Если при
этом v
≠ u,
то y
= v,
если же v
= u,
то тоже y
= v.
Итак, в любом
случае, y
= v.
Мы теперь обобщим понятие упорядоченной пары до понятия упорядоченной n-ки.
Определение
![]() =
Х,
=
Х,
![]()
Так, например,
![]() и
и ![]()
В дальнейшем
индекс NBG
в записи
![]() NBGопускается.
NBGопускается.
Нетрудно доказать следующее обобщение предложения 3:
![]()
![]()
Аксиомы существования классов.
Эти аксиомы утверждают, что для некоторых свойств, выраженных формулами, существуют соответствующие классы всех множеств, обладающих этими свойствами.
А к с и о м а
В1. ![]() X
X ![]() u
u
![]() v
(
v
(![]()
![]() X
X ![]() u
u ![]() v) (
v) (![]() -
отношение).
-
отношение).
А к с и о м а
В2. ![]() X
X
![]() Y
Y ![]() Z
Z
![]() u
(u
u
(u ![]() Z
Z ![]() u
u ![]() X
& u
X
& u ![]() Y)
Y)
(пересечение).
А к с и о м а
В3. ![]() X
X ![]() Z
Z ![]() u
(u
u
(u ![]() Z
Z ![]() u
u
![]() X) (дополнение).
X) (дополнение).
А к с и о м а
В4. ![]() X
X ![]() Z
Z ![]() u
(u
u
(u ![]() Z
Z ![]()
![]() v
(
v
(![]()
![]() X)) (область
X)) (область
определения).
А к с и о м а
В5.
![]() X
X ![]() Z
Z ![]() u
u
![]() v
(
v
(![]()
![]() Z
Z ![]() u
u ![]() X).
X).
А к с и о м а
В6.
![]() X
X ![]() Z
Z ![]() u
u
![]() v
v
![]() w
(
w
(![]()
![]() Z
Z ![]()
![]()
![]() X).
X).
А к с и о м а
В7.
![]() X
X ![]() Z
Z ![]() u
u
![]() v
v
![]() w
(
w
(![]()
![]() Z
Z ![]()
![]()
![]() X).
X).
С помощью аксиом В2—В4 можно доказать
![]()
![]() X
X ![]() Y
Y ![]() 1Z
1Z ![]() u
(u
u
(u ![]() Z
Z ![]() u
u ![]() X & u
X & u ![]() Y),
Y),
![]()
![]() X
X ![]() 1Z
1Z![]() u
(u
u
(u ![]() Z
Z ![]() u
u ![]() x),
x),
![]()
![]() X
X ![]() 1Z
1Z![]() u
(u
u
(u ![]() Z
Z ![]()
![]() v
(
v
(![]()
![]() X)).
X)).
Эти результаты оправдывают введение новых функциональных букв ∩, −, D.
Определения
![]() u
(u
u
(u ![]() X
∩ Y
X
∩ Y ![]() u
u ![]() X
& u
X
& u ![]() Y) (пересечение
классов
Х и Y).
Y) (пересечение
классов
Х и Y).
![]() u
(u
u
(u ![]()
![]()
![]() u
u
![]() X) (дополнение
к классу
X).
X) (дополнение
к классу
X).
![]() u
(u
u
(u ![]() D
(X)
D
(X) ![]()
![]() v
(
v
(![]()
![]() X)) (область
определения
класса X).
X)) (область
определения
класса X).
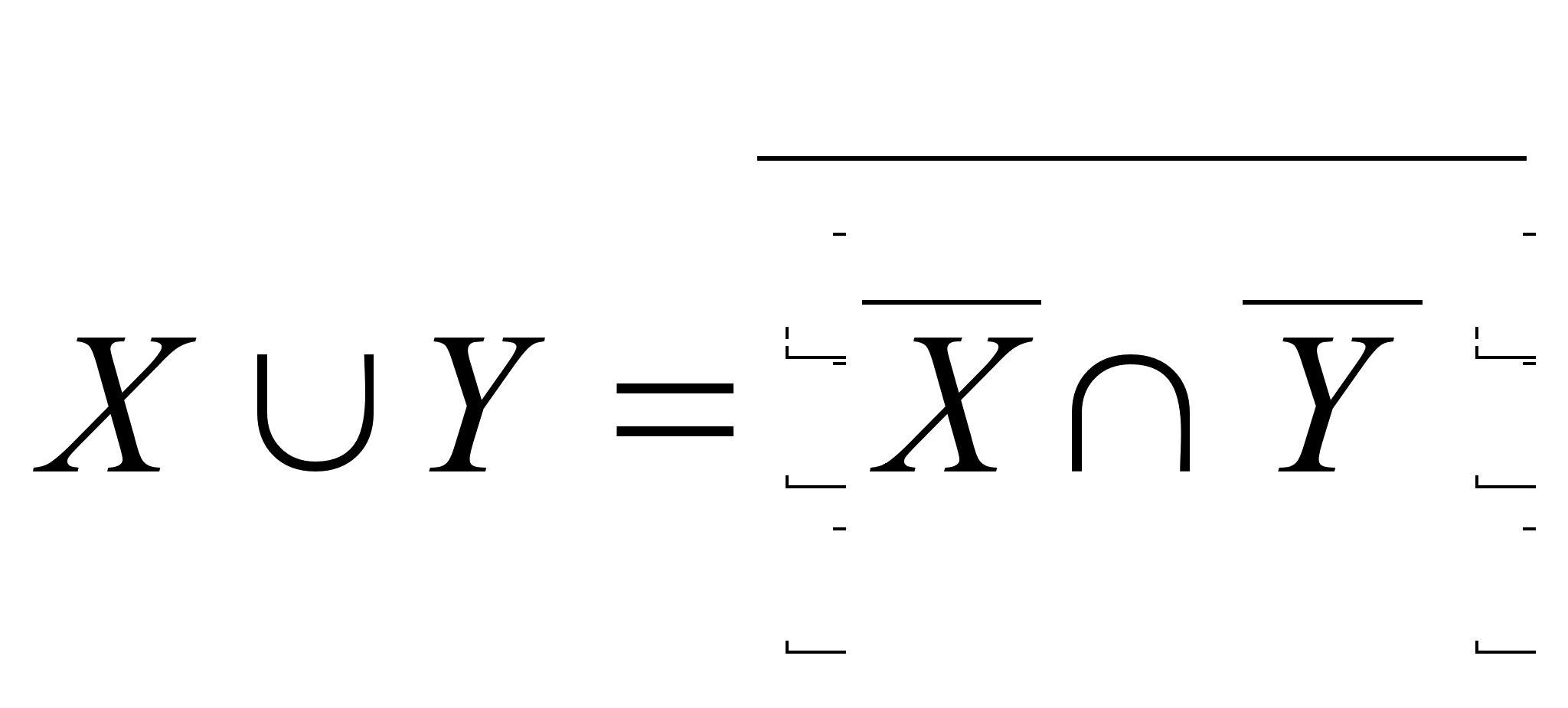 (объединение
классов
Х и Y).
(объединение
классов
Х и Y).
V
= ![]() (универсальный
класс).
(универсальный
класс).
X
− Y
= X
∩ ![]()
Общая теорема о существовании классов.
Предложение 4. Пусть φ (X1,…,Xn, Y1,…, Ym) – формула, переменные которой берутся лишь из числа X1,…,Xn, Y1,…, Ym. Назовём такую формулу предикативной, если в ней связными являются только переменные для множеств (т.е. если она может быть приведена к такому виду с помощью принятых сокращений). Для всякой предикативной формулы φ (X1,…,Xn, Y1,…, Ym)
![]()
![]() Z
Z![]() x1
…
x1
…![]() xn
(
xn
(![]()
![]() Z
Z ![]() φ (x1,…,xn,
Y1,…,
Ym)).
φ (x1,…,xn,
Y1,…,
Ym)).
Доказательство.
Мы можем ограничиться
рассмотрением
только таких
формул φ,
которые не
содержат подформул
вида Yi![]() W,
так как всякая
такая подформула
может быть
заменена на
W,
так как всякая
такая подформула
может быть
заменена на
![]() x
(x
= Yi& x
x
(x
= Yi& x ![]() W),
что в свою
очередь эквивалентно
формуле
W),
что в свою
очередь эквивалентно
формуле ![]() x
(
x
(![]() z
(z
z
(z ![]() x
x ![]() z
z ![]() Yi)
& x
Yi)
& x ![]() W).
Можно также
предполагать,
что в φ
не содержатся
подформулы
вида X
W).
Можно также
предполагать,
что в φ
не содержатся
подформулы
вида X![]() X,
которые могут
быть заменены
на
X,
которые могут
быть заменены
на ![]() u
(u
= X
& u
u
(u
= X
& u ![]() X),
последнее же
эквивалентно
X),
последнее же
эквивалентно
![]() u
(
u
(![]() z
(z
z
(z ![]() u
u ![]() z
z ![]() X)
& u
X)
& u ![]() X).
Доказательство
проведем теперь
индукцией
по числу k
логических
связок и кванторов,
входящих в
формулу φ
(записанную
с ограниченными
переменными
для множеств).
X).
Доказательство
проведем теперь
индукцией
по числу k
логических
связок и кванторов,
входящих в
формулу φ
(записанную
с ограниченными
переменными
для множеств).
1. Пусть k
= 0. Формула φ
имеет вид xi![]() xj,
или xj
xj,
или xj![]() xi,
или xi
xi,
или xi![]() Yi,
где 1 ≤ i
< j
≤ n.
В первом случае,
по аксиоме В1,
существует
некоторый класс
W1
такой, что
Yi,
где 1 ≤ i
< j
≤ n.
В первом случае,
по аксиоме В1,
существует
некоторый класс
W1
такой, что
![]() xi
xi![]() xj
(
xj
(![]()
![]() W1
W1![]() xi
xi![]() xj).
xj).
Во втором случае, по той же аксиоме, существует класс W2 такой, что
![]() xi
xi![]() xj(
xj(![]()
![]() W2
W2![]() xj
xj![]() xi),
xi),
и тогда, в силу
![]()
![]() X
X![]() Z
Z
![]() u
u
![]() v
(
v
(![]()
![]() Z
Z ![]()
![]()
![]() X),
X),
существует класс W3 такой, что
![]() xi
xi![]() xj(
xj(![]()
![]() W3
W3![]() xj
xj![]() xi).
xi).
Итак, в любом из первых двух случаев существует класс W3 такой, что
![]() xi
xi![]() xj(
xj(![]()
![]() W
W ![]() φ (x1,…,xn,
Y1,…,
Ym)).
φ (x1,…,xn,
Y1,…,
Ym)).
Тогда, заменив в
![]()
![]() X
X![]() Z
Z ![]() v1…
v1…![]() vk
vk![]() u
u![]() w
(
w
(![]()
![]() Z
Z ![]()
![]()
![]() X)
X)
X на W, получим, что существует некоторый класс Z1 такой, что
![]() x1…
x1… ![]() xi-1
xi-1![]() xi
xi![]() xj
(
xj
(![]()
![]() Z1
Z1![]() φ
(x1,…,xn,
Y1,…,
Ym)).
φ
(x1,…,xn,
Y1,…,
Ym)).
Далее, на основании
![]()
![]() X
X![]() Z
Z ![]() v1…
v1…![]() vm
vm![]() x1…
x1…![]() xn
(
xn
(![]()
![]()
![]() Z
Z![]()
![]()
![]() X)
X)
там же при Z1 = X, заключаем, что существует класс Z2 такой, что
![]() x1
…
x1
… ![]() xi
xi
![]() xi+1
…
xi+1
… ![]() xj
(
xj
(![]()
![]() Z2
Z2![]() φ
(x1,…,xn,
Y1,…,
Ym)).
φ
(x1,…,xn,
Y1,…,
Ym)).
Наконец, применяя
![]()
![]() X
X![]() Z
Z ![]() v1…
v1…![]() vm
vm![]() x1…
x1…![]() xn
(
xn
(![]()
![]() Z
Z ![]()
![]()
![]() X)
X)
(1)
там же при Z2 = Х, получаем, что существует класс Z такой, что
![]() x1…
x1…![]() xn
(
xn
(![]()
![]() Z
Z ![]() φ (x1,…,xn,
Y1,…,
Ym)).
φ (x1,…,xn,
Y1,…,
Ym)).
Для остающегося
случая xi![]() Yi
теорема
следует из (1)
и
Yi
теорема
следует из (1)
и
![]()
![]() X
X![]() Z
Z ![]() x
x![]() v1…
v1…![]() vm
(
vm
(![]()
![]() Z
Z ![]() x
x ![]() X).
X).
Похожие работы
... действительных чисел. 3.3. Конечные и бесконечные множества Конечное множество - множество, состоящее из конечного числа элементов. Пример. A = {1, 2, 3, 4, 5}. Основной характеристикой конечного множества является число его элементов. Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из ...
... нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, она просто не в силах это сделать. Еще пример, выпадение снега в Москве 30 ноября является ...
... понятия вероятности задача некоторой несостоятельности классического определения вероятности была решена. Однако наблюдаются попытки дать трактовку вероятности с более широких позиций, в том числе и с позиций теории информации. 2. Динамика развития понятия математического ожидания 2.1 Предпосылки введения понятия математического ожидания Одним из первых приблизился к определению понятия ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
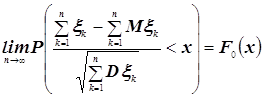
0 комментариев