Навигация
Алгебра и начала анализа. | |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
|
| Ответ |
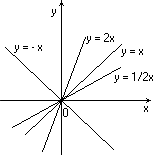
Ответ №2. Опр. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax2 + bx + c, где х - независимая переменная, а, b и с - некоторые числа, причем а ![]() 0.
0.
Графиком квадратичной функции является парабола.
Свойства функции y = ax2(частный случай) при а > 0.
1. Если х = 0, то y = 0. График функции проходит через начало координат.
2. Если х ![]() 0, то y > 0. График функции расположен в верхней полуплоскости.
0, то y > 0. График функции расположен в верхней полуплоскости.
3. График функции симметричен относительно оси Oy.
4. Функция убывает в промежутке (- ![]() ; 0] и возрастает в промежутке [0; +
; 0] и возрастает в промежутке [0; + ![]() ).
).
5. Наименьшее значение функция принимает при х = 0. Область значений функции [0; + ![]() ).
).
Свойства функции y = ax2 при а < 0.
1. Если х = 0, то y = 0. График функции проходит через начало координат.
2. Если х ![]() 0, то y < 0. График функции расположен в нижней полуплоскости.
0, то y < 0. График функции расположен в нижней полуплоскости.
3. График функции симметричен относительно оси Oy.
4. Функция убывает в промежутке [0; + ![]() ) и возрастает в промежутке (-
) и возрастает в промежутке (- ![]() ; 0].
; 0].
5. Наименьшее значение функция принимает при х = 0. Область значений функции (- ![]() ; 0].
; 0].
И, так, график функции y = ax2 + bx + c есть парабола, вершиной которой является точка (m; n), где m = ![]() , n=
, n= ![]() . Осью симметрии параболы служит прямая х = m, параллельная оси y. При а > 0 ветви параболы направлены вверх, при a < 0 - вниз.
. Осью симметрии параболы служит прямая х = m, параллельная оси y. При а > 0 ветви параболы направлены вверх, при a < 0 - вниз.
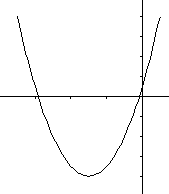
Ответ 3
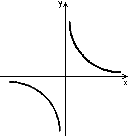
Если переменная у обратно пропорциональна переменной х, то эта зависимость выражается формулой ![]() , где
, где ![]() - коэффициент обратной пропорциональности.
- коэффициент обратной пропорциональности.
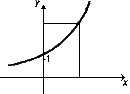
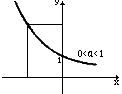
№ 4. Опр. Функция, заданная формулой y = ax, где а - некоторое положительное число, не равное еденице, называется показательной.
1. Функция y = ax при а>1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то ax > 1;
е) если х < 0, то 0< ax <1;
2. Функция y = ax при 0< а <1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0< ax <1;
е) если х < 0, то ax > 1.
№5.Опр. Функцию, заданную формулой y = loga x называют логарифмической функцией с основанием а.
Свойства функции y = loga x при a>1:
а) D(f) = R+;
б) E(f) = R;
в) функция возрастает;
г) если x = 1, то loga x = 0;
д) если 0<x<1, то loga x < 0;
е) если x > 1, то loga x > 0.
Свойства функции y = loga x при 0<a<1:
а) D(f) = R+;
б) E(f) = R;
в) функция убывает;
г) если x = 1, то loga x = 0;
д) если 0 < x < 1, то loga x > 0;
е) если x > 1, то loga x < 0.
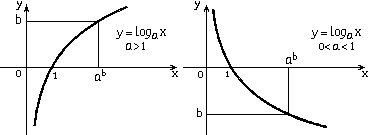
№6. Опр. Отношение катета прямоугольного треугольника, противолежащего острому углу, к гипотенузе называется синусом этого угла (обозначается sin ![]() ).
).
![]()
№ 7.Опр. Отношение катета прямоугольного треугольника, прилежащего к острому углу, к гипотенузе называется косинусом этого угла (обозначается cos ![]() )
)
№8.Опр. Отношение катета, противолежащего острому углу прямоугольного треугольника, к катету, прилежащему к этому углу, называется тангенсом (обозначается tg ![]() ).
).
№9.Опр. Отношение катета, прилежащего острому углу прямоугольного треугольника, к катету, противолежащему к этому углу, называется котангенсом (обозначается ctg ![]() )
)
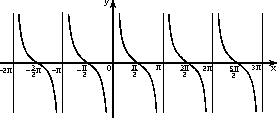
Ответ № 10
Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией. Из определения арифметической прогрессии следует, что разность между любым ее членом и ему предшествующим равна одному и тому же числу, т. е. а2 - а1 = а3 - а2 = ... = ak - ak-1 = ... . Это число называется разностью арифметической прогрессии и обычно обозначается буквой d. Для того чтобы задать арифметическую прогрессию (аn), достаточно знать ее первый член а1 и разность d. Если разность арифметической прогрессии - положительное число, то такая прогрессия является возрастающей; если отрицательное число, то убывающей. Если разность арифметической прогрессии равна нулю, то все ее члены равны между собой и прогрессия является постоянной последовательностью. Характеристическое свойство арифметической прогрессии. Последовательность (аn) является арифметической прогрессией тогда и только тогда, когда любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, т. е.Ответ № 11
Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией. Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. b2:b1 = b3:b2 = ... = bn:bn-1 = bn+1:bn = ... . Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q. Для того, чтобы задать геометрическую прогрессию (bn), достаточно знать ее первый член b1 и знаменатель q. Если q > 0 (Сумма бесконечной геометрической прогресси при ![]()
№ 12
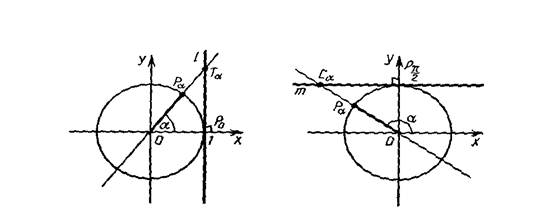
Решение тригонометрических уравнений вида sin(x) = a
формула для корней уравнения sin(x) = a, гдеЧастные случаи: sin(x) = 0, x =
Решение тригонометрических неравенств вида sin(x) > a, sin(x) < a
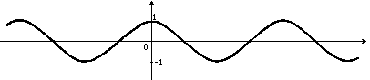
Неравенства, содержащие переменную только под знаком тригонометрической функции, называются тригонометрическими. При решении тригонометрических неравенств используют свойство монотонности триго-нометрических функций, а также промежутки их знакопостоянства. Для решения простейших тригонометрических неравенств вида sin(x) > a (sin(x) < а) используют единичную окружность или график функции y = sin(x).sin(x) = 0 если х =
sin(x) = -1, если x =
sin(x) > 0, если
sin(x) < 0, если
Ответ № 13
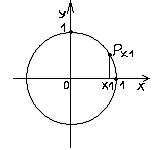
Решение тригонометрического уравнения cos(x) = a
Формула для корней уравнения cos(x) = a, гдеcos(x) = 1, x =
cos(x) = 0,
cos(x) = -1, x =
Решение тригонометрических неравенств вида cos(x) > a, cos(x) < a
Для решения простейших тригонометрических неравенств вида cos(x) > a, cos(x) < a используют единичную окружность или график функции y = cos(x); Важным моментом является знание, что:cos(x) = 0, если
cos(x) = -1, если x =
cos(x) = 1, если x =
cos(x) > 0, если
cos(x) > 0, если
№ 14
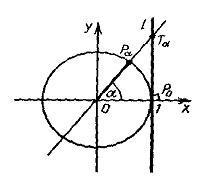
Решение тригонометрического уравнения tg(x) = a
Формула для корней уравнения tg(x) = a имеет вид:tg(x) = 0, x =
tg(x) = 1,
tg(x) = -1,
Решение тригонометрических неравенств вида tg(x) > a, tg(x) < a
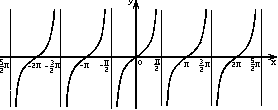
Для решения простейших тригонометрических неравенств вида tg(x) > a, tg(x) < a используют единичную окружность или график функции y = tg(x). Важно знать, что:tg(x) > 0, если
tg(x) < 0, если
Тангенс не существует, если
№ 15
Формулами приведения называются соотношения, с помощью которых значения тригонометрических функций аргументов| Функция | Аргумент | |||||||
|
|
|
|
|
|
|
|
| |
| sin | cos | cos | sin | -sin | -cos | -cos | -sin | sin |
| cos | sin | -sin | -cos | -cos | -sin | sin | cos | cos |
| tg | ctg | -ctg | -tg | tg | ctg | -ctg | -tg | tg |
| ctg | tg | -tg | -ctg | ctg | tg | -tg | -ctg | ctg |
a) при переходе от функций углов
при переходе от функций углов
б) считая
Все вышеприведенные формулы можно получить, пользуясь следующим правилом:
Любая тригонометрическая функция угла 90°n + ![]() по абсолютной величине равна той же функции угла
по абсолютной величине равна той же функции угла ![]() , если число n - четное, и дополнительной функции, если число n - нечетное. При этом, если функция угла 90°n +
, если число n - четное, и дополнительной функции, если число n - нечетное. При этом, если функция угла 90°n + ![]() . положительна, когда
. положительна, когда ![]() - острый угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
- острый угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
№ 16
Формулы косинуса суммы и разности двух аргументов: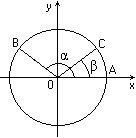
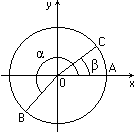
Рис.1 Рис.2
Повернем радиус ОА, равный R, около точки О на угол
Похожие работы
... b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным. Переменные a, b, c, …, k, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры. Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n а неизвестные – буквами x, y,z. ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
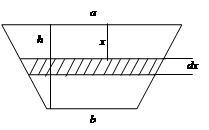
... они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала. 2.2. Изучение свойств определенного интеграла с помощью физических моделей При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
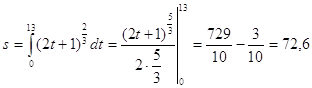





0 комментариев