Навигация
Эти же координаты имеют соответственно и векторы
Выразим скалярное произведение
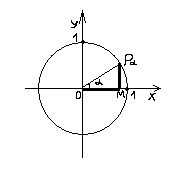
х1 = R cos
Подставив значения х1, х2, y1, y2 в правую часть равенства (1), получим:
С другой стороны, по теореме о скалярном произведении векторовимеем:
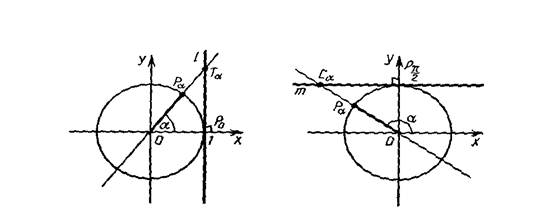
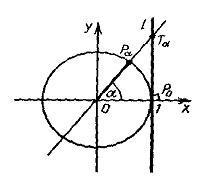
Угол ВОС между векторами
Т.к.
cos(
cos(
Значит,
cos(
sin(
Значит,
sin(
sin(
Значит,
sin(
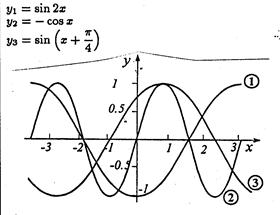
№ 17
Формулы двойных углов
Формулы сложения позволяют выразить sin 2![]() , cos 2
, cos 2![]() , tg 2
, tg 2![]() , ctg 2
, ctg 2![]() через тригонометрические функции угла
через тригонометрические функции угла ![]() .
.
Положим в формулах
sin(![]() +
+ ![]() ) = sin
) = sin![]() cos
cos![]() + cos
+ cos![]() sin
sin![]() ,
,
cos(![]() +
+ ![]() ) = cos
) = cos![]() cos
cos![]() - sin
- sin![]() sin
sin![]() ,
,![]() ,
,![]() .
.![]() равным
равным ![]() . Получим тождества:
. Получим тождества:
sin 2![]() = 2 sin
= 2 sin ![]() cos
cos ![]() ;
;
cos 2![]() = cos2
= cos2 ![]() - sin2
- sin2 ![]() = 1 - sin2
= 1 - sin2 ![]() = 2 cos2
= 2 cos2 ![]() - 1;
- 1;![]() ;
; ![]() .
.
№ 18
Формулы половинного аргумента
Выразив правую часть формулы cos 2cos 2
Если в данных соотношениях положить
cos
№ 19
Формулы суммы и разности синусов, косинусов
Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций. Формулы, на которых основано такое преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin ![]() + sin
+ sin ![]() , положим
, положим ![]() = x + y и
= x + y и ![]() = x - y и воспользуемся формулами синуса суммы и синуса разности. Получим:
= x - y и воспользуемся формулами синуса суммы и синуса разности. Получим:
sin ![]() + sin
+ sin ![]() = sin (x + y) + sin (x - y) = sinx cosy + cosx siny + sinx cosy - cosx siny = 2sinx cosy.
= sin (x + y) + sin (x - y) = sinx cosy + cosx siny + sinx cosy - cosx siny = 2sinx cosy.
Решив теперь систему уравнений ![]() = x + y,
= x + y, ![]() = x - y относительно x и y, получим х =
= x - y относительно x и y, получим х = ![]() , y =
, y = ![]() .
.
Следовательно,
sin ![]() + sin
+ sin ![]() = 2 sin
= 2 sin![]() cos
cos![]() .
.
Аналогичным образом выводят формулы:
sin ![]() -sin
-sin ![]() = 2 cos
= 2 cos![]() sin
sin ![]() ;
;
cos ![]() + cos
+ cos ![]() = 2 cos
= 2 cos![]() cos
cos![]() ;
;
cos ![]() + cos
+ cos ![]() = -2 sin
= -2 sin![]() sin
sin ![]() .
.
№ 20
Чтобы найти решение приведенного квадратного уравнения x2 + px + q = 0, где ![]() , достаточно перенести свободный член в правую часть и к обеем частям равенства прибавить
, достаточно перенести свободный член в правую часть и к обеем частям равенства прибавить ![]() . Тогда левая часть станет полным квадратом, и мы получаем равносильное уравнение
. Тогда левая часть станет полным квадратом, и мы получаем равносильное уравнение ![]() =
= ![]() - q .
- q .
Оно отличается от простейшего уравнения x2 = m только внешним видом: ![]() стоит вместо x и
стоит вместо x и ![]() - q - вместо m. Находим
- q - вместо m. Находим ![]() =
= ![]() . Отсюба х = -
. Отсюба х = - ![]()
![]() . Эта формула показывает, что всякое квадратное уравнение имеет два корня. Но эти корни могут быть и мнимыми, если
. Эта формула показывает, что всякое квадратное уравнение имеет два корня. Но эти корни могут быть и мнимыми, если ![]() < q . Может также оказаться, что оба корня квадратного уравнения равны между собой, если
< q . Может также оказаться, что оба корня квадратного уравнения равны между собой, если ![]() = q . Возращаемся к обычному виду
= q . Возращаемся к обычному виду ![]() .
.
1. Сумма корней приведенного квадратного уравнения x2 + px + q = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е. х1 + х2 = -р, а х1х2 = q .
2. Теорема, обратная теореме Виета. Если р, q, х1, х2 таковы, что х1 + х2 = -р и х1х2 = q , то х1 и х2 - корни уравнения x2 + px + q = 0.
№ 21
Опр. Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобыполучить число b.
Формулу ![]() (где b > 0, a > 0 и a
(где b > 0, a > 0 и a ![]() 1) называют основным логарифмическим тождеством.
1) называют основным логарифмическим тождеством.
Свойства логарифмов:
Для доказательства воспользуемся основным логарифмическим тождеством:
x =
Перемножим почленно эти равенства, получаем:
xy =
Следовательно, по определению логарифма (п.3) доказан. Логарифм частного равен логарифму делимого без логарифма делителя:
Ход доказательства аналогичен доказательству п.3 Логарифм степени равен произведению показателя степени на логарифм ее основания:
При доказательстве, также необходимо воспользоваться основным логарифмическим тождеством.
№ 22
Производной функции f(x) в точке х0 называется предел отношения приращения№ 23
Производная суммы равна сумме производных, если они существуют:Похожие работы
... b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным. Переменные a, b, c, …, k, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры. Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n а неизвестные – буквами x, y,z. ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала. 2.2. Изучение свойств определенного интеграла с помощью физических моделей При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
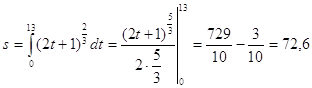





0 комментариев