Навигация
В силу соотношения (2), получим
2. В силу соотношения (2), получим
(x + 1)2=(2x – 5)2, или x2 + 2x + 1=4x2 – 20x + 25
x2 – 4x2 +2x+1 + 20x – 25=0
-3x2 + 22x – 24=0|(:-1)
3x2 – 22x + 24=0
D/4=121-3 24=121 – 72=49>0 уравнение имеет 2 различных корня.
x1=(11 – 7 )/3=11/3
x2=(11 + 7 )/3=6
Как показывает решение, корнями данного уравнения также являются числа 11/3 и 6
Ответ: x1=6, x2=11/3
Пример 5. Решим уравнение (2x + 3)2=(x – 1)2.
Учитывая соотношение (2), получим, что |2x + 3|=|x – 1|, откуда по образцу предыдущего примера(и по соотношению (1)):
2х + 3=х – 1 или 2х + 3=-х + 1
2х – х=-1 – 3 2х+ х=1 – 3
х=-4 х=-0,(6)
Таким образом корнями уравнения являются х1=-4, и х2=-0,(6)
Ответ: х1=-4, х2=0,(6)
Пример 6. Решим уравнение |x – 6|=|x2 – 5x + 9|
Пользуясь соотношением (1), получим:
х – 6=х2 – 5х + 9 или х – 6 = -(х2 – 5х + 9)
-х2 + 5х + х – 6 – 9=0 |(-1) x – 6=-x2 + 5x - 9
x2 - 6x + 15=0 x2 – 4x + 3=0
D=36 – 4 15=36 – 60= -24 <0 D=16 – 4 3=4 >02 р.к.
корней нет.
x1=(4- 2 ) /2=1
x2=(4 + 2 ) /2=3
Проверка: |1 – 6|=|12 – 5 1 + 9| |3 – 6|=|32 – 5 3 + 9|
5 = 5(И) 3 = |9 – 15 + 9|
3 = 3(И)
Ответ: x1=1; x2=3
4.2.Использование геометрической интерпритации модуля для решения уравнений.Геометрический смысл модуля разности величин-это расстояние между ними. Например, геометрический смысл выражения |x – a | -длина отрезка координатной оси, соединяющей точки с абсцисами а и х . Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздких решений.
Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованием геометрической интерпритации модуля.
Будем рассуждать следующим образом: исходя из геометрической интерпри-тации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2].
Ответ: х [1; 2]
Пример8. Решим уравнение |x – 1| - |x – 2|=1 1 с использованием геометрической интерпритации модуля.
Будем рассуждать аналогично предыдущему примеру, при этом получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно решением данного уравнения будет являтся не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси ОХ.
Ответ: х [2; +)
Обобщением вышеприведенных уравнений являются следующие равносильные переходы:
|x – a| + |x – b|=b – a, где b a a x b
|x – a| - |x – b|=b – a, где b a x b
4.3. Графики простейших функций, содержащих знак абсолютной величиныПод простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): "Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна -- произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя -- с абсциссой, большей большего из корней.
Например:
1)f(x)=|x - 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1)
2) f(x)=|x - 1| + |x – 2| Вычисляя значение функиции в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых.(рис.2)
3) f(x)=|x - 1| + |x – 2| + |x – 3| Для построения графика вычислим значения функции в точках 1, 2, 3, 0 и 4 (рис.3)
4) f(x)=|x - 1| - |x – 2| График разности строится аналогично графику суммы, тоесть по точкам 1, 2, 0 и 3.
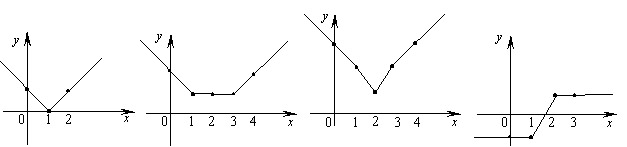
рис1. рис2. рис3. рис4.
4.4.Решение нестандартных уравнений, содержащих модули.Пример9. Решить уравнение 3| x + 2 | + x2 + 6x + 2 = 0.
Решение.
Рассмотрим два случая.
Ответ: (– 4; – 1).
Пример10. Решить уравнение | 4 – x | + | (x – 1)(x – 3) | = 1.
Решение.
Учитывая, что | 4 – x | = | x – 4 |, рассмотрим четыре случая.
 так как
так как ![]()
2)
3)
4) 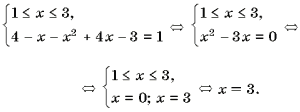
4) 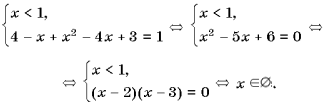
Ответ: 3.
Графический способ.
Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 |
1)в Гy = |(x–1)(x–3)| подставим значение х=1 и х=3. Мы получим у=0,
тоесть пересечение графика с осью ОХ. При х равном нулю у=3, тоесть график пересекается с осью ОУ в точке (0 ;3). И при х=4 у также равен 3- мы получили первый график.
2) y=1–|x–4 | Найдем пересечение с осью ОХ, для этого решим простое уравнение: 1-|x-4|=0
|x-4|=1
x - 4=1 или x - 4=-1
x=5 x=3
Следовательно данный график пересекает ось ОХ в точках 5 и 3.
При х=4 у=1 и ак видно из графика: графики обеих функций пересекаются в одной точке 3
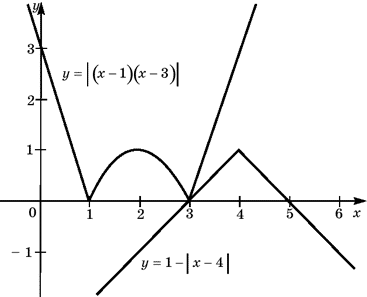
Ответ: 3
Пример11. Решить уравнение | x2 + 3x | = 2(x + 1).
Решение.
Уравнение равносильно системе
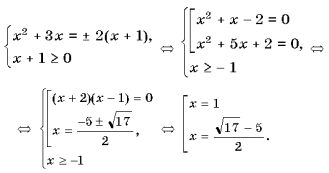
Ответ: 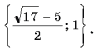
Пример12.Решить уравнение х2 - 4х +|x - 3| +3=0
Для освобождения от знака абсолютной величины разобьем числовую прямую на две области и будем искать решения исходного уравнения в каждой из этих областей отдельно:
__________x 3__________________|____________x<3_________________
|x – 3|=x – 3 |x – 3|=-x + 3
x2 - 4x + x – 3 + 3=0 x2 – 4x – x + 3 + 3=0
x2 – 3x=0 x2 – 5x + 6=0
x(x – 3)
x1=0 или x2=3 D=25 – 4 6=1> 0два различ. корня
x=0 –посторонний корень, так как x1= (5- 1 )/2 =2
не удовлетворяет промежутку. x2=(5 + 1)/2=3
x=3 - посторонний корень, так как
не удовлетворяет промежутку.
Значит, исходное уравнение имеет два решения х1=2 и х2=3
Ответ: х1=2, х2=3
Пример13. Решить уравнение | 2x + 8 | – | x – 5 | = 12.
Решение.
Раскрытие пары модулей приводит к трем случаям (без x + 4 0, x – 5 0).

Ответ: {– 25; 3}.
Пример 14. Решить уравнение .
![]()
Решение:
Напишем равносильную смешанную систему:
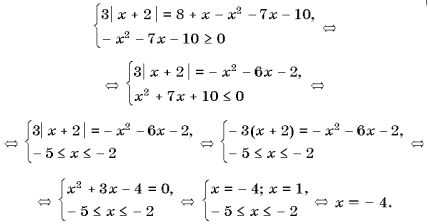
Ответ: х=-4
Пример 15 Решить графически уравнение |1 – x| - |2x + 3| + x + 4=0
Решение:
Представим уравнение в виде |1 – x| - |2x + 3| =-х – 4
Построим два графика у=|1 – x| - |2x + 3| и у=-х – 4
1) у=|1 – x| - |2x + 3|
Критические точки: х=1, х=-1.5
(1 – х) ________+________|______ +____________|_____-______ >
(2х +3) - -1.5 + 1 +
а) х< -1.5, (1– x)>0 и (2х + 3)<0, т.е функция примет вид у=1 – х + 2х + 3,
у=х + 4 –графиком является прямая, проходящая через две точки (0; 4), (-4; 0)
б)При -1.5 x <1, (1 – х)>0 и (2x +3) 0, т.е функция примет вид
у=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через две точки (0; -2), (-1; 1).
в)При х1, (1 – х)0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х – 3,
у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4),
(-4; 0).
График функции у= - х – 4 совпадает с графиком у=|1 – x| - |2x + 3|, при х1,
Поэтому решением являются все х1 и х= -4
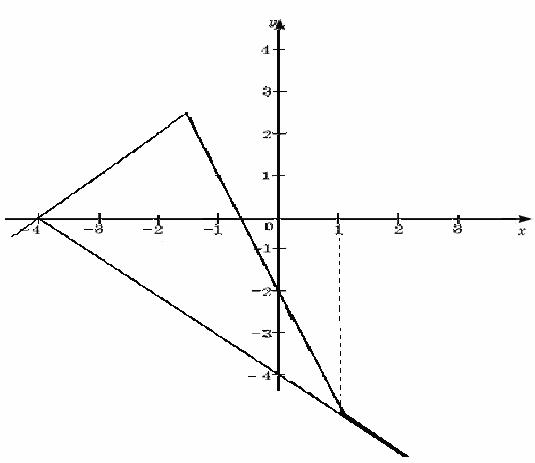
Ответ: х1,х= -4
Аналитическое решение.
y=|1 – x| - |2x + 3|
y=-x – 4
Построим числовую прямую так, чтобы по определению модуля знак абсолютной величины числа можно будет снять. Для этого найдем критические точки: 1- х=0 и 2х – 3 =0,
х=1 х=-1,5
___________х<-1,5_____|_______-1,5 x <1_____|_________x 1__________
|1 – x|=1 – x |1 – x|=1 – x |1 – x|=-1 + x
|2x + 3|=-2x – 3 |2x + 3|=2x + 3 |2x + 3|=2x + 3
1 – x + 2x + 3 + x + 4=0 1 – x – 2x – 3 + x +4=0 -1 + x – 2x – 3 + x + 4=0
2x=-8 -2x=-2 0x=0
x=-4 x=1 x – любое число.
Удовлетворяет данному Не удовлетворяет x [1; + )
промежутку является данному промежут- x 1 корень уравнения
корнем уравнения. куне является кор-
нем уравнения.
Объеденив данные промежутки, получим, что решением данного уравнения являются: x=-4 и x 1
Ответ: x=-4, x 1
5. Заключение.И в заключении я хотел бы сказать, что для досканального изучения материала исследовательская работа подходит лучше всего. Мне представилась возможность больше поработать с интерестной, для меня, темой модуля и выйти за рамки того материала, который предоставляет нам учебник 10-го класса. Прочитав и изучив другую литературу, я узнал много нового и, как я считаю, важного для меня.
Список литературыУчебник математики для Х класса - К. Вельскер, Л. Лепманн,Т. Лепманнн.
2.Уравнения и неравенства – Башмаков М. И.
3.Задачи всесоюзных математических олимпиад-Васильев Н.Б., Егоров А.А.
4.Задачи вступительных экзаменов по математике- Нестеренко Ю.В.,
Олехник С.Н., Потапов
Похожие работы
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих ...
... ;[0; 1), тогда x – x +1 = 1; 1 = 1 Þ x — любое число из [0; 1). В) x Î[1; ¥), тогда x + x – 1 = 1; 2x = 2; x = 1 Î[1; ¥). Ответ: x Î[0; 1]. Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
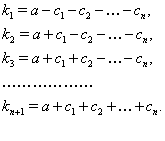
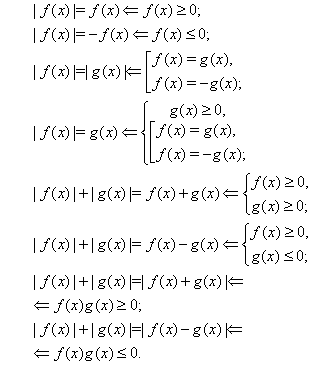
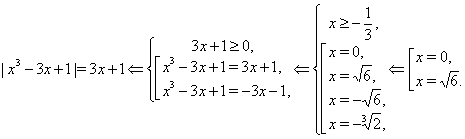


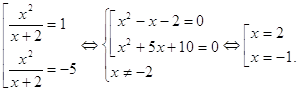
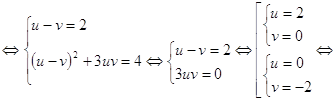
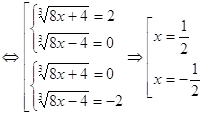
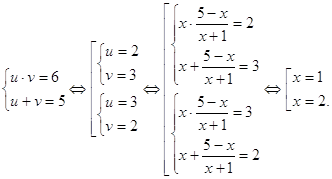
0 комментариев