Навигация
Исследование неоднородной нестационарной сети случайного доступа с динамическим протоколом в условиях перегрузки
2. Исследование неоднородной нестационарной сети случайного доступа с динамическим протоколом в условиях перегрузки
|
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
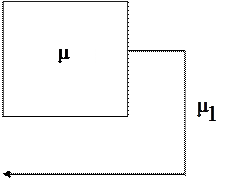
Рис. 2.1 – Модель системы массового обслуживания
В нестационарном режиме распределение
![]()
удовлетворяют системе дифференциально-разностных уравнений вида
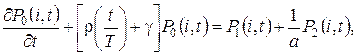
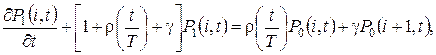 (2.1)
(2.1)
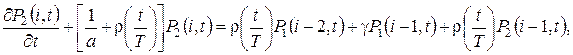
где 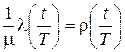 ,
, ![]() ,
, 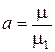 ,
, ![]() .
.
Замечание: система уравнений (2.1) получена аналогично системе уравнений (1.1). Вероятности переходов для состояний системы совпадают с точностью до замены 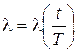 .
.
Систему (2.1) будем решать в условиях перегрузки, то есть при ![]() .
.
Первое приближение
В системе уравнений (2.1) произведем замену переменных: ![]() . В результате такой замены производится переход от дискретной переменной
. В результате такой замены производится переход от дискретной переменной ![]() к непрерывной переменной
к непрерывной переменной ![]() , от t перешли к
, от t перешли к ![]() , причем
, причем ![]() такое, что
такое, что ![]() . После замены производная равна
. После замены производная равна ![]() .
.
Тогда уравнения (2.1) перепишем
![]()
![]() (2.2)
(2.2)
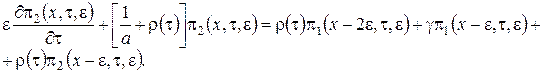
Решим систему уравнений (2.2) в два этапа.
1 этап. Считая ![]() и предполагая, что
и предполагая, что ![]() будем иметь
будем иметь
![]()
![]() (2.3)
(2.3)
![]() .
.
Выразим ![]() через функцию
через функцию 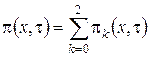 и получим
и получим
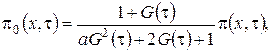
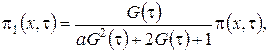 (2.4)
(2.4)
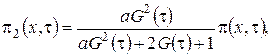
где ![]()
![]() асимптотическая плотность распределения нормированного числа заявок в источнике повторных вызовов.
асимптотическая плотность распределения нормированного числа заявок в источнике повторных вызовов.
Обозначим
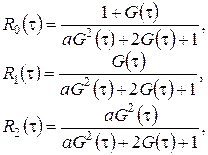 (2.5)
(2.5)
(![]() - это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Заметим, что из системы (2.3) следуют равенства связывающие
- это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Заметим, что из системы (2.3) следуют равенства связывающие ![]() ,
, ![]() и
и ![]()
![]()
![]() (2.6)
(2.6)
![]() .
.
Найдем вид функции ![]() , для этого перейдем ко второму этапу.
, для этого перейдем ко второму этапу.
2 этап. В системе дифференциальных уравнений (2.2) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка ![]() , получим
, получим
![]()
![]() (2.7)
(2.7)
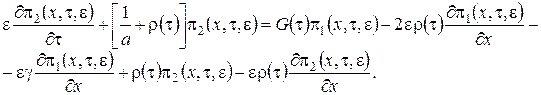
Просуммируем левые и правые части уравнений системы (2.7) и получим равенство
![]() . (2.8)
. (2.8)
С учетом того, что
![]()
равенство (2.8) принимает вид
![]() . (2.9)
. (2.9)
Уравнение (2.9) является однородным линейным уравнением с частными производными первого порядка. Для того чтобы его решить составим уравнение
 ,
,
его решение 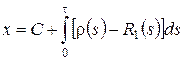 , тогда
, тогда 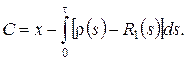
Общее решение уравнения (2.9) имеет вид
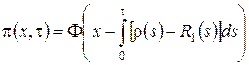 , (2.10)
, (2.10)
где ![]() - произвольная дифференцируемая функция, аналитическое выражение которой найдем из начальных условий.
- произвольная дифференцируемая функция, аналитическое выражение которой найдем из начальных условий.
Пусть распределение в начальный момент времени ![]() где
где ![]() некоторая плотность распределения. Тогда
некоторая плотность распределения. Тогда ![]() следовательно
следовательно 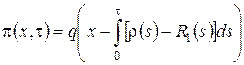 . Возьмем в качестве начальной плотности распределения
. Возьмем в качестве начальной плотности распределения ![]() , где
, где ![]() - дельта-функция Дирака, а
- дельта-функция Дирака, а ![]() ,
, ![]() - число заявок в источнике повторных вызовов в начальный момент времени.
- число заявок в источнике повторных вызовов в начальный момент времени.
Таким образом 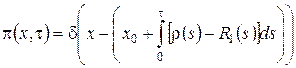 , из свойств функции Дирака следует, что
, из свойств функции Дирака следует, что 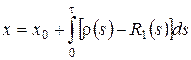 .
.
То есть мы получили, что ![]() ,
, ![]() имеет смысл асимптотического среднего.
имеет смысл асимптотического среднего.
Из приведенных рассуждений вытекает еще одно важное следствие, а именно
![]() имеет место
имеет место ![]() , тогда
, тогда ![]() (отрицательная функция
(отрицательная функция ![]() противоречит смыслу задачи). В нашем случае
противоречит смыслу задачи). В нашем случае ![]() совпадает с пропускной способностью системы.
совпадает с пропускной способностью системы.
Перейдем ко второму приближению, в котором будем искать распределение отклонения от асимптотического среднего.
Второе приближение
В исходной системе уравнений (2.1) сделаем замену переменных ![]() .
.
Заметим, что в новых обозначениях производная по времени ![]() равна
равна 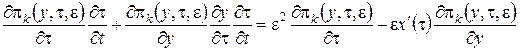 . С учетом этого система (2.1) примет вид
. С учетом этого система (2.1) примет вид
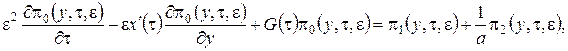
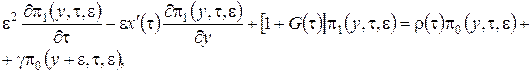 (2.11)
(2.11)
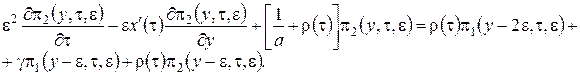
Решение системы уравнений (2.11) аналогично решению системы (2.2), но проводится в три этапа.
1 этап. В системе дифференциальных уравнений (2.13) сделаем предельный переход при ![]() и предположим, что
и предположим, что ![]() , получим
, получим
![]()
![]() (2.12)
(2.12)
![]() .
.
Решим эту систему аналогично тому, как решили систему уравнений (2.3). Введем функцию 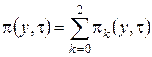 и выразим через нее
и выразим через нее ![]() , получим
, получим
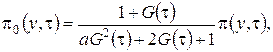
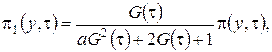 (2.13)
(2.13)

где ![]() асимптотическая плотность распределения отклонения числа заявок в источнике повторных вызовов от асимптотического среднего.
асимптотическая плотность распределения отклонения числа заявок в источнике повторных вызовов от асимптотического среднего.
2 этап. Функции ![]() будем искать с точностью до
будем искать с точностью до ![]() в форме
в форме
![]() (2.14)
(2.14)
Найдем вид функций ![]() ,
, ![]() и
и ![]() . Для этого в системе дифференциальных уравнений (2.11) все функции с аргументом
. Для этого в системе дифференциальных уравнений (2.11) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничимся слагаемыми порядка
, ограничимся слагаемыми порядка ![]() . Получим
. Получим
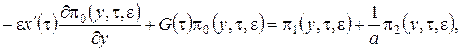
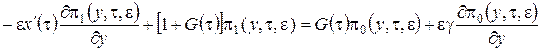 (2.15)
(2.15)
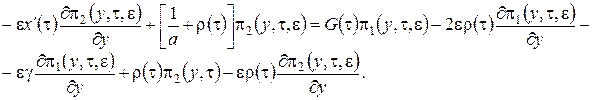
В уравнения (2.15) подставим ![]() в форме (2.14), приведем подобные и получим систему неоднородных линейных алгебраических уравнений относительно
в форме (2.14), приведем подобные и получим систему неоднородных линейных алгебраических уравнений относительно ![]() вида
вида
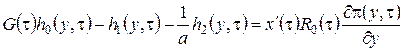 ,
,
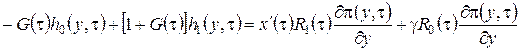 ,
(2.16)
,
(2.16)
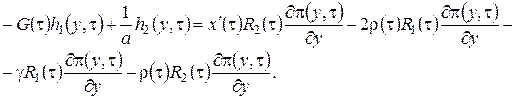
Нетрудно увидеть, что между уравнениями этой системы есть зависимость и ранг матрицы системы равен, следовательно, чтобы решение уравнений (2.16)существовало, необходимо выполнение равенства
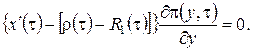 (2.17)
(2.17)
Из однородного линейного уравнения с частными производными первого порядка (2.9) мы знаем, что ![]() . Таким образом, можно сделать вывод, что система (2.16) разрешима. При условии, что функция
. Таким образом, можно сделать вывод, что система (2.16) разрешима. При условии, что функция ![]() известна, решение можно записать в виде
известна, решение можно записать в виде
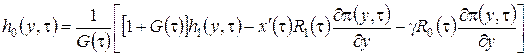 ,
,
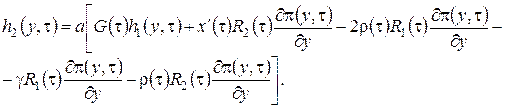 (2.18)
(2.18)
Теперь все готово, для того, чтобы найти функцию ![]() . Перейдем к третьему этапу.
. Перейдем к третьему этапу.
3 этап. В системе дифференциальных уравнений (2.11) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка ![]() , получим
, получим
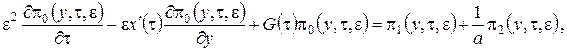
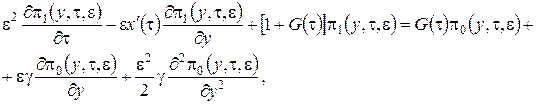 (2.19)
(2.19)
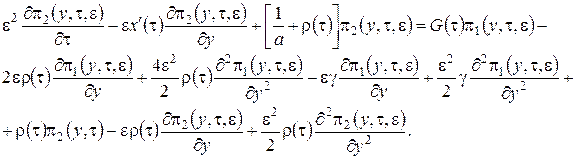
Теперь подставим в уравнения (2.19) ![]() в форме (2.14) и просуммируем левые и правые части уравнений, будем иметь
в форме (2.14) и просуммируем левые и правые части уравнений, будем иметь
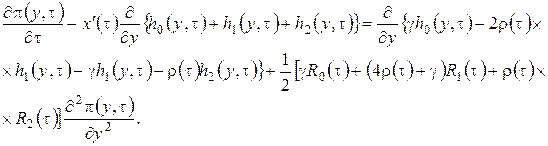 (2.20)
(2.20)
Подставляя вместо ![]() и
и ![]() их выражения, полученные на втором этапе получим для
их выражения, полученные на втором этапе получим для ![]() уравнение Фоккера-Планка
уравнение Фоккера-Планка
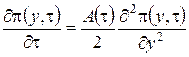 ,
(2.21)
,
(2.21)
где
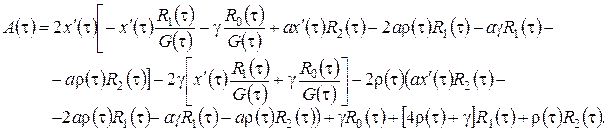
Нормированным решением полученного одномерного уравнения диффузии [8] является плотность нормального распределения вероятностей с нулевым средним и дисперсией
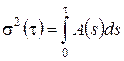 .
(2.22)
.
(2.22)
3. Исследование нестационарной сети случайного доступа со статическим протоколом в условиях большой задержки
Исследуем сеть связи, функционирование которой изложено в разделе 1, в условиях большой задержки. В этом случае удобнее рассматривать случай, когда интенсивность каждой заявки в ИПВ равна ![]() . Структура такой СМО имеет вид рис. 3.1.
. Структура такой СМО имеет вид рис. 3.1.
 | ||||||||||||
 | ||||||||||||
 | ||||||||||||
Рис. 3.1 – Модель системы массового обслуживания
Вероятности переходов из состояния системы ![]() в произвольный момент времени t в состояние
в произвольный момент времени t в состояние ![]() за бесконечно малый интервал времени
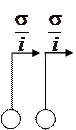
за бесконечно малый интервал времени ![]() показаны на рис. 3.2, рис. 3.3, рис. 3.4.
показаны на рис. 3.2, рис. 3.3, рис. 3.4.
Выпишем уравнения статистического равновесия для нестационарного распределения процесса ![]() , описывающего функционирование сети
, описывающего функционирование сети
![]()
![]() (3.1)
(3.1)
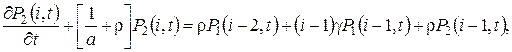
где 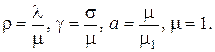
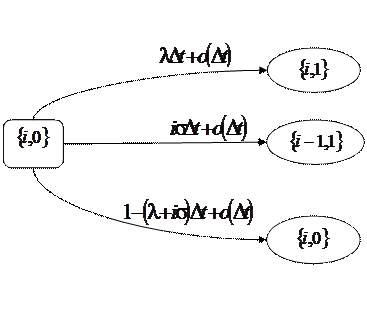
Рис. 3.2 – Возможные переходы из состояния ![]()
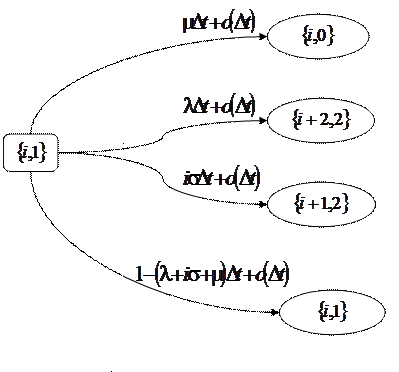
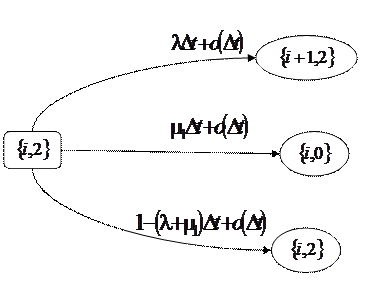 Рис. 3.3 – Возможные переходы из состояния
Рис. 3.3 – Возможные переходы из состояния ![]()
Рис. 3.4 – Возможные переходы из состояния ![]()
Найти точное аналитическое решение системы (3.1) практически невозможно, но можно решить асимптотически в условиях большой задержки, то есть при ![]() .
.
Первое приближение
Для асимптотического решения системы (3.1) сделаем замену переменных ![]() . В результате замены производится переход от дискретной переменной
. В результате замены производится переход от дискретной переменной ![]() к непрерывной переменной
к непрерывной переменной ![]() .
.
В новых обозначениях ![]() . Тогда система (3.1) примет вид
. Тогда система (3.1) примет вид
![]()
![]() (3.2)
(3.2)
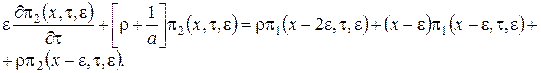
Получим вид решения системы (3.2), которую будем решать в два этапа.
1 этап. Считая ![]() и предполагая, что
и предполагая, что ![]() , будем иметь
, будем иметь
![]()
![]() (3.3)
(3.3)
![]() .
.
Выразим ![]() через функцию
через функцию 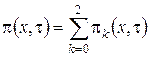 и получим
и получим
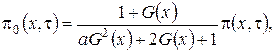
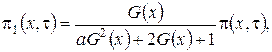 (3.4)
(3.4)
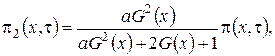
где ![]()
![]() - асимптотическая плотность нормированного числа заявок в источнике повторных вызовов.
- асимптотическая плотность нормированного числа заявок в источнике повторных вызовов.
Обозначим
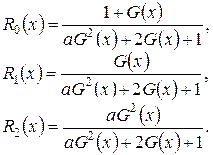 (3.5)
(3.5)
Заметим, что из системы (3.3) следуют равенства
![]()
![]() (3.6)
(3.6)
![]() .
.
Осталось найти вид функции ![]() . Для этого перейдем ко второму этапу.
. Для этого перейдем ко второму этапу.
2 этап. В системе (3.2) разложим функции по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка ![]() , получим систему
, получим систему
![]()
![]() (3.7)
(3.7)
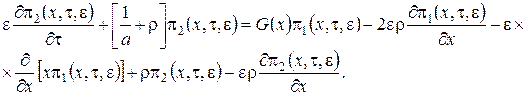
Просуммируем полученные уравнения, поделим на ![]() и перейдем
и перейдем ![]() . Тогда будем иметь
. Тогда будем иметь
![]() . (3.8)
. (3.8)
С учетом того, что
![]()
равенство (3.8) принимает вид
![]() . (3.9)
. (3.9)
Таким образом мы получили, что ![]() удовлетворяет уравнению Фоккера-Планка с коэффициентом переноса равным
удовлетворяет уравнению Фоккера-Планка с коэффициентом переноса равным ![]() , и нулевым коэффициентом диффузии. Из определения для коэффициента переноса можно сделать вывод, что
, и нулевым коэффициентом диффузии. Из определения для коэффициента переноса можно сделать вывод, что ![]() , то есть
, то есть ![]() зависит от времени и
зависит от времени и ![]() – имеет смысл асимптотического среднего, в ее окрестности достаточно долго флуктуируют значения нормированного процесса
– имеет смысл асимптотического среднего, в ее окрестности достаточно долго флуктуируют значения нормированного процесса ![]() .
.
Второе приближение
Зная асимптотическое среднее, найдем распределение вероятностей значений отклонения ![]() от его среднего. Для этого в исходной системе уравнений (3.1) сделаем замену переменных
от его среднего. Для этого в исходной системе уравнений (3.1) сделаем замену переменных ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
В новых обозначениях производная ![]() равна
равна 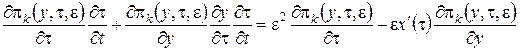 .
.
Будем иметь
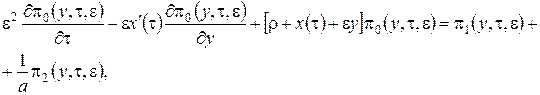
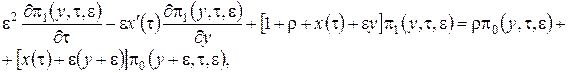 (3.10)
(3.10)
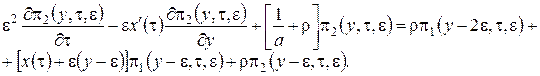
Решение системы (3.10) аналогично решению системы (3.2), но проводится в три этапа.
1 этап. В системе дифференциальных уравнений (3.10) положим ![]() и найдем решение в виде
и найдем решение в виде
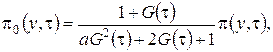
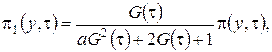 (3.11)
(3.11)

где 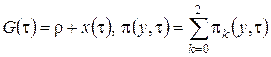 – асимптотическое распределение нормированного числа заявок в источнике повторных вызовов в окрестности асимптотического среднего.
– асимптотическое распределение нормированного числа заявок в источнике повторных вызовов в окрестности асимптотического среднего.
Перейдем ко второму этапу.
2 этап. Неизвестные функции ![]() будем искать с точностью до
будем искать с точностью до ![]() форме
форме
![]() (3.12)
(3.12)
где ![]() имеют вид аналогичный (3.5), где в качестве
имеют вид аналогичный (3.5), где в качестве ![]() выступает
выступает ![]() и для них справедливы равенства (3.7).
и для них справедливы равенства (3.7).
Найдем вид функций ![]() .
.
С точностью до ![]() (3.10) запишем
(3.10) запишем
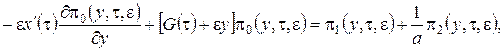
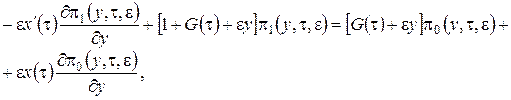 (3.13)
(3.13)
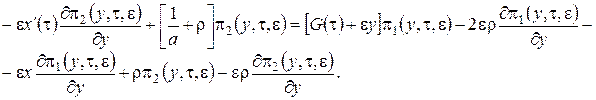
В уравнения (3.13) подставим ![]() в форме (3.12), уничтожим подобные слагаемые и получим систему неоднородных линейных алгебраических уравнений относительно функций
в форме (3.12), уничтожим подобные слагаемые и получим систему неоднородных линейных алгебраических уравнений относительно функций ![]() вида
вида
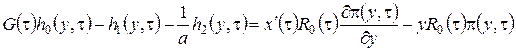 ,
,
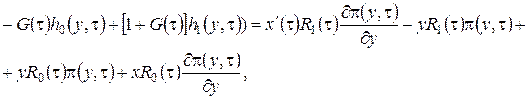 , (3.14)
, (3.14)
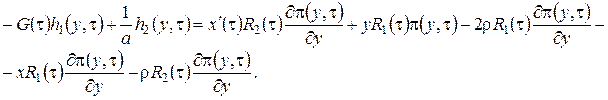
Система (3.14) будет иметь решение, если 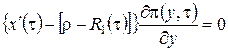 . Из уравнения Фоккера-Планка (3.9) мы знаем, что
. Из уравнения Фоккера-Планка (3.9) мы знаем, что ![]() . Таким образом, можно сделать вывод, что система (3.14) разрешима. При условии, что функция
. Таким образом, можно сделать вывод, что система (3.14) разрешима. При условии, что функция ![]() известна, решение системы (3.14) можно записать так
известна, решение системы (3.14) можно записать так
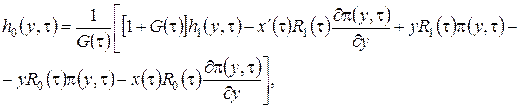 (3.15)
(3.15)
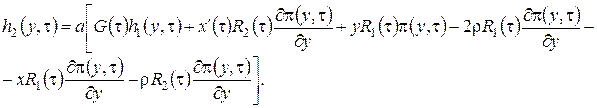
Перейдем к третьему этапу.
3 этап. С точностью до ![]() уравнения (3.10) запишем следующим образом
уравнения (3.10) запишем следующим образом
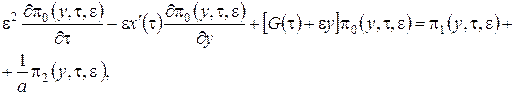
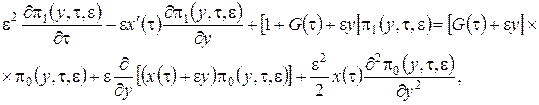 (3.16)
(3.16)
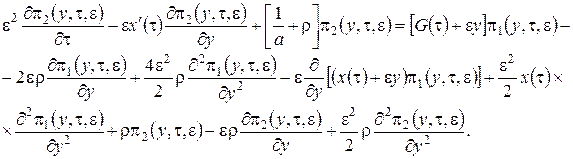
Теперь подставляем в систему уравнений (3.16) ![]() в форме (3.12), оставляем слагаемые, имеющие порядок не выше
в форме (3.12), оставляем слагаемые, имеющие порядок не выше ![]() и суммируем уравнения. Получим равенство для нахождения
и суммируем уравнения. Получим равенство для нахождения ![]()
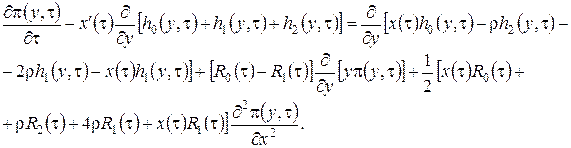 (3.17)
(3.17)
В полученное равенство подставим выражения для функции ![]() и
и ![]() , найденные на втором этапе. В результате приведения подобных, для
, найденные на втором этапе. В результате приведения подобных, для ![]() получим уравнение Фоккера-Планка
получим уравнение Фоккера-Планка
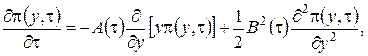 (3.18)
(3.18)
с коэффициентом переноса  и коэффициентом диффузии
и коэффициентом диффузии
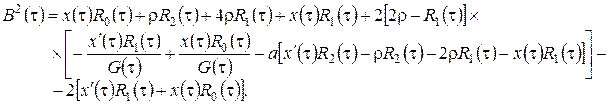
Уравнение Фоккера-Планка (3.18) получено для некоторого диффузионного процесса ![]() , плотность распределения вероятностей которого
, плотность распределения вероятностей которого ![]() .
.
Запишем стохастическое дифференциальное уравнение для ![]() в общей форме
в общей форме
![]() ,
(3.19)
,
(3.19)
где ![]() - винеровский процесс с нулевым средним и единичным коэффициентом диффузии, в нашем случае оно приобретает вид
- винеровский процесс с нулевым средним и единичным коэффициентом диффузии, в нашем случае оно приобретает вид
![]() . (3.20)
. (3.20)
Введем новый случайный процесс ![]() ,
(3.21)
,
(3.21)
для его приращения справедливо
![]()
Выберем функцию ![]() так, чтобы она удовлетворяла дифференциальному уравнению
так, чтобы она удовлетворяла дифференциальному уравнению ![]() . Например,
. Например, 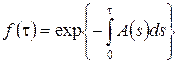 . Тогда
. Тогда ![]() и, следовательно,
и, следовательно, 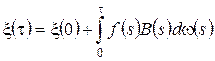 .
.
Выразим из (3.21) функцию ![]() (заметим, что
(заметим, что ![]() ) и получим
) и получим
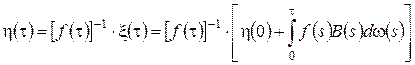 (3.22)
(3.22)
Анализируя вид процесса ![]() можно сделать вывод, что он распределен по нормальному закону. Найдем
можно сделать вывод, что он распределен по нормальному закону. Найдем ![]() и
и ![]() , которые полностью определяют вид плотности распределения
, которые полностью определяют вид плотности распределения ![]() . Учитывая свойства винеровского процесса, получим
. Учитывая свойства винеровского процесса, получим
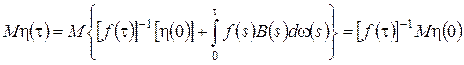 (3.23)
(3.23)
Найдем дисперсию.
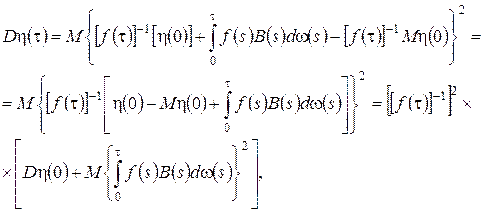
рассмотрим второе слагаемое подробнее. Для этого введем обозначение ![]() , тогда получим
, тогда получим
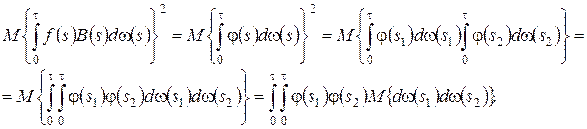
С учетом того, что ![]() будем иметь
будем иметь
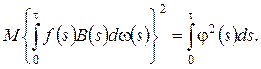
Тогда в окончательном варианте дисперсия равна
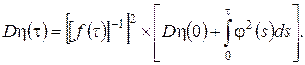 (3.24)
(3.24)
Теперь можно записать решение уравнения Фоккера-Планка (3.18), которое имеет вид
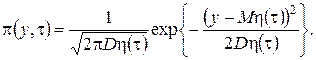 (3.25)
(3.25)
Пусть ![]() , где
, где ![]() - точка покоя дифференциального уравнения
- точка покоя дифференциального уравнения ![]() , которая определяется конечным уравнением
, которая определяется конечным уравнением
![]() , (3.26)
, (3.26)
где 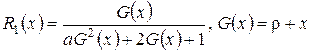 .
.
Возможны три варианта:
1. ![]() , тогда точек покоя не существует (рис. 3.5).
, тогда точек покоя не существует (рис. 3.5).
2. ![]() , тогда существует одна точка покоя
, тогда существует одна точка покоя ![]() .
.
3. ![]() , тогда существует две точки покоя
, тогда существует две точки покоя ![]() и
и ![]() .
.
Для примера рассмотрим случай, когда ![]() (рис. 3.6). Тогда уравнение (3.26) имеет единственный корень
(рис. 3.6). Тогда уравнение (3.26) имеет единственный корень ![]() . Коэффициенты диффузии уравнения Фоккера-Планка не зависят от времени и равны
. Коэффициенты диффузии уравнения Фоккера-Планка не зависят от времени и равны ![]() . Если взять
. Если взять ![]() , то уравнение (3.26) будет иметь два корня
, то уравнение (3.26) будет иметь два корня ![]() и
и ![]() (рис. 3.7). Для первой точки коэффициенты диффузии равны
(рис. 3.7). Для первой точки коэффициенты диффузии равны ![]() , для второй
, для второй ![]() . Точка
. Точка ![]() является нежелательной. Если предположить, что сеть связи работает в стационарном режиме, то в окрестности точки
является нежелательной. Если предположить, что сеть связи работает в стационарном режиме, то в окрестности точки ![]() распределение нормированного числа заявок в ИПВ является нормальным [1] и имеет вид
распределение нормированного числа заявок в ИПВ является нормальным [1] и имеет вид
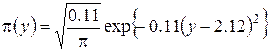 , (3.27)
, (3.27)
| |||
|
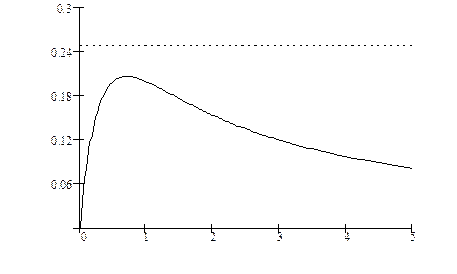
Рис. 3.5
![]()
|
|
|

Рис. 3.6
![]()
|
|
|
|

Рис. 3.7
Похожие работы
... исполнители высокой квалификации; это вполне может быть осуществлено в короткие сроки силами службы эксплуатации. Использование вторичных энергоресурсов для нагрева теплоносителей в системах отопления, вентиляции и кондиционирования воздуха. Использование вторичных энергоресурсов (ВЭР) для теплоснабжения промышленных зданий приобретает все большие масштабы. Экономически это вполне оправдано – ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...


0 комментариев