Навигация
Определение области применимости асимптотических формул по результатам численного анализа
4.3. Определение области применимости асимптотических формул по результатам численного анализа
Таким образом, исходная система уравнений (4.1), описывающая состояние исследуемой сети связи, была исследована численно и аналитически с использованием асимптотического метода.
Численное решение дает точное решение системы, то есть позволяет точно определить распределение вероятностей ![]() исследуемой величины
исследуемой величины ![]() . Для различных параметров системы
. Для различных параметров системы ![]() наблюдается качественное отличие результатов численного исследования исходной системы. Объяснить это, используя только численный метод, очень сложно.
наблюдается качественное отличие результатов численного исследования исходной системы. Объяснить это, используя только численный метод, очень сложно.
Сравнение результатов численного и аналитического исследования для небольших N продемонстрировано на рис. 4.2 и рис. 4.3. С ростом N тенденция поведения исследуемого процесса ![]() предполагаемая аналитическим исследованием, прослеживается для численного решения системы, то есть аналитические выкладки подтверждаются точным численным решением системы (рис. 4.4, рис. 4.5, рис. 4.6). Доказательством неплохого совпадения результатов исследований служат таблицы вероятностно-временных характеристик системы.
предполагаемая аналитическим исследованием, прослеживается для численного решения системы, то есть аналитические выкладки подтверждаются точным численным решением системы (рис. 4.4, рис. 4.5, рис. 4.6). Доказательством неплохого совпадения результатов исследований служат таблицы вероятностно-временных характеристик системы.
Вероятностно-временные характеристики:
1. ![]() – среднее число требований в системе, определяется по формуле
– среднее число требований в системе, определяется по формуле
 (4.35)
(4.35)
или ![]() , (4.36)
, (4.36)
где ![]() – асимптотическое среднее величины
– асимптотическое среднее величины ![]() .
.
Формула (4.35) используется при численном исследовании, при аналитическом исследовании используется формула (4.36).
2. ![]() – среднее число требований, обращающихся к прибору в единицу времени, где за единицу времени выбрано среднее время обслуживания одного требования. Для определения
– среднее число требований, обращающихся к прибору в единицу времени, где за единицу времени выбрано среднее время обслуживания одного требования. Для определения ![]() используется формула
используется формула
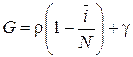 ,
(4.37)
,
(4.37)
где ![]() определяется по формуле (4.35) или (4.36) в зависимости от метода исследования.
определяется по формуле (4.35) или (4.36) в зависимости от метода исследования.
3. ![]() – среднее число попыток до успешной передачи сообщения, определятся по формуле
– среднее число попыток до успешной передачи сообщения, определятся по формуле
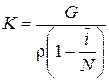 . (4.38)
. (4.38)
4. ![]() – среднее время доставки сообщения, по теореме Литла определяется по формуле
– среднее время доставки сообщения, по теореме Литла определяется по формуле
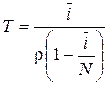 .
(4.39)
.
(4.39)
5. ![]() – производительность сети, определяется по формуле
– производительность сети, определяется по формуле
![]() . (4.40)
. (4.40)
6.![]() – вероятность успешной передачи сообщения с нулевым временем ожидания, определяется по формуле
– вероятность успешной передачи сообщения с нулевым временем ожидания, определяется по формуле
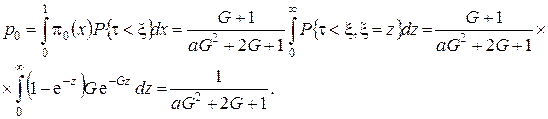 (4.41)
(4.41)
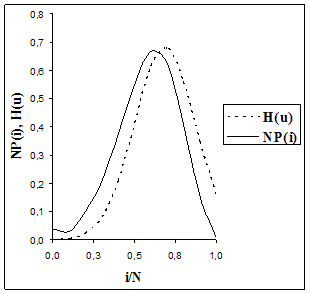
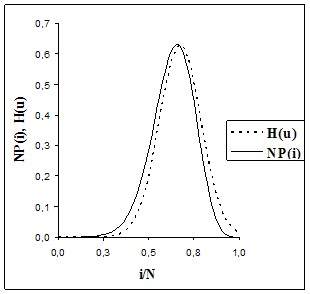
Рис. 4.2:![]() Рис. 4.3:
Рис. 4.3: ![]()
Таблица 1. Вероятностно-временные характеристики
| Хар-ки |
|
| ||
| Метод | Метод | |||
| Точный | Асимптотический | Точный | Асимптотический | |
|
| 5,76 | 6,85 | 19,07 | 20,23 |
|
| 0,921 | 0,85 | 0,669 | 0,65 |
|
| 3,339 | 4,145 | 3,673 | 3,99 |
|
| 0,021 | 0,033 | 0,105 | 0,124 |
|
| 0,276 | 0,205 | 0,182 | 0,163 |
|
| 0,22 | 0,241 | 0,242 | 0,251 |
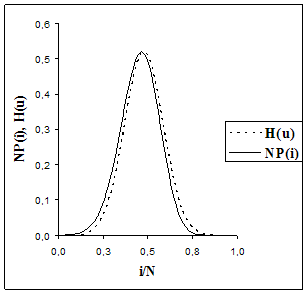
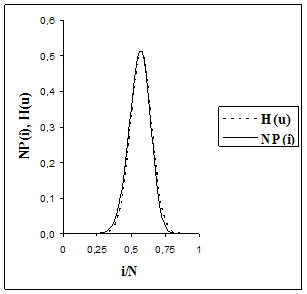
Рис. 4.4:![]() Рис. 4.5:
Рис. 4.5: ![]()
Таблица 2. Вероятностно-временные характеристики
| Хар-ки |
|
| ||
| Метод | Метод | |||
| Точный | Асимптотический | Точный | Асимптотический | |
|
| 22,69 | 23,87 | 55,2 | 56,3 |
|
| 0,608 | 0,6 | 0,703 | 0,7 |
|
| 3,182 | 3,28 | 5,233 | 5,34 |
|
| 0,119 | 0,13 | 0,411 | 0,43 |
|
| 0,191 | 0,183 | 0,134 | 0,131 |
|
| 0,3 | 0,304 | 0,186 | 0,187 |
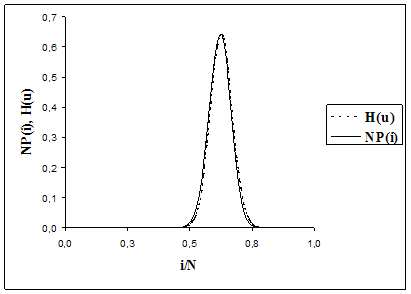
Рис. 4.6:![]()
Таблица 3. Вероятностно- временные характеристики для сети связи с параметрами ![]()
| Хар-ки | Метод | |
| Точный | Асимптотический | |
|
| 124,05 | 125,28 |
|
| 0,603 | 0,6 |
|
| 2,889 | 2,92 |
|
| 0,594 | 0,61 |
|
| 0,209 | 0,205 |
|
| 0,341 | 0,342 |
Таким образом, используя полученную информацию об исследовании системы, мы можем управлять ее функционированием, добиваясь нужных нам характеристик путем изменения параметров, влияющих на состояние системы.
Численное исследование позволило установить следующее: в системе, построенной на основе протокола с оповещением о конфликте для конечного числа АС можно пренебречь различием предельной и допредельной моделей.
Заключение
В данной работе проведено исследование функционирования нестационарных сетей связи случайного доступа с оповещением о конфликте для конечного и бесконечного числа абонентских станций. Рассмотрен динамический и статический протокол случайного множественного доступа.
В первом разделе проведено исследование нестационарной сети случайного доступа с динамическим протоколом в условиях большой загрузки. Определена точная верхняя граница загрузки сети, при которой существует стационарный режим. Исследование показало, что плотность распределения нормированного числа заявок в источнике повторных вызовов удовлетворяет уравнению Фоккера-Планка с постоянными коэффициентами. Предложен метод его решения с помощью преобразования Лапласа.
Во втором разделе проведено исследование неоднородной нестационарной сети случайного доступа с динамическим протоколом в условиях перегрузки. В первом приближении получено асимптотическое среднее, во втором распределение отклонения в окрестности асимптотического среднего, которое удовлетворяет уравнению Фоккера-Планка с нулевым коэффициентом переноса и является нормальным.
В третьем разделе проведено исследование нестационарной сети случайного доступа со статическим протоколом в условиях большой задержки. В первом приближении получено асимптотическое среднее, во втором распределение отклонения в окрестности асимптотического среднего, которое удовлетворяет уравнению Фоккера-Планка и является нормальным. Рассмотрены точки покоя.
В четвертом разделе исследовано функционирование сети случайного множественного доступа с динамическим протоколом для конечного числа абонентских станций. В п. 4.1. изложены два этапа асимптотического анализа. На первом этапе удалось определить асимптотическую «предельную» точку, в окрестности которой «концентрируется» искомая плотность распределения вероятности, а на втором этапе – нашли распределение отклонения в окрестности «предельной» точки. На этом этапе получено асимптотически нормальное распределение, что является аналогом известных в теории вероятностей законов больших чисел и центральных предельных теорем. Особенностью рассматриваемой СМО, является то, что алгебраические уравнения, описывающие ее функционирование, имеют точное численное решение, которое изложено в п. 4.2. Поэтому в п. 4.3. проводится аналогия между численным и асимптотическим решением и определяется область применимости асимптотических формул.
Список использованной литературы
1. Радюк Л.Е., Терпугов А. Ф. Теория вероятностей и случайных процессов – учебное пособие. Томск: Издательство Томского университета, 1988.
2. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. М: Наука, 1987.
3. Клейнрок Л. Вычислительные системы с очередями. М: Мир, 1979.
4. Кениг Д., Штоян Д. Методы теории массового обслуживания. М: Радио и связь, 1981.
5. Боровков А. А. Асимптотические методы в теории массового обслуживания. М: Наука, 1980.
6. Гихман И. И., Скороход А. В. Стохастические дифференциальные уравнения. Киев: Наукова думка, 1968.
7. Назаров А. А. Асимптотический анализ марковизируемых систем. Томск: Издательство Томского университета, 1991.
8. Араманович И. Г., Левин В. И. Уравнения математической физики. М: Наука, 1969.
9. Саати Т. Л. Элементы теории массового обслуживания и ее приложения .М: Советское радио, 1971.
10. Климов Г.П. Стохастические системы обслуживания. М: Наука, 1966.
11. Ги К. Введение в локальные вычислительные сети. М: Радио и связь, 1986.
12. Бертсекас Д., Галлагер Р. Сети передачи данных. М: Мир, 1989.
13. Баруча-Рид А. Т. Элементы теории марковских процессов и их приложения. М: Наука, 1969.
14. Шохор С. Л. Математические модели локальных вычислительных сетей с динамическими протоколами случайного множественного доступа и их исследование//Автореферат диссертации. Томск, 2001.
15. Одышев Ю. Д. Исследование сетей связи, управляемых протоколом случайного множественного доступа «Адаптивная АЛОХА»//Автореферат диссертации. Томск, 2001.
16. Туенбаева А. Н. Исследование математических моделей сетей связи со статическими протоколами случайного множественного доступа//Автореферат диссертации. Томск, 2001.
Похожие работы
... исполнители высокой квалификации; это вполне может быть осуществлено в короткие сроки силами службы эксплуатации. Использование вторичных энергоресурсов для нагрева теплоносителей в системах отопления, вентиляции и кондиционирования воздуха. Использование вторичных энергоресурсов (ВЭР) для теплоснабжения промышленных зданий приобретает все большие масштабы. Экономически это вполне оправдано – ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...
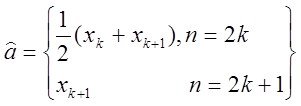


0 комментариев